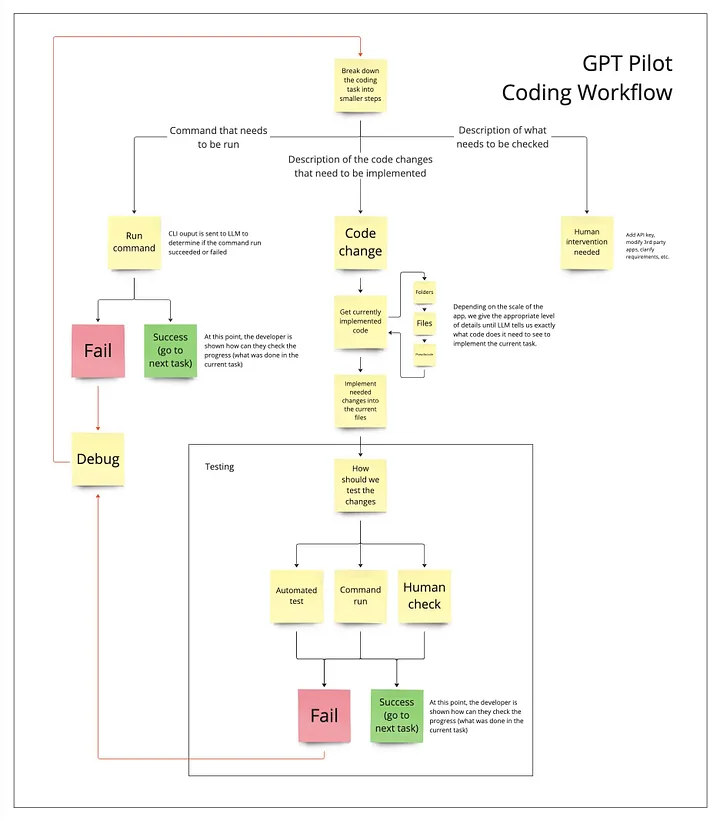
图机器学习（Graph Machine Learning，简称Graph ML）是机器学习的一个分支，专注于利用图形结构的数据。在图形结构中，数据以图的形式表示，其中的节点（或顶点）表示实体，边（或链接）表示实体之间的关系。

本篇文章将从基础开始介绍什么是图，我们如何描述和表示它们，以及它们的属性是什么。

图论是在18世纪由欧拉引入的，用来解决著名的柯尼斯堡大桥问题：是否有可能只穿过七座桥中的每座桥一次。

什么是图?如何定义它?

图就是一组相互连接的对象。

一个图有一组结点N和边E, n是顶点的数目，m是边的数目。连接的两个节点被定义为相邻(节点1相邻或邻接4)。当我们称网络的大小N时，通常指的是节点的数量(链路或边的数量通常称为L)。

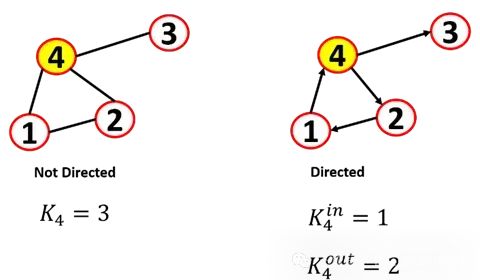
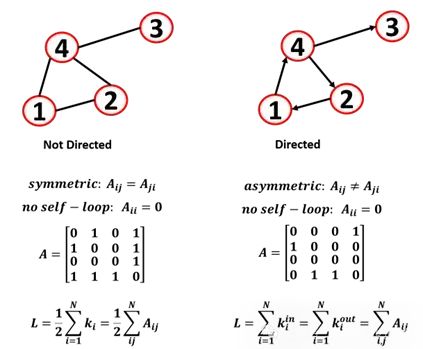
有向与无向

图可以是无向图或有向图:

无向图:边是无向的，关系是对称的。画边的顺序并不重要。

有向图:边是有向的(也称为有向图)，顶点之间的边可以有方向，可以用箭头表示(也称为弧线)。

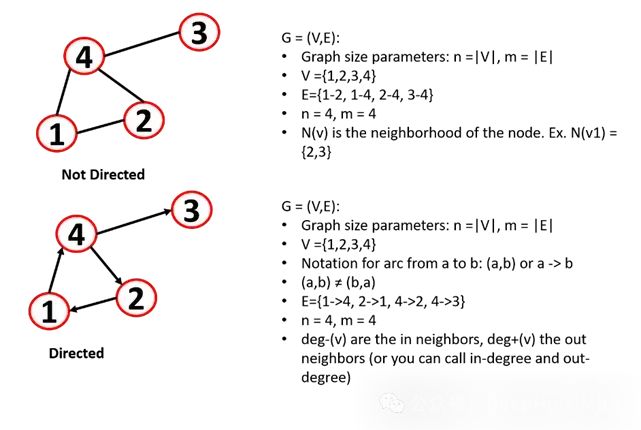
图的基本性质

对于一个节点，我们可以将节点度(k)定义为与节点相邻的边，对于一个图，我们可以计算无向图的平均度k:

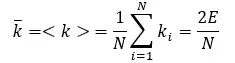
在有向网络中，定义了一个节点的入度(指指向该节点的边)和出度(指离开该节点的边)，节点的总度是两者的和。我们称source节点为没有入度的节点，称sink节点为没有出度的节点。

我们可以计算平均度为:

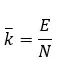
这里的

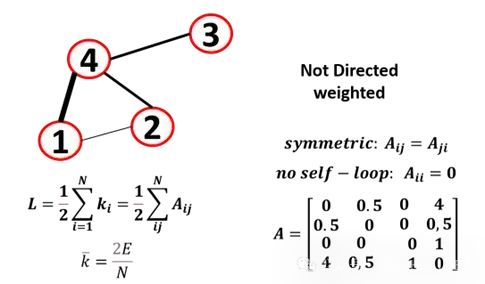
邻接矩阵是表示图的另一种方式，其中行和列表示图节点，交集表示一个节点的两个节点之间是否存在链接。邻接矩阵的大小是n x n(顶点数)。如果Aij是节点i和j之间的链接，则Aij为1，否则为0，对于无向图，矩阵是对称的。可以看到在矩阵的对角线上没有1意味着没有自环(节点与自身相连)

对于一个节点i计算一个节点的边(或它的度)，沿着行或列求和:

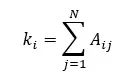
无向图中的总边数是每个节点的度之和(也可以是邻接矩阵中的值之和):

因为在无向图中，你要计算两次边(由于邻接矩阵是对称的，要计算两次相同的边)，所以除以2

对于有向图，可以表示两个不同的邻接矩阵，一个表示入度，一个表示出度

对于一个节点，总边数是入度和出度之和:

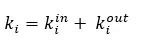
我们计算一个节点的入度和出度以及总边数:

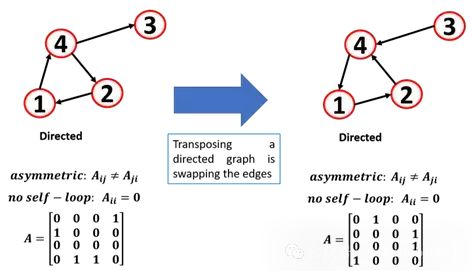
由于线性代数和图论之间存在联系，所以可以对邻接矩阵应用不同的操作。如果转置一个无向图的邻接矩阵，图是没有改变的因为是对称的，但如果转置一个有向图的邻接矩阵，边则进行了方向的转换。

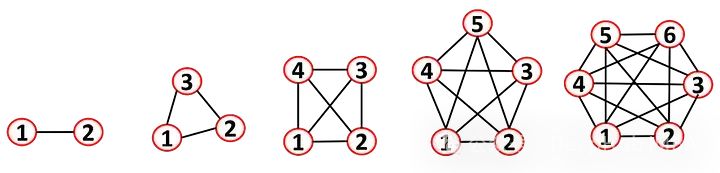
这些矩阵非常是稀疏的，因为理论上一个节点是可以连接到所有其他节点，但这在现实生活中基本上不会发生。当所有节点都与其他节点相连时，我们称之为完全图。完全图通常用于理解图论中的一些复杂问题(连通性例子等)。

图的最大密度是一个完全图中可能关系的总数。实际密度是测量无向非完全图的密度:

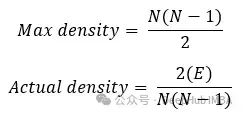
理论上来说在社交网络中，每个人都可以连接到每个人，但这并没有发生。所以最终得到一个70亿行和70亿列的邻接矩阵，其中大多数条目为零(因为非常稀疏)。为什么要说这个呢？因为不是所有的算法都能很好地处理稀疏矩阵。

除了邻接矩阵，我们还可以将图表示为一个边的列表:

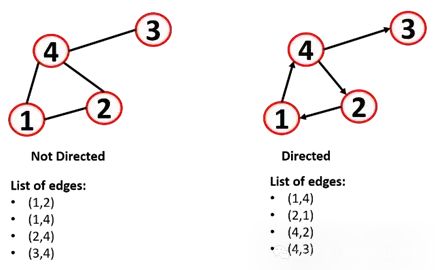
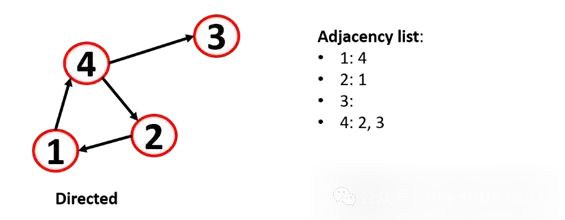
但是这种方法对于机器学习分析是有问题的，所以就出现了一种常用的方法：邻接表，因为邻接表对大型和稀疏的节点很有用，它允许快速检索节点的邻居。

加权图

图边还可以增加权值，边并不都是相同的，比如在交通图中，为了选择两个节点之间的最佳路径，我们将考虑表示时间或交通的权重。

自循环

图的节点是可以连接到自己的，所以必须在计算总边数时添加自循环

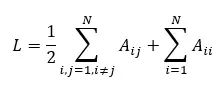
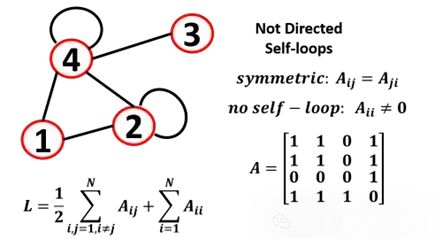
你也可以有一个多图，一个对节点有多条边

多重图

含有平行边的图称为多重图，或者说一个对节点有多条边

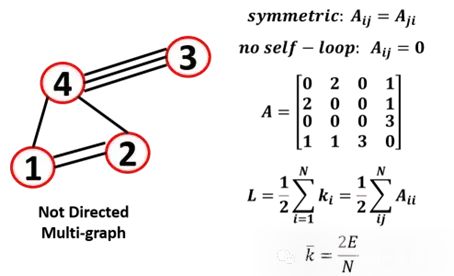
上面就是一些常见的图和表示方式，我们来做一个汇总

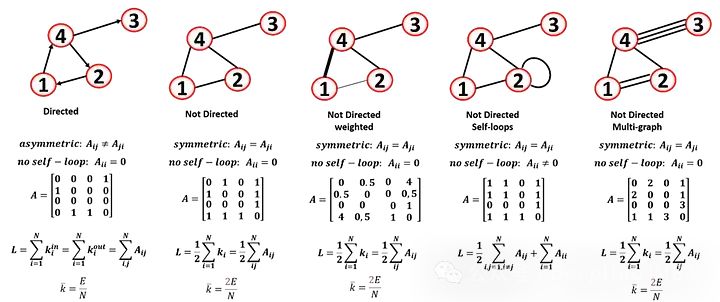
图的另一个重要参数是连接性(连通性)。每个节点都能被所有其他节点到达吗?连通图是指所有顶点都可以通过一条路径连接起来的图。不连通图是指有两个或多个连通分量的图

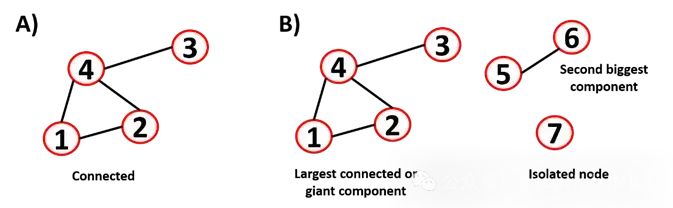
最大的隔离的节点子集被称为“孤岛”（island）。知道图是连通的还是不连通的是很重要的，有些算法很难处理不连通的图。

这可以在邻接矩阵中显示，其中不同的组件被写成对角线块(非零元素被限制在平方矩阵中)。我们称连接两个“孤岛”的链接“桥”（bridge）

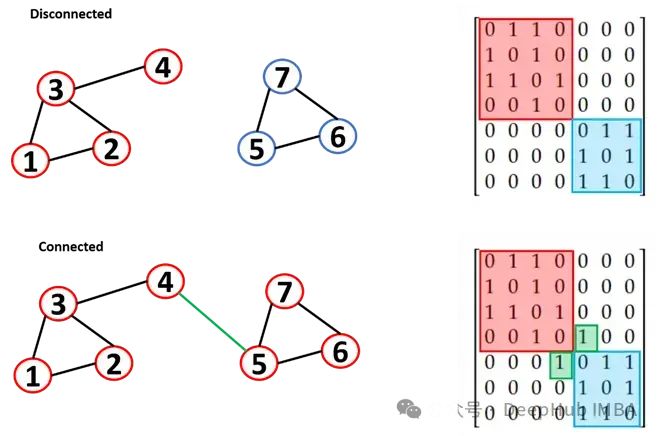
如果图很小，这种视觉检查很容易，但对于一个大图，检查连通性是非常有挑战的。

双部图

我们上面所看到的图称为单部图，其中只有一种类型的节点和一种类型的关系

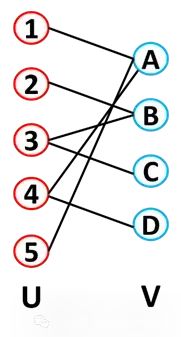
双部图是一种将节点划分为两个不相交集合（通常称为 U 和 V）的图。这些集合是独立的，U 集合中的每个节点都与 V 集合中的某个节点相连（每个链接只能连接一个集合中的节点到另一个集合中的节点）。因此，双部图是一种不存在 U-U 连接和 V-V 连接的图。有许多这样的例子：作者到论文（作者位于 U 集合，并且他们与他们撰写的论文即 V 集合相连）、演员（U）和他们参演的电影（V）、用户和产品、食谱和配料等。另一个例子是疾病网络，其中包括一组疾病和一组基因，只有包含已知会导致或影响该疾病的突变的基因才与该疾病相连。另一个例子是匹配，双部图可用于约会应用程序。对于一个有两组节点的双部图（U 有 m 个节点，V 有 n 个节点），可能的边的总数是 m*n，节点的总数是 m + n。

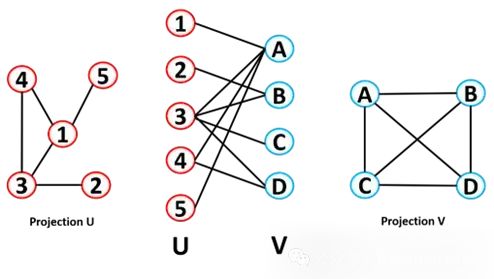
双部图可以折叠成两个单独的网络，U 的投影和 V 的投影。在 U 的投影中，如果两个节点连接到同一个 V 节点，则它们相连（V 投影的原理相同）。

如果需要，我们也可以构建一个三部图。总的来说，你可以拥有超过三种类型的节点，通常我们讲的是 k-部图。这种类型的图扩展了我们对双部图的看法。

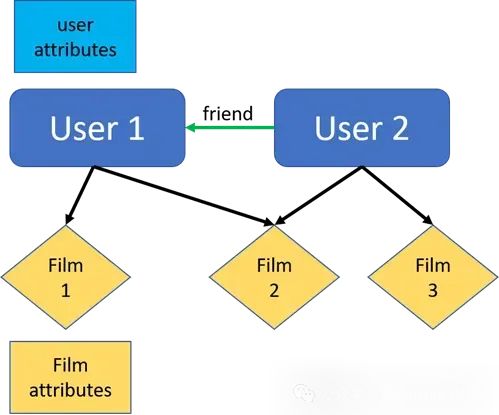
异构图

异构图（也称异质图）是一种具有不同类型的节点和边的图。

平面图

如果一幅图可以绘制成没有任何边相交的形式（对于图来说，如果可以以这种方式绘制，它被称为平面表示），则可以将其视为平面图。即使绘制时边相交，图也可以是平面的。看这个例子，这幅图可以重新绘制成平面表示。

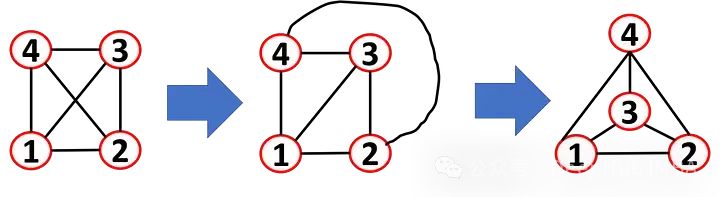
为什么知道我们是否可以有平面表示很有用？最常用的一个例子是绘制电路版，要保证电路不会相交。

循环图与非循环图

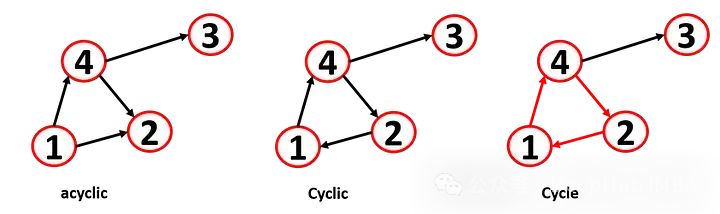
线路 (walk) 是节点的交替序列（u-v 的线路是从 u 开始并在 v 结束的节点序列）。路径（path）是序列中节点各不相同的线路（u-x-v 是一条路径，但 u-x-u-x-v 是线路但不是路径）。循环图是路径开始和结束于同一节点的图，因为不同的算法都有循环问题(所以有时需要通过切断一些连接将循环图转换为非循环图)。我们可以将前馈神经网络定义为有向无环图（DAG），因为DAG 总是有一个结束点（也称为叶子节点）。

总结

在本文中，我们介绍了什么是图及其主要属性，尽管图看起来很简单，但可以实现无限的变化。图是节点和边的集合;它没有顺序，没有开始也没有结束。我们可以通过它们定义不同类型的概念和数据。图还可以简洁地描述数据的许多属性，并为我们提供关于不同主题之间关系的信息。例如，我们可以为节点和边分配权重和属性。在以后的文章中，我们将讨论如何在这些网络中使用算法(以及如何表示它们)。

https://avoid.overfit.cn/post/ecbeccb28acf4271954d8c3ffe579d6a

作者：Salvatore Raieli