一、题目描述
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
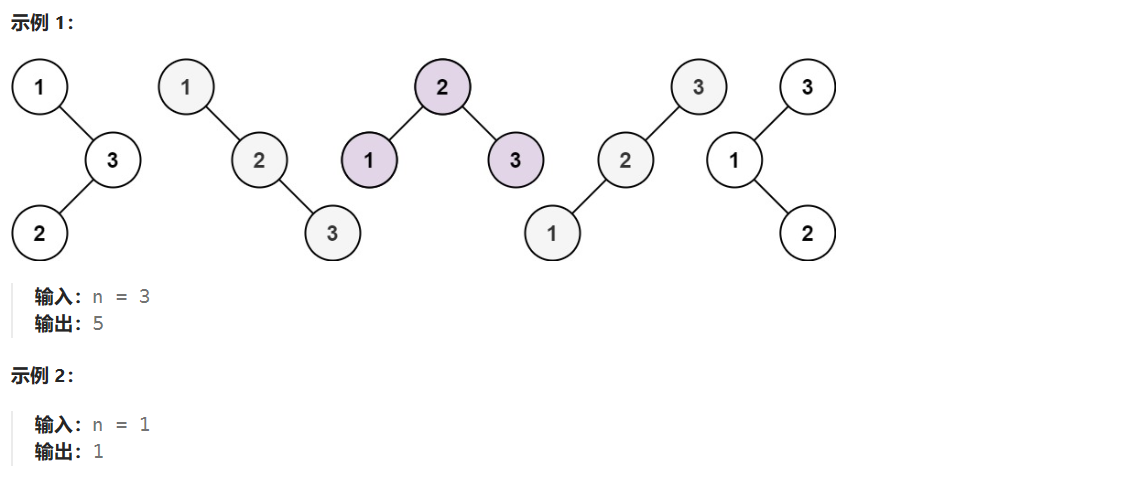
示例 1:

输入:head = [1,2,3,4,5], left = 2, right = 4 输出:[1,4,3,2,5]
示例 2:
输入:head = [5], left = 1, right = 1 输出:[5]
提示:
- 链表中节点数目为
n 1 <= n <= 500-500 <= Node.val <= 5001 <= left <= right <= n
二、解题思路
-
初始化: 创建一个哑结点
dummy,其next指针指向head。这样,即使head发生变化,我们也可以通过dummy.next获取到新的头结点。同时,我们还需要设置两个指针pre和cur,分别初始化为dummy。 -
定位: 将
pre移动到left - 1的位置,将cur移动到left的位置。 -
反转链表: 从
left到right,我们需要反转这部分链表。我们可以使用头插法进行链表的反转。具体来说,对于cur当前指向的节点,我们将其从链表中取出,然后将其插入到pre和pre.next之间。 -
返回结果: 反转完成后,返回
dummy.next即为新的头结点。
三、具体代码
class Solution {
public ListNode reverseBetween(ListNode head, int left, int right) {
ListNode dummy = new ListNode(0);
dummy.next = head;
ListNode pre = dummy;
// 定位到left的前一个节点
for (int i = 0; i < left - 1; i++) {
pre = pre.next;
}
// cur是left位置的节点
ListNode cur = pre.next;
// 反转left到right的链表
for (int i = 0; i < right - left; i++) {
ListNode temp = cur.next; // 取出下一个节点
cur.next = temp.next; // 断开连接
temp.next = pre.next; // 插入到pre和pre.next之间
pre.next = temp;
}
return dummy.next;
}
}
四、时间复杂度和空间复杂度
1. 时间复杂度
- 定位到
left的前一个节点的循环会运行left - 1次。 - 反转链表的循环会运行
right - left次。 - 因此,总的时间复杂度是
O(n),其中n是链表的长度。在最坏的情况下,left和right可能分别接近 1 和n,这将使得时间复杂度接近O(n)。
2. 空间复杂度
- 该算法只使用了几个额外的节点(
dummy,pre,cur,temp),不管链表有多长,这些额外的节点数量都是固定的。 - 因此,空间复杂度是
O(1),即常数空间复杂度。
综上所述,该算法的时间复杂度是 O(n),空间复杂度是 O(1)。
五、总结知识点
1. 链表操作:
- 链表节点的定义:使用
ListNode类来定义链表节点,每个节点包含一个val属性和一个next指针。 - 链表的遍历:通过节点的
next指针遍历链表。 - 链表的插入:在链表中插入一个新节点,需要修改相邻节点的
next指针。
2. 哑结点的使用:
- 哑结点(
dummy)是一个辅助节点,通常用于简化边界条件的处理。在这个问题中,它被用来确保即使在链表的头部进行操作,也能保持代码的一致性。
3. 指针的概念:
pre和cur是两个指针,用于跟踪链表中的当前位置。pre指向当前节点的前一个节点,而cur指向当前节点。
4. 链表的反转:
- 通过改变节点的
next指针方向,可以实现在原地反转链表的部分区间。这是通过将每个节点移动到链表的前端来完成的,这个过程通常称为头插法。
5. 循环的使用:
- 两个
for循环被用来定位到需要反转的链表部分,以及执行实际的反转操作。
6. 边界条件的处理:
- 代码中通过
left - 1和right - left来确定循环的次数,这样可以确保正确地定位到需要反转的链表区间,并且反转正确的节点数量。
7. 函数返回值:
- 函数返回
dummy.next,这是因为dummy是一个哑结点,它的next指针指向链表的真正头部。
以上就是解决这个问题的详细步骤,希望能够为各位提供启发和帮助。