自然对数函数的底数 e(也称为自然常数或欧拉数)与 π 一样,是数学中最伟大的常数之一。它大约为 2.718281828,是一个无理数,意味着它的小数部分无限且不重复。
与 π 和 √2 这些由几何发现而来的常数不同,e 是关于增长率和变化率的常数。它在描述人口增长、经济发展以及其他类型的增长过程中扮演着重要角色。为了理解 e 与增长率的关系,我们需要回溯到 17 世纪,探索最初它是怎样被发现的。
e 的由来

1683 年,瑞士数学家雅各布·伯努利(Jakob Bernoulli)在研究复利问题时发现了一个有趣的现象。
假设你把 1 块钱存到银行,有两种计息方案可供选择:
-
年利率为 100%,则一年后结算。
-
每半年结算一次利息,而半年利率为 50%。
对于第一种投资方法:
对于第二种投资方法:
对于第二种投资方案,一年后你将得到 块钱,看起来收益更高。
伯努利进一步思考,如果利息结算周期更短,比如每个月结算一次,年利率为 ,那么收益如何呢?
伯努利发现,随着结算频率的增加——按周计息、天、小时(如下图所示),最终收益还会逐渐增加,并趋向于一个特定的极限值。

当结算周期无限缩短,即 趋于无穷大时,复利收益趋近于一个极限值,这个现象可以用下面的数学公式来描述:
在这个表达式中, 代表计息周期的次数,而 就是每个计息周期的利率。
雅各布·伯努利意识到,这个极限值应该不仅与金融问题有关,实际上是一个普遍的数学常数,与许多自然增长和衰减过程有关。
虽然伯努利知道这个极限值介于 2 和 3 之间,他没有精确计算出这个数值,但他的工作引起了其他数学家的兴趣,包括莱昂哈德·欧拉(Leonhard Euler)。
解开 e 的神秘面纱
欧拉不仅计算出了 e 的值,并且还证明了 e 是无理数。他通过无穷级数和连分数的形式来研究 e,并计算出小数点后 18 位:
e 连分数形式如下图所示:
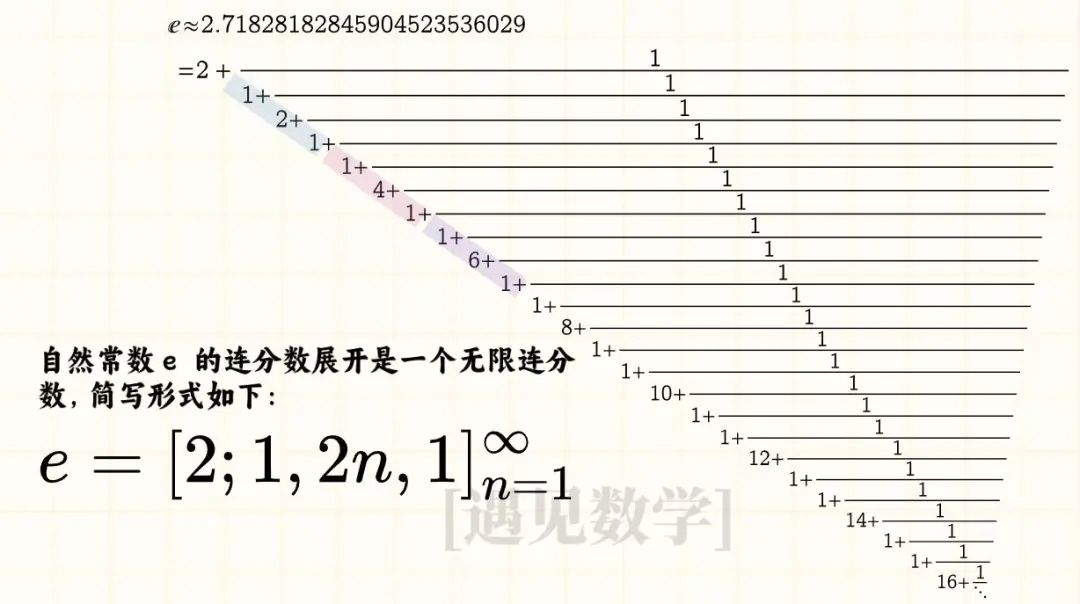
在 e 这个连分数中,模式是明显的:先是个位的 2,然后是交替的 1 和一直增加的偶数,每次出现都增加 2。于是,这个模式变成了 2, 1, 2, 1, 1, 4, 1, 1, 6, ...。这种模式是一个明显的规律,它持续无限地重复 —— 这个事实揭示了 的无理性。
当我们说一个数的连分数展开是无限的,实际上是在说这个数不能用有理数(即两个整数之比)来表示。因为有理数的连分数展开总是有限的或者最终会成为一个循环连分数。因此,连分数的无限性质意味着 是无理数,它的小数部分无穷无尽切不会重复。
e 的性质
e 是描述连续增长过程中的数学常数,这种增长模式在自然界和经济学中非常常见。
函数 是唯一一个导数是其自身的函数,在其图形上每一点处的斜率等于其函数值。特别是当 时,函数值、斜率都等于 e。这一性质使得 e 在微积分中非常重要,因为微积分正是研究变化率和极限的数学分支。每当在涉及增长率和变化率的微分方程中遇到涉及 e 的计算时,通常会更加简单处理。
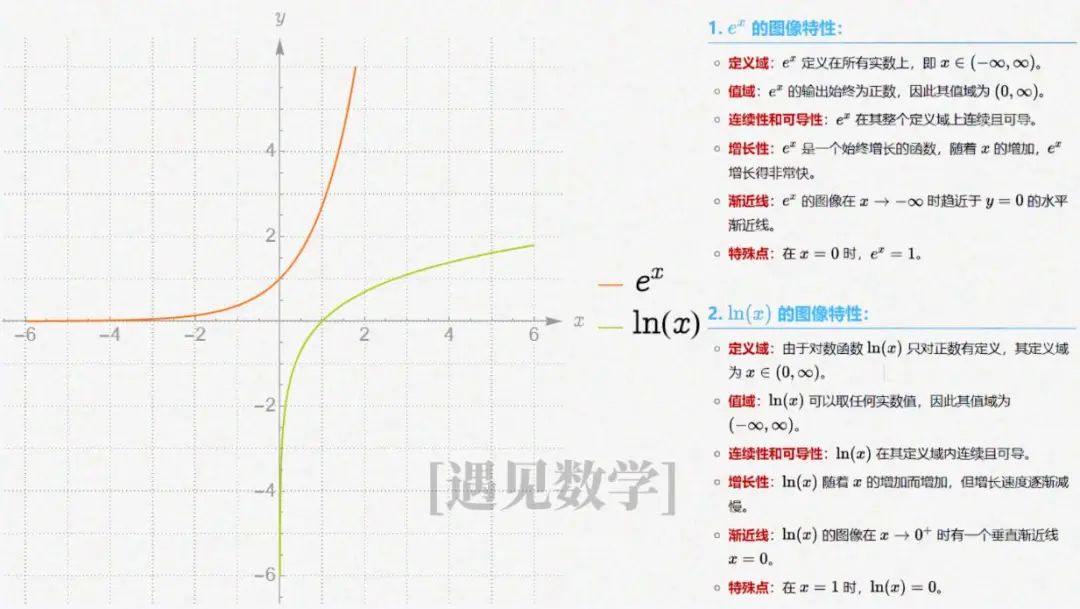
自然对数函数 和指数函数 是互为反函数,这意味着它们在 这条线上是对称的。
e 与 π 的联系
提到 e,我们通常会想到一个将5个著名常数汇集于一体的方程——欧拉恒等式(Euler's identity):
这个方程涵盖了 e、π、i、1、0 这些数学中最重要的常数,凝聚了复数、指数函数、圆周率及相等关系的基本概念,被很多人视为数学中最美公式。
欧拉恒等式其实是欧拉公式 时特殊形式,欧拉公式是通过复数指数函数连接 和 的一个著名公式,它说明了任何实数 都满足:
和 之间的另一个联系是高斯积分:
这个积分在概率论和统计学中非常重要,尤其是在正态分布的背景下。
另外在残差定理中, 的指数形式是计算围绕极点的闭合路径积分的关键,而在傅里叶变换中, 和 体现了信号的时频转换和周期性特征。