严格讲指数加权平均数并不是机器学习中的专有知识,但他是诸多梯度下降优化算法的基础,所有我打算专门写一篇文章来介绍这种计算平均数的方法。还是老规矩,首先给大家来两个例子感受一下什么是指数加权平均数。
一、两个例子感性理解什么是指数加权平均数
(1)记录体重平均值
假设你每天都在记录你的体重,想要了解一段时间内的体重变化趋势。传统的平均方法会把所有天数的体重加起来再除以天数,得到一个“平均水平”。但这种方法忽略了最近体重变化的重要性。
指数加权平均就像是给你的体重记录本添上了一个“记忆偏好”。它更看重最近的数据,对过去的数据给予逐渐减小的重视。就像是你在回顾体重记录时,对于昨天的体重记得很清楚,上周的体重记忆就开始模糊了,而一个月前的体重就只留下个大概印象。
(2)拍照动态模糊
假设你拿着一个相机在拍摄一段长时间的动态场景,如果你希望既能捕捉到最近发生的动作,又不完全丢弃过去的画面,你可能会选择使用一个“动态模糊”效果。在这个效果下,最近的画面是清晰的,而过去的且渐趋远去的画面则越来越模糊。
二、指数加权平均数的定义
指数加权平均数(Exponential Weighted Moving Average,EWMA)在数学上是这样定义的。设为在时间点
的指数加权平均数,而
为在时间点
的实际值。EWMA通过以下递归公式计算得出:
在这个公式中:
| 符号 | 描述 |
| 一个介于 0 和 1 之间的权重衰减因子(也称为平滑因子),它决定了过去观测值的影响程度。 | |
| 前一时刻的EWMA值。 | |
| 当前时刻 | |
当前时刻 |
这种计算方式特别适用于处理时序数据,用于平滑短期波动,并能够更快地捕捉到长期趋势的变化。在时间序列分析、金融市场分析和深度学习中的某些优化算法,比如梯度下降的动量方法中,指数加权平均数被广泛使用。
三、实际拿个例子计算一下
某城市4月份30天气温数据如下表:
| 日期 | 最高温度(℃) | 最低温度(℃) | 天气状况 |
|---|---|---|---|
| 4月1日 | 18 | 8 | 晴 |
| 4月2日 | 20 | 9 | 多云 |
| 4月3日 | 16 | 6 | 小雨 |
| 4月4日 | 14 | 5 | 阴 |
| 4月5日 | 17 | 7 | 晴 |
| 4月6日 | 22 | 10 | 晴 |
| 4月7日 | 21 | 9 | 多云 |
| 4月8日 | 19 | 5 | 晴转多云 |
| 4月9日 | 12 | 3 | 阴 |
| 4月10日 | 23 | 10 | 晴 |
| 4月11日 | 15 | 6 | 小雨 |
| 4月12日 | 16 | 7 | 阴 |
| 4月13日 | 19 | 8 | 晴 |
| 4月14日 | 21 | 11 | 多云 |
| 4月15日 | 18 | 5 | 晴 |
| 4月16日 | 14 | 3 | 阴转小雨 |
| 4月17日 | 17 | 6 | 晴 |
| 4月18日 | 20 | 9 | 晴 |
| 4月19日 | 13 | 4 | 阴 |
| 4月20日 | 19 | 8 | 多云 |
| 4月21日 | 22 | 10 | 晴 |
| 4月22日 | 16 | 5 | 阴 |
| 4月23日 | 15 | 7 | 小雨 |
| 4月24日 | 18 | 6 | 晴 |
| 4月25日 | 20 | 9 | 晴 |
| 4月26日 | 13 | 4 | 阴 |
| 4月27日 | 19 | 8 | 多云 |
| 4月28日 | 21 | 11 | 晴 |
| 4月29日 | 16 | 5 | 阴 |
| 4月30日 | 17 | 7 | 小雨转晴 |
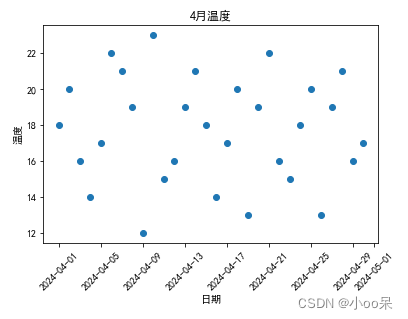
画出30天最高温度的散点图,X轴是日期,Y轴是最高温度:
第1天:
- 最高温度:18℃
- 由于是第一天,我们将
设为当天的实际最高温度:
第2天:
- 最高温度:20℃
- 使用EWMA计算公式,以
作为前一日的EWMA值,和
作为最高温度:
第3天:
- 最高温度:16℃
- 类似地,我们使用
作为前一日的EWMA值,和
作为最高温度: