文章目录
- 0. 概述
- 1. 操作与接口
- 2. 操作实例
- 3. 实现
- 4. 栈与递归
- 5. 应用
- 5.1 逆序输出
- 5.1.1 进制转换
- 5.1.1.1 思路
- 5.1.1.2 算法实现
- 5.2 递归嵌套
- 5.2.1 栈混洗
- 5.2.1.1 混洗
- 5.2.1.2 计数
- 5.2.1.3 甄别
- 5.2.2 括号匹配
- 5.2.2.1 构思
- 5.2.2.2 实现
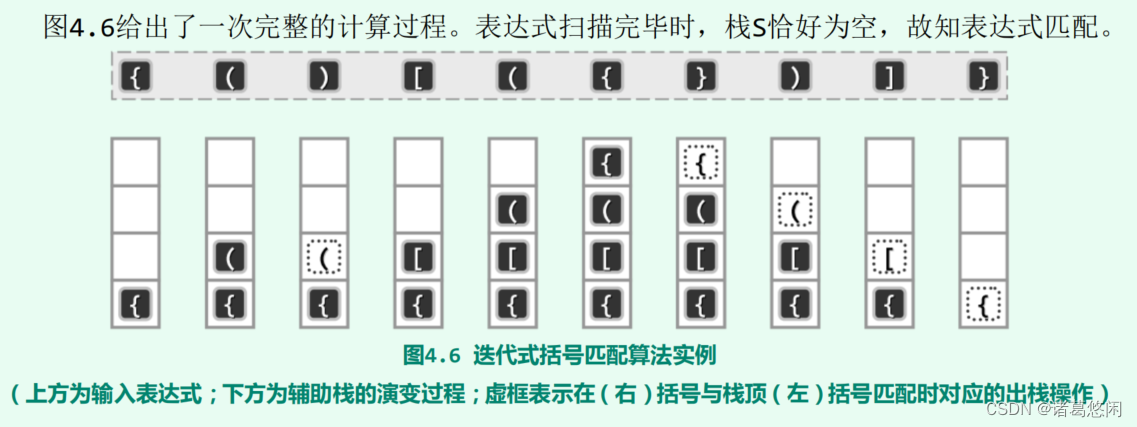
- 5.2.2.3 实例
- 5.3 延迟缓冲
- 5.3.1 中缀表达式
- 5.3.1.1 表达式求值
- 5.3.1.2 优先级表
- 5.3.1.3 求值算法
- 5.3.2 逆波兰表达式(后缀表达式)
- 5.3.2.1 RPN
- 5.3.2.2 RPN实例
- 5.3.2.3 infix 到postfix 转换
0. 概述
介绍下栈的接口与应用。
1. 操作与接口
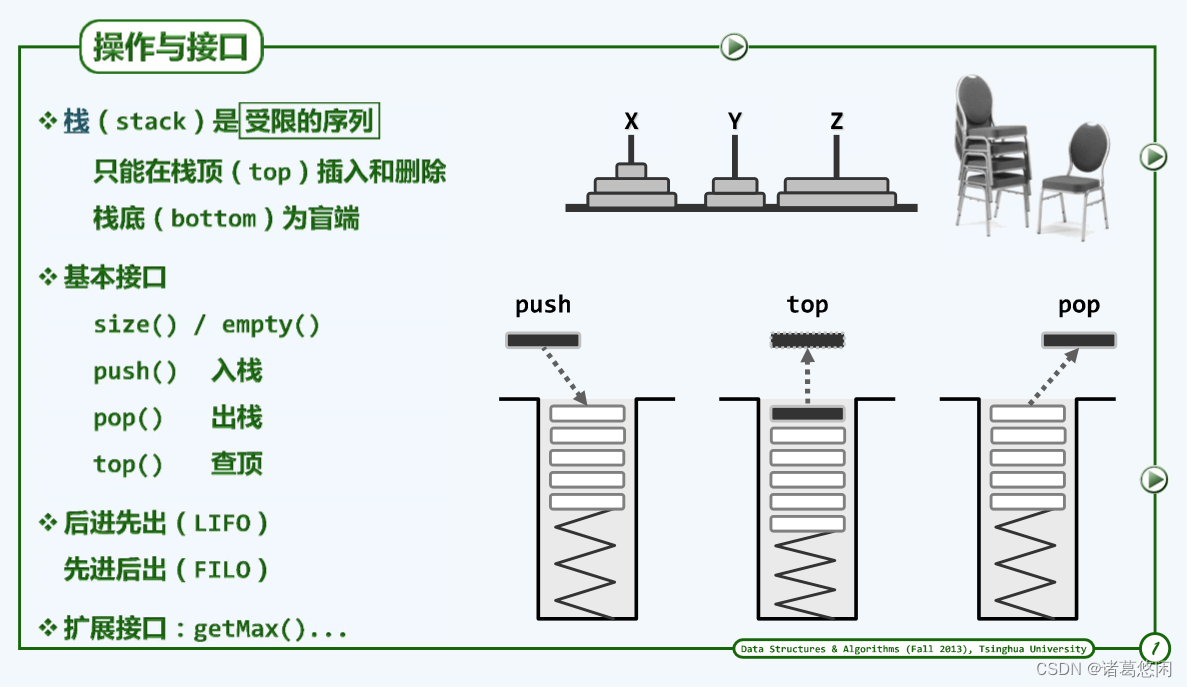
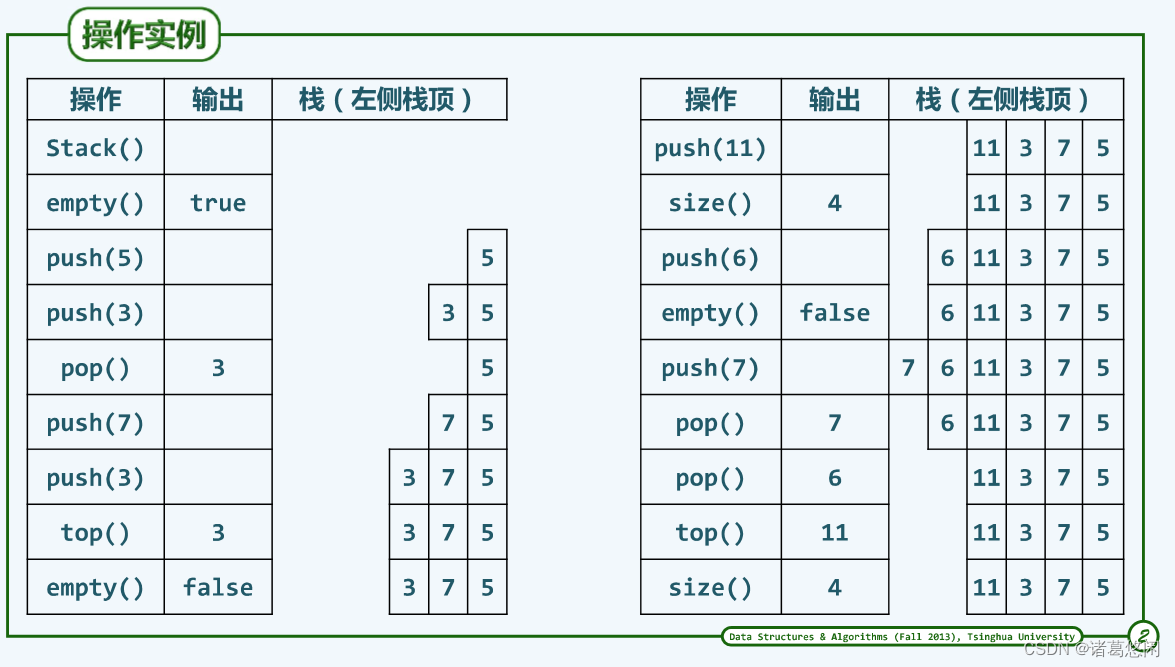
2. 操作实例
3. 实现

基于向量
#include "Vector/Vector.h" //以向量为基类,派生出栈模板类
template <typename T>
class Stack: public Vector<T> { //将向量的首/末端作为栈底/顶
public: //原有接口一概沿用
void push ( T const& e ) { insert ( e ); } //入栈:等效于将新元素作为向量的末元素插入
T pop() { return remove ( size() - 1 ); } //出栈:等效于删除向量的末元素
T& top() { return ( *this ) [size() - 1]; } //取顶:直接返回向量的末元素
};
基于列表
#include "List/List.h" //以列表为基类,派生出栈模板类
template <typename T>
class Stack: public List<T> { //将列表的首/末端作为栈底/顶
public: //原有接口一概沿用
void push ( T const& e ) { insertAsLast ( e ); } //入栈:等效于将新元素作为列表的末元素插入
T pop() { return remove ( last() ); } //出栈:等效于删除列表的末元素
T& top() { return last()->data; } //取顶:直接返回列表的末元素
};
4. 栈与递归

5. 应用
典型应用场合

5.1 逆序输出
5.1.1 进制转换
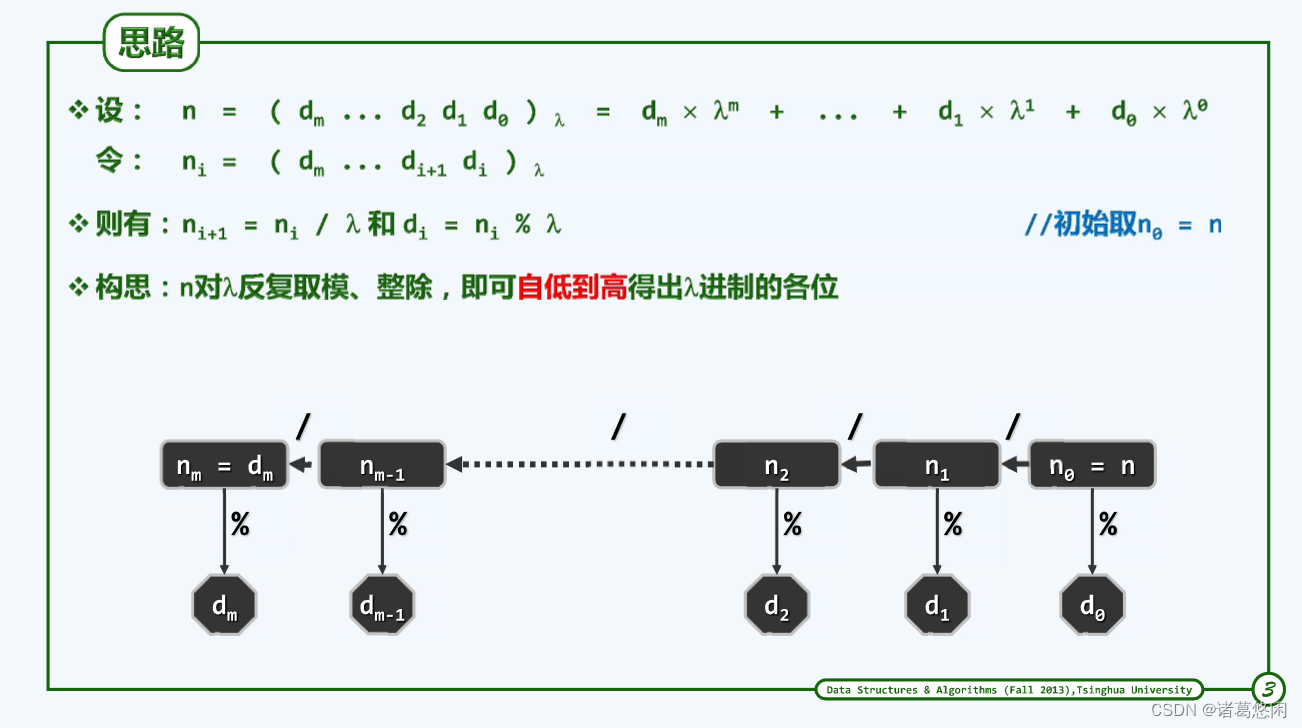
5.1.1.1 思路
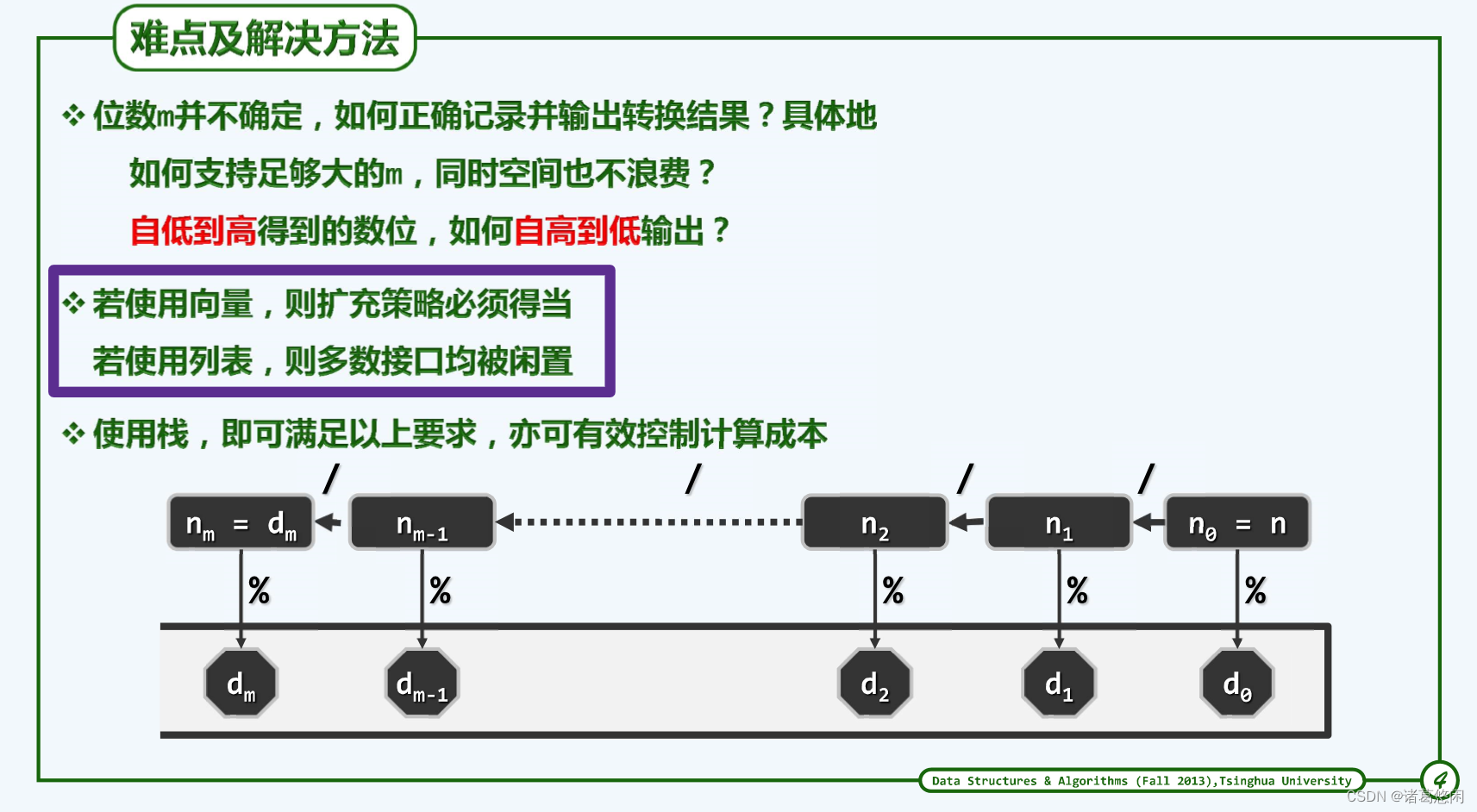
5.1.1.2 算法实现
- 递归实现
void convert ( Stack<char>& S, __int64 n, int base ) { //十进制数n到base进制的转换(递归版)
static char digit[] //0 < n, 1 < base <= 16,新进制下的数位符号,可视base取值范围适当扩充
= { '0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F' };
if ( 0 < n ) { //在尚有余数之前,不断
convert ( S, n / base, base ); //通过递归得到所有更高位
S.push ( digit[n % base] ); //输出低位
}
} //新进制下由高到低的各数位,自顶而下保存于栈S中
- 迭代实现
优化点:
这里的静态数位符号表在全局只需保留一份,但与一般的递归函数一样,该函数在递归调用栈中的每一帧都仍需记录参数S、n和base。将它们改为全局变量固然可以节省这部分空间,但依然不能彻底地避免因调用栈操作而导致的空间和时间消耗。
改写成迭代版将空间消耗降至O(1)。
void convert ( Stack<char>& S, __int64 n, int base ) { //十进制数n到base进制的转换(迭代版)
static char digit[] //0 < n, 1 < base <= 16,新进制下的数位符号,可视base取值范围适当扩充
= { '0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F' };
while ( n > 0 ) { //由低到高,逐一计算出新进制下的各数位
int remainder = ( int ) ( n % base ); S.push ( digit[remainder] ); //余数(当前位)入栈
n /= base; //n更新为其对base的除商
}
} //新进制下由高到低的各数位,自顶而下保存于栈S中
5.2 递归嵌套
5.2.1 栈混洗
5.2.1.1 混洗
栈混洗就是按照某种约定的规则对栈中元素进行重新的排列。
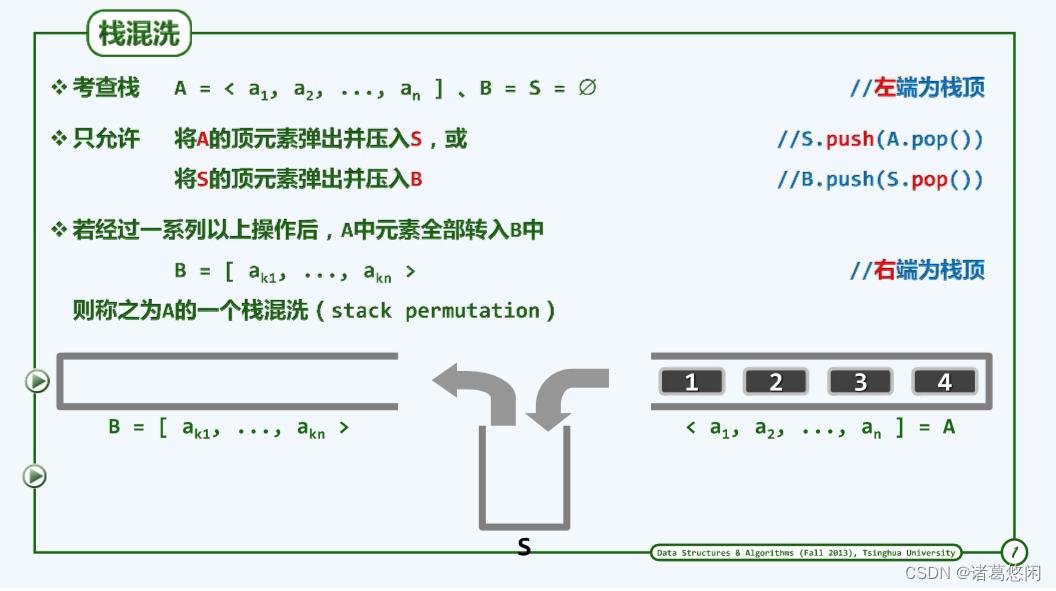
上图采用约定尖括号<表示栈顶,方括号]表示栈底。
在遵守以上规则的前提下,同一输入序列完全可以导出不同的栈混洗序列。
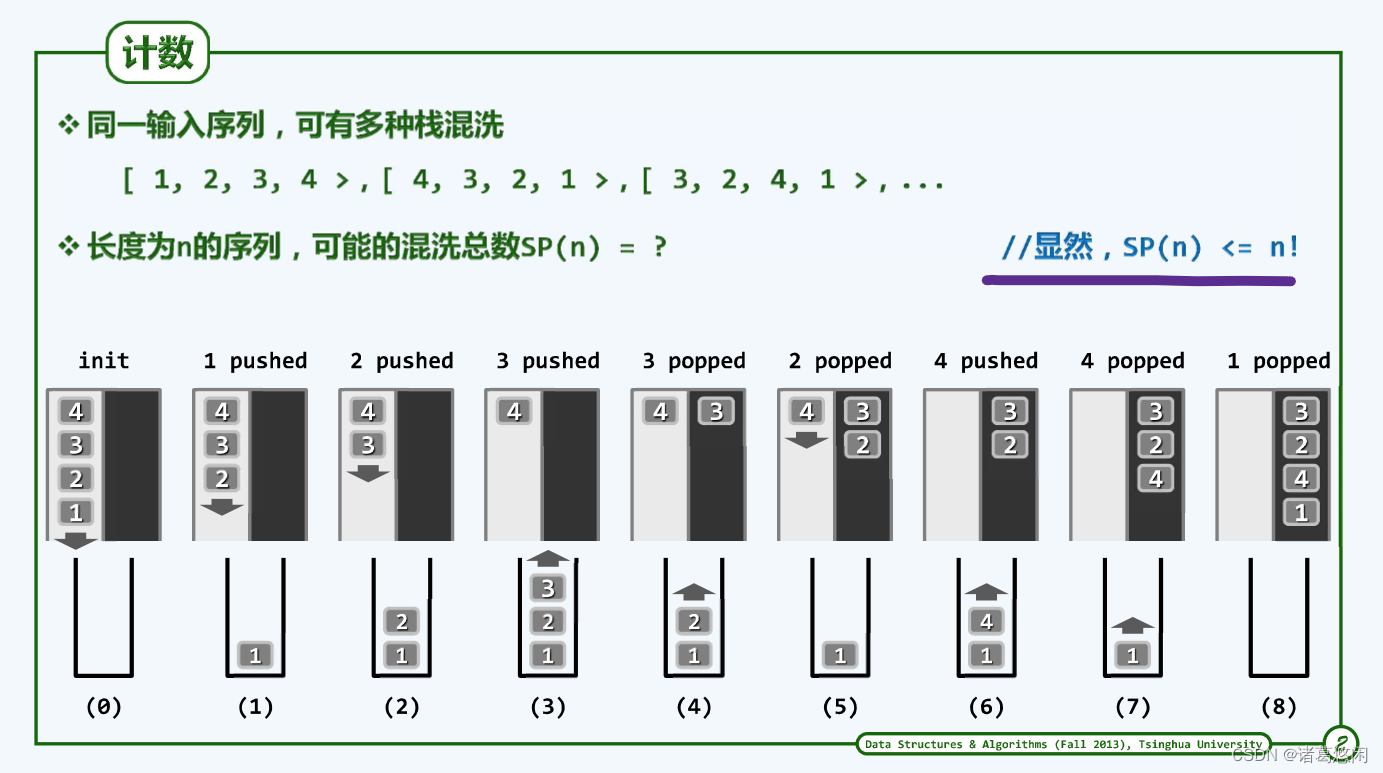
n个元素的栈混洗总数不会超过全排列n!。
一般地对于长度为n的输入序列,每一栈混洗都对应于由栈S的n次push和n次pop构成的某一合法操作序列比如[ 3, 2,4, 1>
即对应于操作序列:
{push, push, push, pop, pop, push, pop, pop }
反之,由n次push和n次pop构成的任何操作序列,只要满足“任一前缀中的push不少于pop”这一限制,则该序列也必然对应于
某个栈混洗。
5.2.1.2 计数
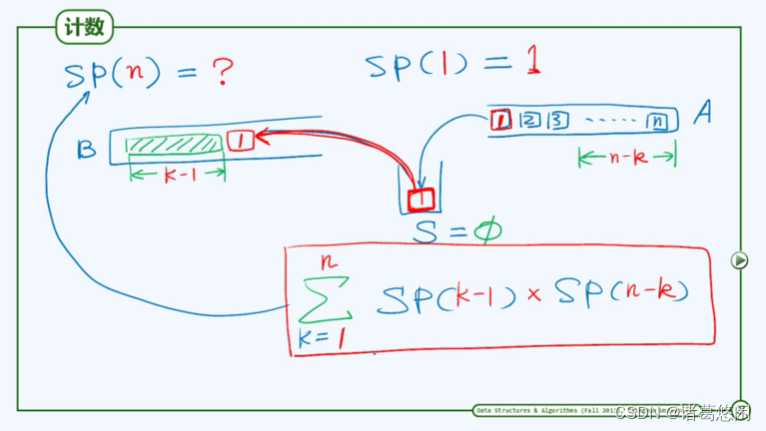
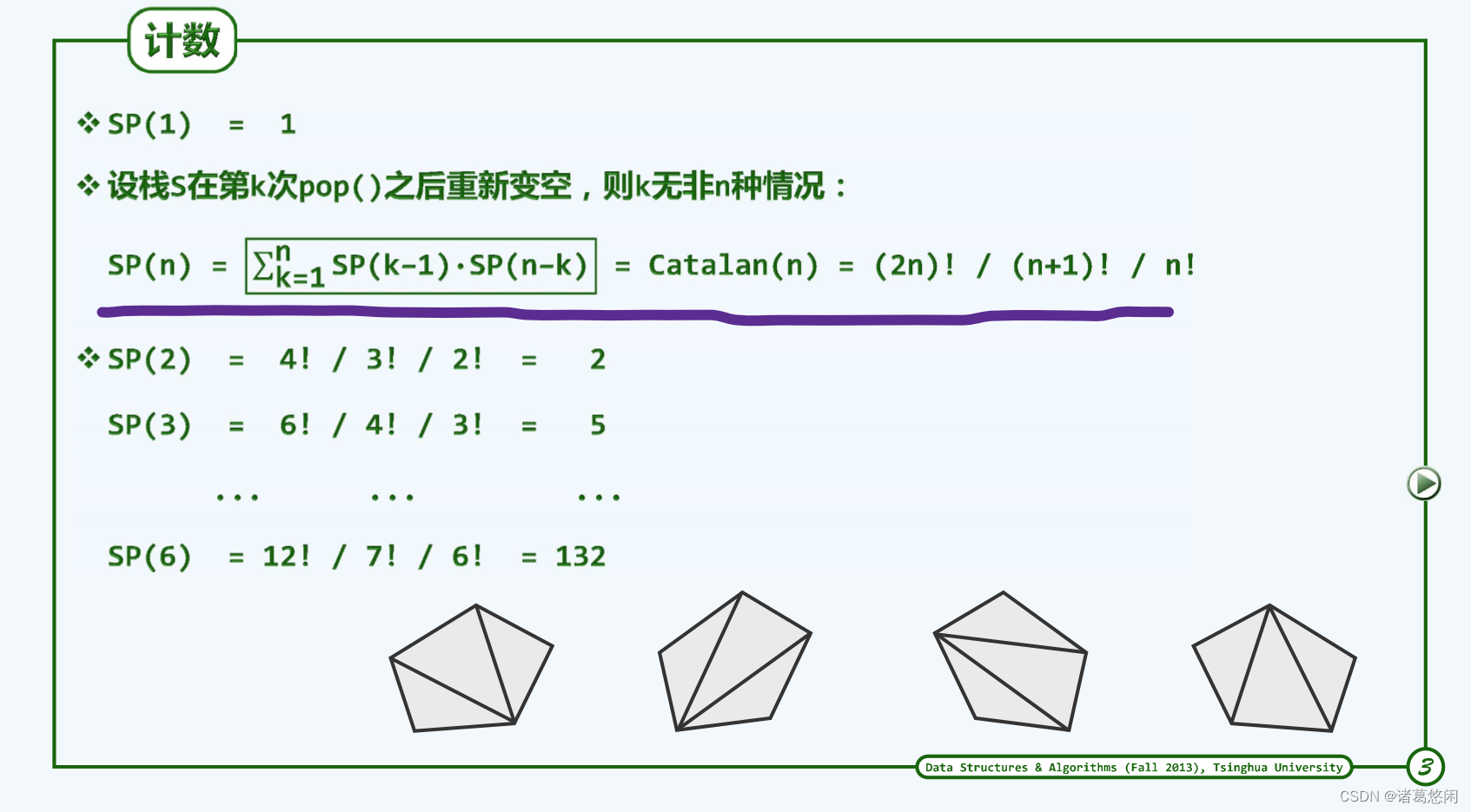
假定输入栈A中共有n个元素,自顶向下依次编号为1,2,3 … n。将注意力放在第一个元素1上,它将被首次推入中转栈S中,若1号元素被弹出,则栈S就是空栈,此时在栈B中包括刚推入的1号元素,累计共有k个元素。那么栈A中就应该还留存有最后的n-k个元素。此时B中k个元素和A中n-k个元素它们的栈混洗是相互独立的,故1号元素作为第k个元素被推入B中的情况,累计栈混洗总数如下
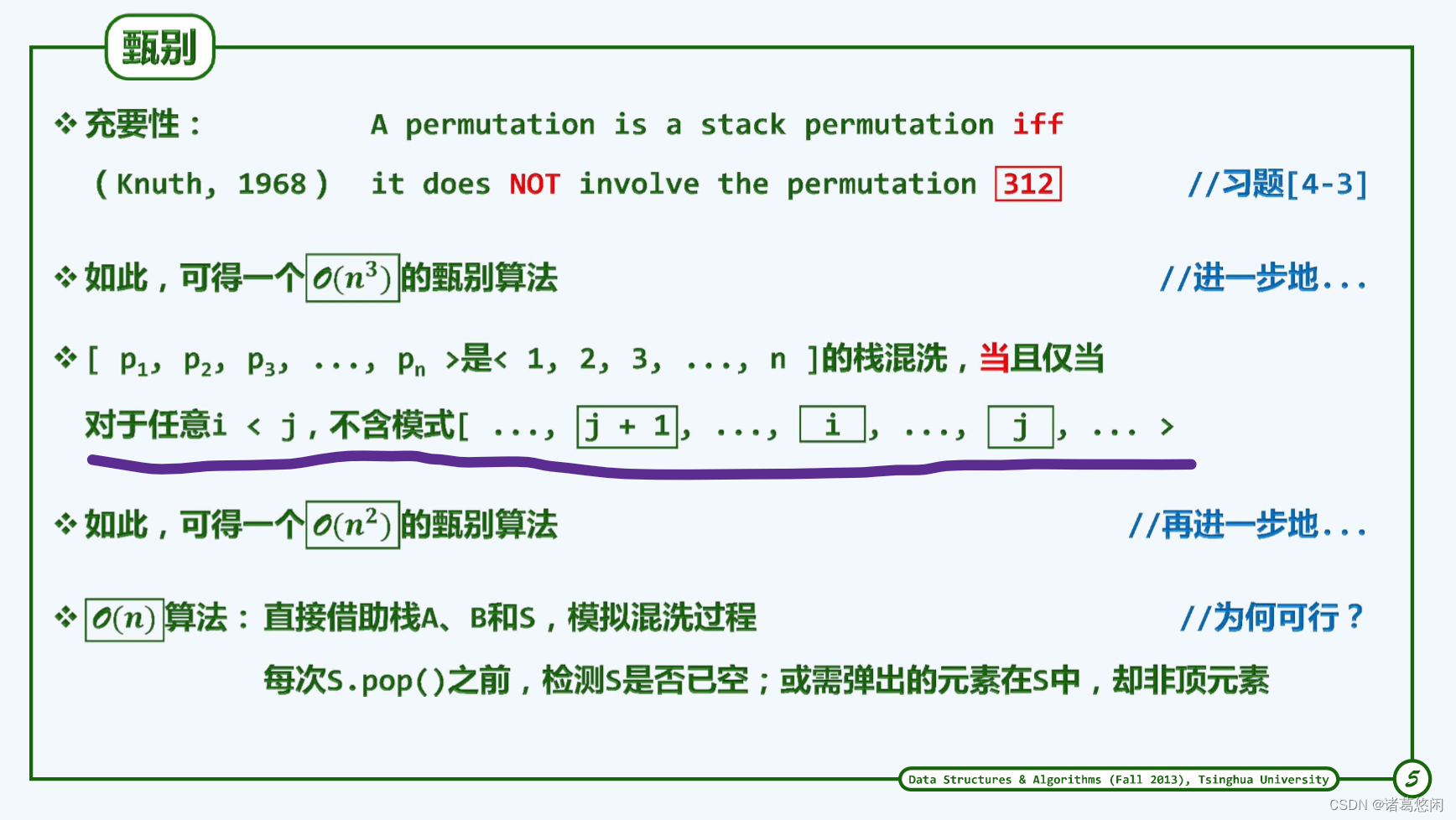
5.2.1.3 甄别

5.2.2 括号匹配
5.2.2.1 构思

5.2.2.2 实现
算法思想:只要将push、pop操作分别与左、右括号相对应,则长度为n的栈混洗,必然与由n对括号组成的合法表达式彼此对应。 比如,栈混洗[ 3, 2, 4, 1 >对应于表达式"( ( ( ) ) ( ) )"。按照这一理解,借助栈结构,只需扫描一趟表达式,即可在线性时间内,判定其中的括号是否匹配。
bool paren ( const char exp[], int lo, int hi ) { //表达式括号匹配检查,可兼顾三种括号
Stack<char> S; //使用栈记录已发现但尚未匹配的左括号
for ( int i = lo; i <= hi; i++ ) /* 逐一检查当前字符 */
switch ( exp[i] ) { //左括号直接进栈;右括号若与栈顶失配,则表达式必不匹配
case '(': case '[': case '{': S.push ( exp[i] ); break;
case ')': if ( ( S.empty() ) || ( '(' != S.pop() ) ) return false; break;
case ']': if ( ( S.empty() ) || ( '[' != S.pop() ) ) return false; break;
case '}': if ( ( S.empty() ) || ( '{' != S.pop() ) ) return false; break;
default: break; //非括号字符一律忽略
}
return S.empty(); //整个表达式扫描过后,栈中若仍残留(左)括号,则不匹配;否则(栈空)匹配
}
5.2.2.3 实例
5.3 延迟缓冲
在一些应用问题中,输入可分解为多个单元并通过迭代依次扫描处理,但过程中的各步计算往往滞后于扫描的进度,需要待到必要的信息已完整到一定程度之后,才能作出判断并实施计算。在这类场合,栈结构则可以扮演数据缓冲区的角色。
中缀表达式算法的求解过程同逆波兰表达式算法,下面介绍下。
5.3.1 中缀表达式
5.3.1.1 表达式求值
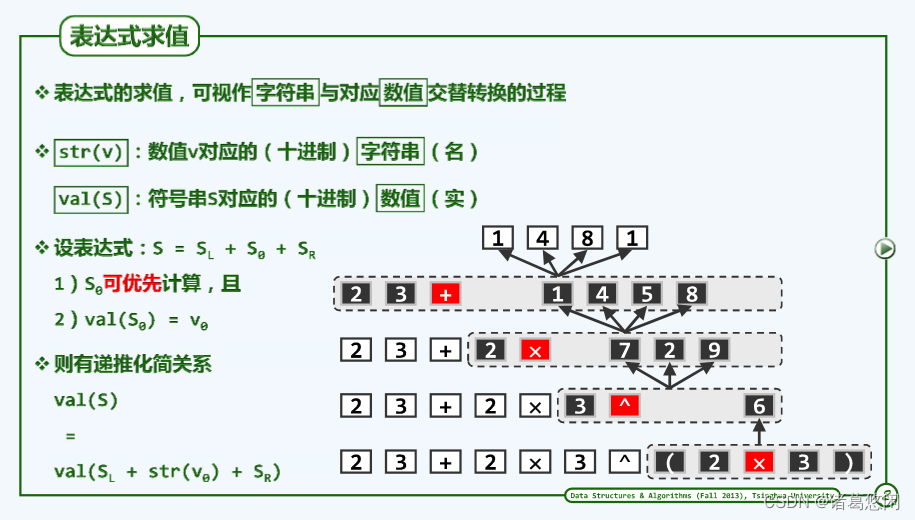


5.3.1.2 优先级表
将不同运算符之间的运算优先级关系,描述为一张二维表格。

#define N_OPTR 9 //运算符总数
typedef enum { ADD, SUB, MUL, DIV, POW, FAC, L_P, R_P, EOE } Operator; //运算符集合
//加、减、乘、除、乘方、阶乘、左括号、右括号、起始符与终止符
const char pri[N_OPTR][N_OPTR] = { //运算符优先等级 [栈顶] [当前]
/* |-------------------- 当 前 运 算 符 --------------------| */
/* + - * / ^ ! ( ) \0 */
/* -- + */ '>', '>', '<', '<', '<', '<', '<', '>', '>',
/* | - */ '>', '>', '<', '<', '<', '<', '<', '>', '>',
/* 栈 * */ '>', '>', '>', '>', '<', '<', '<', '>', '>',
/* 顶 / */ '>', '>', '>', '>', '<', '<', '<', '>', '>',
/* 运 ^ */ '>', '>', '>', '>', '>', '<', '<', '>', '>',
/* 算 ! */ '>', '>', '>', '>', '>', '>', ' ', '>', '>',
/* 符 ( */ '<', '<', '<', '<', '<', '<', '<', '=', ' ',
/* | ) */ ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ',
/* -- \0 */ '<', '<', '<', '<', '<', '<', '<', ' ', '='
};
5.3.1.3 求值算法
double evaluate ( char* S, char* RPN ) { //对(已剔除白空格的)表达式S求值,并转换为逆波兰式RPN
Stack<double> opnd; Stack<char> optr; //运算数栈、运算符栈 /*DSA*/任何时刻,其中每对相邻元素之间均大小一致
/*DSA*/ char* expr = S;
optr.push ( '\0' ); //尾哨兵'\0'也作为头哨兵首先入栈
while ( !optr.empty() ) { //在运算符栈非空之前,逐个处理表达式中各字符
if ( isdigit ( *S ) ) { //若当前字符为操作数,则
readNumber ( S, opnd ); append ( RPN, opnd.top() ); //读入操作数,并将其接至RPN末尾
} else //若当前字符为运算符,则
switch ( priority ( optr.top(), *S ) ) { //视其与栈顶运算符之间优先级高低分别处理
case '<': //栈顶运算符优先级更低时
optr.push ( *S ); S++; //计算推迟,当前运算符进栈
break;
case '=': //优先级相等(当前运算符为右括号或者尾部哨兵'\0')时
optr.pop(); S++; //脱括号并接收下一个字符
break;
case '>': { //栈顶运算符优先级更高时,可实施相应的计算,并将结果重新入栈
char op = optr.pop(); append ( RPN, op ); //栈顶运算符出栈并续接至RPN末尾
if ( '!' == op ) //若属于一元运算符
opnd.push ( calcu ( op, opnd.pop() ) ); //则取一个操作数,计算结果入栈
else { //对于其它(二元)运算符
double opnd2 = opnd.pop(), opnd1 = opnd.pop(); //取出后、前操作数 /*DSA*/提问:可否省去两个临时变量?
opnd.push ( calcu ( opnd1, op, opnd2 ) ); //实施二元计算,结果入栈
}
break;
}
default : exit ( -1 ); //逢语法错误,不做处理直接退出
}//switch
/*DSA*/displayProgress ( expr, S, opnd, optr, RPN );
}//while
return opnd.pop(); //弹出并返回最后的计算结果
}
算法思想:
~~~~~~~
该算法自左向右扫描表达式,并对其中字符逐一做相应的处理。那些已经扫描过但(因信息不足)尚不能处理的操作数与运算符,将分别缓冲至栈opnd和栈optr。一旦判定已缓存的子表达式优先级足够高,便弹出相关的操作数和运算符,随即执行运算,并将结果压入栈opnd。
~~~~~~~
请留意这里区分操作数和运算符的技巧。一旦当前字符由非数字转为数字,则意味着开始进入一个对应于操作数的子串范围。由于这里允许操作数含有多个数位,甚至可能是小数。
void readNumber ( char*& p, Stack<double>& stk ) { //将起始于p的子串解析为数值,并存入操作数栈
stk.push ( ( double ) ( *p - '0' ) ); //当前数位对应的数值进栈
while ( isdigit ( * ( ++p ) ) ) //若有后续数字(多位整数),则
stk.push ( stk.pop() * 10 + ( *p - '0' ) ); //追加之(可能上溢)
if ( '.' == *p ) { //若还有小数部分
double fraction = 1; //则
while ( isdigit ( * ( ++p ) ) ) //逐位
stk.push ( stk.pop() + ( *p - '0' ) * ( fraction /= 10 ) ); //加入(可能下溢)
}
}
根据当前字符及其后续的若干字符,利用另一个栈解析出当前的操作数。解析完毕,当前字符将再次聚焦于一个非数字字符。
不同优先级的处置如下:
调用priority ()函数,将其与栈optr的栈顶操作符做一比较之后,即可视二者的优先级高低,分三种情况相应地处置。
Operator optr2rank ( char op ) { //由运算符转译出编号
switch ( op ) {
case '+' : return ADD; //加
case '-' : return SUB; //减
case '*' : return MUL; //乘
case '/' : return DIV; //除
case '^' : return POW; //乘方
case '!' : return FAC; //阶乘
case '(' : return L_P; //左括号
case ')' : return R_P; //右括号
case '\0': return EOE; //起始符与终止符
default : exit ( -1 ); //未知运算符
}
}
char priority ( char op1, char op2 ) //比较两个运算符之间的优先级
{ return pri[optr2rank ( op1 ) ][optr2rank ( op2 ) ]; }
将其与栈optr的栈顶操作符做一比较之后,即可视二者的优先级高低,分三种情况相应地处置。
1)若当前运算符的优先级更高,则optr中的栈顶运算符尚不能执行
2)反之,一旦栈顶运算符的优先级更高,则可以立即弹出并执行对应的运算
一目运算符!弹出一个数,双目运算符弹出两个数。
3)当前运算符与栈顶运算符的优先级“相等”
对右括号的上述处理方式,将在optr栈顶出现操作符'('时终止。除左、
右括号外,还有一种优先级相等的合法情况,即pri['\0']['\0'] = '='。
5.3.2 逆波兰表达式(后缀表达式)
5.3.2.1 RPN


5.3.2.2 RPN实例
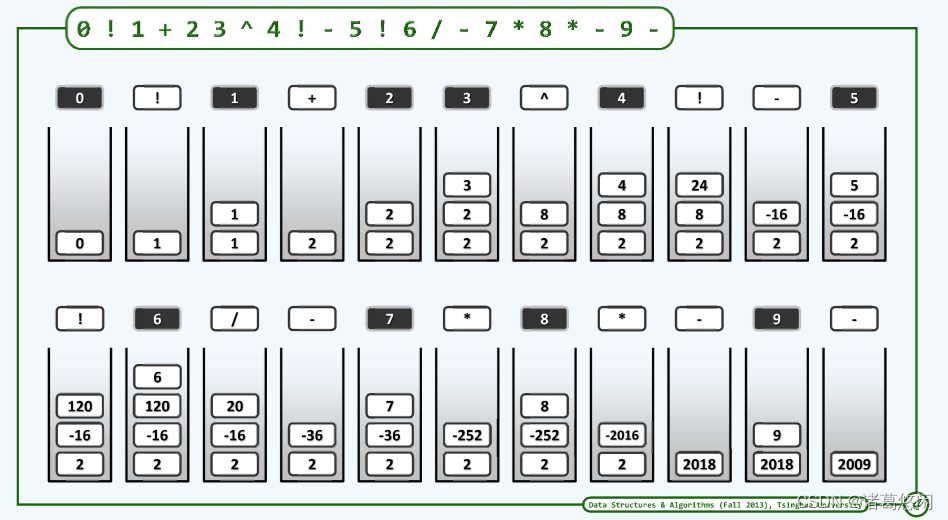
5.3.2.3 infix 到postfix 转换


上述evaluate()算法在对表达式求值的同时,也顺便完成了从常规表达式到RPN表达式的转换。
该算法借助append()函数将各操作数和运算符适时地追加至串rpn的末尾,直至得到完整的RPN表达式。
void append ( char* rpn, double opnd ) { //将操作数接至RPN末尾
char buf[64];
if ( ( int ) opnd < opnd ) sprintf ( buf, "%6.2f \0", opnd ); //浮点格式,或
else sprintf ( buf, "%d \0", ( int ) opnd ); //整数格式
strcat ( rpn, buf ); //RPN加长
}
void append ( char* rpn, char optr ) { //将运算符接至RPN末尾
int n = strlen ( rpn ); //RPN当前长度(以'\0'结尾,长度n + 1)
sprintf ( rpn + n, "%c \0", optr ); //接入指定的运算符
}
这里,在接入每一个新的操作数或操作符之前,都要调用realloc()函数以动态地扩充RPN表达式的容量,因此会在一定程度上影响时间效率。
在十分注重这方面性能的场合,读者可以做适当的改进——比如,有必要扩容时即令容量加倍。