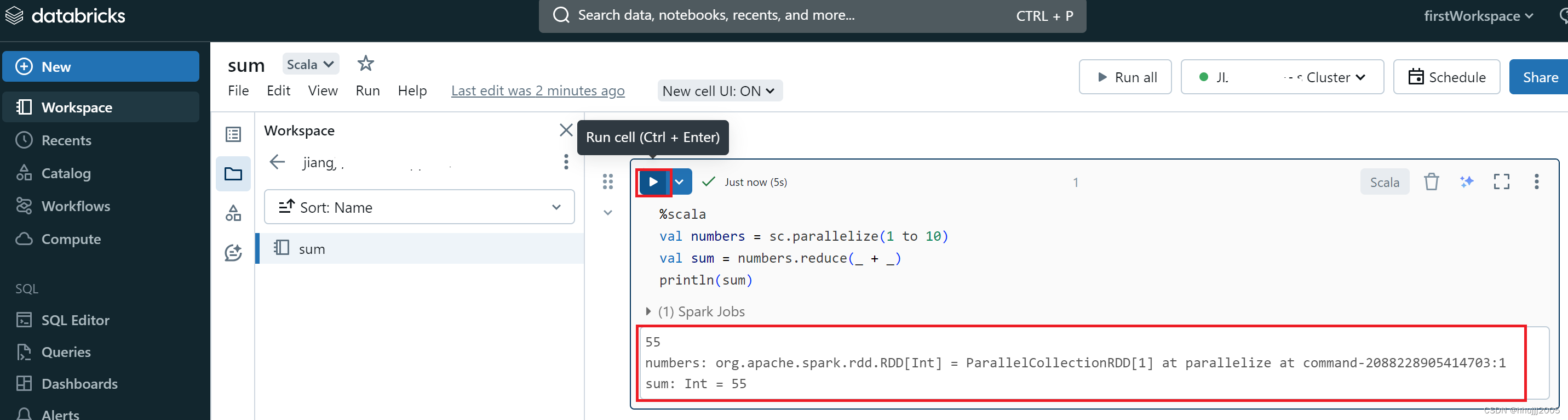
104. 二叉树的最大深度 - 力扣(LeetCode)

递归判断,当前节点的最大深度为1 + max(左节点的最大深度,右节点的最大深度)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int dfs(TreeNode *cur)
{
if (cur == nullptr) return 0;
return 1 + max(dfs(cur->left), dfs(cur->right));
}
int maxDepth(TreeNode* root) {
return dfs(root);
}
};
102. 二叉树的层序遍历 - 力扣(LeetCode)
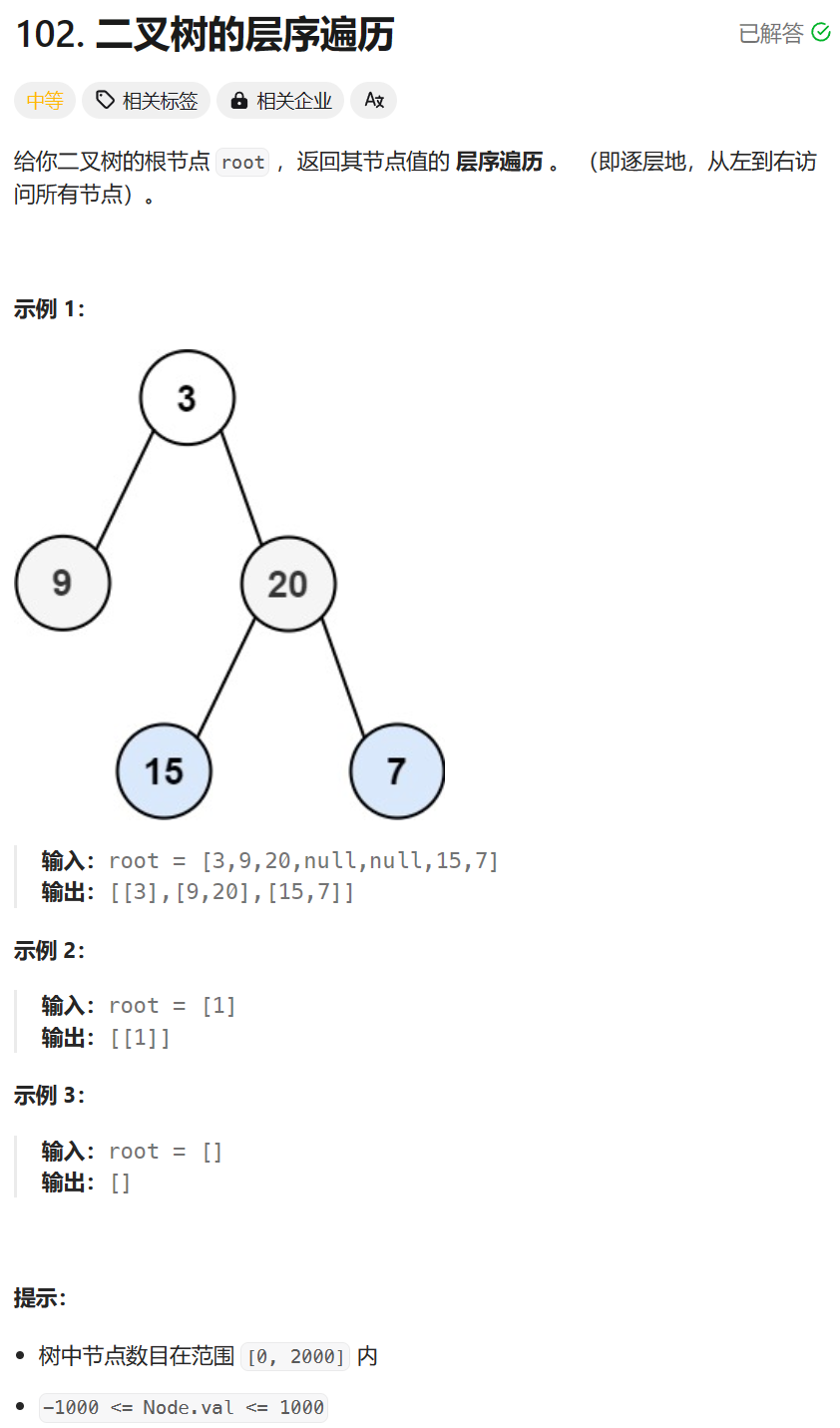
使用队列,每次出队前先记录当前队列的长度k,k为层的节点数量
此时只需要将前k个节点出队并将节点的左右子节点入队即可
在出队的同时维护答案
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ans;
if (root == nullptr) return ans;
queue<TreeNode*> q;
q.push(root);
while (q.size())
{
ans.push_back(vector<int>());
int k = q.size();
for (int i = 0; i < k; ++ i)
{
TreeNode* cur = q.front(); q.pop();
ans.back().push_back(cur->val);
if (cur->left) q.push(cur->left);
if (cur->right) q.push(cur->right);
}
}
return ans;
}
};