图神经网络实战（9）——GraphSAGE详解与实现

- 0. 前言
- 1. GraphSAGE 原理
- - 1.1 邻居采样
  - 1.2 聚合
- 2. 构建 GraphSAGE 模型执行节点分类
- - 2.1 数据集分析
  - 2.2 构建 GraphSAGE 模型
- 3. PinSAGE
- 小结
- 系列链接

0. 前言

GraphSAGE 是专为处理大规模图而设计的图神经网络 (Graph Neural Networks, GNN) 架构。在科技行业，可扩展性是推动系统增长的关键驱动力。因此，系统的设计本质上就是为了容纳数百万用户。与图卷积网络 (Graph Convolutional Network, GCN) 和图注意力网络 (Graph Attention Networks，GAT) 相比，这种能力要求从根本上改变 GNN 模型的工作方式。因此，GraphSAGE 自然成为 Uber Eats 和 Pinterest 等科技公司的首选架构。
在本节中，我们将了解 GraphSAGE 的两个主要思想。首先，我们将介绍邻居采样技术，这是 GraphSAGE 可扩展性的核心。然后，我们将探讨用于生成节点嵌入的三种聚合算子。除了原始 GraphSAGE，还将详细介绍 Uber Eats 和 Pinterest 提出的变体架构。最后，使用 PyTorch Geometric 实现 GraphSAGE 架构在 PubMed 数据集上执行节点分类

1. GraphSAGE 原理

Hamilton 等人于 2017 年提出了 GraphSAGE，作为大规模图(节点数超过 10 万)归纳表征学习的框架，其目标是为节点分类等下游任务生成节点嵌入。此外，它还解决了图卷积网络 (Graph Convolutional Network, GCN) 和图注意力网络 (Graph Attention Networks，GAT) 的两个问题——扩展到大规模图和高效泛化到未见过数据。在本节中，我们将通过介绍 GraphSAGE 的两个主要组件来说明如何实现 GraphSAGE：

邻居采样 (Neighbor sampling)
聚合 (Aggregation)

1.1 邻居采样

在传统神经网络中有一个重要概念——小批量 (mini-batch) 训练，通过将数据集划分为更小的片段(称为批，batch )进行训练。梯度下降是一种在训练过程中找到最佳权重和偏置的优化算法。梯度下降有三种类型：

批梯度下降 (Batch gradient descent)：权重和偏置在整个数据集处理完毕后更新(每个 epoch 更新一次)。这是在之前的图卷积网络 (Graph Convolutional Network, GCN) 模型中采用的技术，这种技术训练过程较慢，需要将数据集放在内存中
随机梯度下降 (Stochastic gradient descent)：针对数据集中的每个训练实例更新权重和偏置。由于误差没有进行平均，因此容易受到随机噪声的影响，但可以用于进行在线训练
小批量梯度下降 (Mini-batch gradient descent)：在每个小批量数据训练结束时更新权重和偏置。这种技术训练速度更快(可使用 GPU 并行处理批数据)，收敛也更稳定。此外，对于许多实际的业务场景数据而言，图的规模往往是十分巨大的，数据集往往会超出可用内存，为此采用小批量的训练方式对于大规模图数据的训练是十分必要的

在实践中， RMSprop 或 Adam 等优化器也实现了小批量处理。表格数据集的拆分非常简单，只需选择样本即可。然而，对于图数据集来说，问题在于如何在不破坏基本连接的情况下选择节点。若操作不当，可能会得到一个孤立节点的集合，无法进行任何聚合。
回顾图神经网络 (Graph Neural Networks, GNN) 模型，每个 GNN 层都会根据节点的邻居计算节点嵌入，这意味着计算一个嵌入只需要这个节点的直接邻居( 1 跳)；如果 GNN 有两个 GNN 层，就同时需要它们邻居的邻居( 2 跳)，以此类推，如下所示，图中的其他部分对计算中心节点的嵌入并无关系：

邻居采样

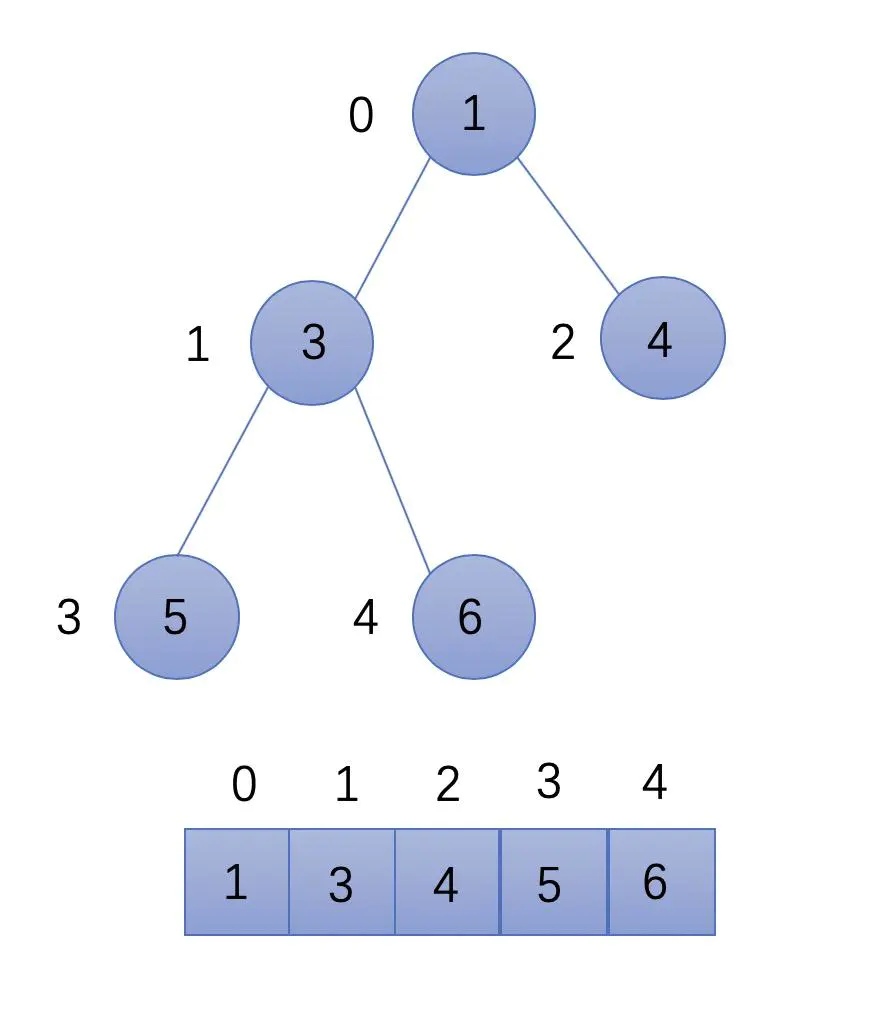
利用这种技术，我们可以用计算图( computation graphs，或称子图)来填充批数据，计算图描述了计算节点嵌入的整个操作序列，下图以更直观的方式展示了节点 0 的计算图：

计算图

根据以上阐述，我们需要聚合 2 跳邻居，以计算 1 跳邻居的嵌入，但是对于一个大规模的图数据而言，直接使用这种设计存在以下两个问题：

计算图随着跳数的增加而呈指数级增长，这会导致很高的计算复杂度
度非常高的节点(如在线社交网络中的名人)，也称为中心节点 (hub node) 或超级节点，会产生巨大的计算图

为了解决这些问题，必须限制计算图的大小。在 GraphSAGE 中，使用邻居采样技术来控制计算图的增长率。具体做法如下：不添加计算图中的每个邻居，而是对预定数量的邻居进行抽样。例如，在第一跳时只保留(最多)三个邻居，在第二跳时只保留五个邻居，因此，在这种情况下，计算图总节点数不会超过 3 × 5 = 15 个节点。

邻居采样

采样数越少，效率越高，但训练的随机性越大(方差越大)。此外，GNN 层数(跳数)必须保持较低水平，以避免计算图呈指数级增长。邻居采样可以处理大规模计算图，但它需要对重要信息进行剪枝处理，从而对准确率等产生负面影响。需要注意的是，计算图涉及大量冗余计算，这会降低整个过程的计算效率。
随机抽样并不是唯一可用的技术。Pinterest 改进了 GraphSAGE 架构，用于构建推荐系统，称为 PinSAGE。PinSAGE 使用随机游走实现了另一种抽样方法，PinSAGE 保留了邻居数量固定的理念，但通过随机行走来检查哪些节点是最常遇到的，这种频率决定了节点的相对重要性。PinSAGE 的采样策略可以选择图中最重要的节点，实践证明，这种方法更加高效。

1.2 聚合

了解了如何选择相邻节点后，还需要计算嵌入。GraphSAGE 研究了聚合邻居操作所需的性质，并提出了几种新的聚合操作 (aggregator，也称聚合算子)：

平均聚合算子
长短期记忆 (long short-term memory, LSTM) 聚合算子
池化聚合算子

平均聚合算子取目标节点及其采样邻居的嵌入平均值，然后，用权重矩阵 $W$ 对这一结果进行线性变换。平均聚合算子可以用以下公式概括，其中 $\sigma$ 是一个非线性函数，如 ReLU 或 tanh：
$h'_i=\sigma(W\cdot mean_{j\in\mathcal N_i}(h_j))$
在 PyTorch Geometric 的 GraphSAGE 实现中，使用了两个权重矩阵，第一个专门用于目标节点，第二个用于邻居节点，因此聚合算子可以改写为：
$h'_i=\sigma(W_1h_i+W_2\cdot mean_{j\in\mathcal N_i}(h_j))$
长短期记忆 (long short-term memory, LSTM) 聚合算子基于长短期记忆 (long short-term memory, LSTM) 架构，LSTM 是一种流行的递归神经网络类型。与平均聚合算子相比，LSTM 聚合算子理论上可以区分更多的图结构，从而产生更好的嵌入。问题在于，递归神经网络只考虑输入的序列，例如一个有开头和结尾的句子。然而，节点没有任何序列，可以通过对节点的邻居进行随机排序解决这一问题。这种解决方法使我们能够使用 LSTM 架构，而无需依赖任何输入序列。
池化聚合算子分为两步工作。首先，将每个邻居的嵌入信息输入多层感知机 (Multilayer Perceptron, MLP)，生成一个新的向量。然后，借鉴了卷积神经网络 (Convolutional Neural Network, CNN) 中的池化操作进行聚合，常见的如最大池化操作，即只保留每个特征的最高值。
除了这三种聚合算子外，还可以在 GraphSAGE 框架中使用其他聚合器。事实上，GraphSAGE 的核心思想主要在于其高效的邻居采样。

2. 构建 GraphSAGE 模型执行节点分类

在本节中，我们将实现 GraphSAGE 架构在 PubMed 数据集上执行节点分类。
我们已经了解了同属 Planetoid 系列的另外两个引文网络数据集——Cora 和 CiteSeer。而 PubMed 数据集则是一个类似网络，但其具有更大的规模，包含 19,717 个节点和 88,648 条边。下图展示了 Gephi 创建的 PubMed 数据集的可视化结果。

PubMed 数据集

PubMed 中节点的特征是 500 维的 TF-IDF (term frequency–inverse document frequency)加权单词向量，我们的目标是将节点正确分为三类——实验性糖尿病 (diabetes mellitus experimental)、1 型糖尿病 (diabetes mellitus type 1) 和 2 型糖尿病 (diabetes mellitus type 2)。接下来，使用 PyTorch Geometric (PyG) 逐步构建 GraphSAGE 实现节点分类。

2.1 数据集分析

(1) 从 Planetoid 类中加载 PubMed 数据集，并打印图数据的相关信息：

from torch_geometric.datasets import Planetoid

dataset = Planetoid(root='.', name="Pubmed")
data = dataset[0]

# Print information about the dataset
print(f'Dataset: {dataset}')
print('-------------------')
print(f'Number of graphs: {len(dataset)}')
print(f'Number of nodes: {data.x.shape[0]}')
print(f'Number of features: {dataset.num_features}')
print(f'Number of classes: {dataset.num_classes}')

# Print information about the graph
print(f'\nGraph:')
print('------')
print(f'Training nodes: {sum(data.train_mask).item()}')
print(f'Evaluation nodes: {sum(data.val_mask).item()}')
print(f'Test nodes: {sum(data.test_mask).item()}')
print(f'Edges are directed: {data.is_directed()}')
print(f'Graph has isolated nodes: {data.has_isolated_nodes()}')
print(f'Graph has loops: {data.has_self_loops()}')

输出结果如下所示：

数据集信息

可以看到，图中有 1000 个测试节点，而只有 60 个训练节点。由于只有 19,717 个节点，用 GraphSAGE 处理 PubMed 的速度非常快。

(2) GraphSAGE 框架的第一步是邻居采样。PyG 使用 NeighborLoader 类来完成这一任务，我们保留目标节点的 10 个邻居和其邻居的 10 个邻居。对 60 个目标节点进行分组，每 16 个节点为一批，最后得到四批数据：

from torch_geometric.loader import NeighborLoader
from torch_geometric.utils import to_networkx

# Create batches with neighbor sampling
train_loader = NeighborLoader(
    data,
    num_neighbors=[5, 10],
    batch_size=16,
    input_nodes=data.train_mask,
)

(3) 通过打印批数据信息，可以验证是否得到四批数据：

# Print each subgraph
for i, subgraph in enumerate(train_loader):
print(f'Subgraph {i}: {subgraph}')

批数据

(4) 每个子图包含 60 多个节点，使用 matplotlib 的 subplot 将它们绘制成图像：

import numpy as np
import networkx as nx
import matplotlib.pyplot as plt

# Plot each subgraph
fig = plt.figure(figsize=(16,16))
for idx, (subdata, pos) in enumerate(zip(train_loader, [221, 222, 223, 224])):
    G = to_networkx(subdata, to_undirected=True)
    ax = fig.add_subplot(pos)
    ax.set_title(f'Subgraph {idx}', fontsize=24)
    plt.axis('off')
    nx.draw_networkx(G, pos=nx.spring_layout(G), with_labels=False, node_color=subdata.y)
plt.show()

计算图

从上图可以看到，由于采用邻居抽样，子图中大多数节点的度数都是 1。因为它们的嵌入只在计算图中使用一次，以计算第二层的嵌入。

2.2 构建 GraphSAGE 模型

(1) 实现 accuracy() 函数评估模型的准确性：

import torch
import torch.nn.functional as F
from torch_geometric.nn import SAGEConv

def accuracy(pred_y, y):
    """Calculate accuracy."""
	return ((pred_y == y).sum() / len(y)).item()

(2) 使用两个 SAGEConv 层初始化 GraphSAGE 类(默认选择平均聚合算子)：

class GraphSAGE(torch.nn.Module):
    """GraphSAGE"""
    def __init__(self, dim_in, dim_h, dim_out):
        super().__init__()
        self.sage1 = SAGEConv(dim_in, dim_h)
        self.sage2 = SAGEConv(dim_h, dim_out)

(3) 使用两个平均聚合算子计算嵌入，并使用一个非线性函数 (ReLU) 和一个 Dropout 层：

    def forward(self, x, edge_index):
        h = self.sage1(x, edge_index)
        h = torch.relu(h)
        h = F.dropout(h, p=0.5, training=self.training)
        h = self.sage2(h, edge_index)
        return h

(4) 由于采用小批量训练，fit() 函数需要修改为先循环 epoch 次，然后再循环批数据，以在每个批数据上训练 epoch 次，模型的度量指标必须在每个 epoch 开始时重新初始化：

    def fit(self, loader, epochs):
        criterion = torch.nn.CrossEntropyLoss()
        optimizer = torch.optim.Adam(self.parameters(), lr=0.01)

        self.train()
        for epoch in range(epochs+1):
            total_loss = 0
            acc = 0
            val_loss = 0
            val_acc = 0

第二个循环在每个批数据上训练模型：

            for batch in loader:
                optimizer.zero_grad()
                out = self(batch.x, batch.edge_index)
                loss = criterion(out[batch.train_mask], batch.y[batch.train_mask])
                total_loss += loss.item()
                acc += accuracy(out[batch.train_mask].argmax(dim=1), batch.y[batch.train_mask])
                loss.backward()
                optimizer.step()

                # Validation
                val_loss += criterion(out[batch.val_mask], batch.y[batch.val_mask])
                val_acc += accuracy(out[batch.val_mask].argmax(dim=1), batch.y[batch.val_mask])

打印模型训练过程模型性能的变化情况：

            if epoch % 20 == 0:
                print(f'Epoch {epoch:>3} | Train Loss: {loss/len(loader):.3f} | Train Acc: {acc/len(loader)*100:>6.2f}% | Val Loss: {val_loss/len(train_loader):.2f} | Val Acc: {val_acc/len(train_loader)*100:.2f}%')

(5) 实现 test() 方法，测试集不使用小批量进行测试：

    @torch.no_grad()
    def test(self, data):
        self.eval()
        out = self(data.x, data.edge_index)
        acc = accuracy(out.argmax(dim=1)[data.test_mask], data.y[data.test_mask])
        return acc

(6) 实例化一个隐藏维度为 64 的模型，并对其进行 200 个 epoch 的训练：

# Create GraphSAGE
graphsage = GraphSAGE(dataset.num_features, 64, dataset.num_classes)
print(graphsage)

# Train
graphsage.fit(train_loader, 200)

训练过程

需要注意的是，两个 SAGEConv 层都使用默认的平均聚合算子。

(7) 最后，在测试集上对训练后的模型进行测试：

acc = graphsage.test(data)
print(f'GraphSAGE test accuracy: {acc*100:.2f}%')

# GraphSAGE test accuracy: 75.90%

可以看到，模型在测试集上的准确率为 75.90%，考虑到此数据集的训练/测试的分割方式并非最佳，这已经算是一个不错的成绩。虽然，在 PubMed 数据集上，GraphSAGE 的平均准确率低于图卷积网络 (Graph Convolutional Network, GCN) (76.2%) 和图注意力网络 (Graph Attention Networks，GAT) (77.12%)，但在训练这三个模型时，我们可以感受到了 GraphSAGE 的训练速度极快。使用 GPU 进行训练，GraphSAGE 的训练速度比 GCN 快 4 倍，比 GAT 快 88 倍。即使 GPU 的内存不是问题，GraphSAGE 在处理大规模的图数据时也能得到更好的结果。
我们还可以使用无监督学习，在没有标签的情况下训练 GraphSAGE。这在标签缺失或标签由下游应用程序提供的情况下十分有用，但这种情况下需要使用新的损失函数，以鼓励相近的节点有相似的表示，同时确保相距较远的节点的嵌入也具有较大距离：
$J_\mathcal G(h_i)=-log(\sigma(h_i^Th_j))-Q\cdot E_{j_n\sim P_n(j)}log(\sigma(-h_i^Th_{j_n}))$
其中， $j$ 是随机行走中 $u$ 的邻居， $σ$ 是 sigmoid 函数， $P_n(j)$ 是 $j$ 的负采样分布， $Q$ 是负采样的数量。
除了 GraphSAGE 外，还可以考虑采用其它方式扩展 GNN，以如下两种标准技术为例：

Cluster-GCN 对于如何创建小批量数据提供了不同的解决方案。它并未采用邻居采样，而是将图划分为孤立的集群，然后将这些集群作为独立的图进行处理，这可能会对生成的嵌入的质量产生负面影响
简化 GNN 可以缩短训练和推理时间。在实践中，简化方法包括舍弃非线性激活函数，线性层可以通过线性代数压缩成一个矩阵乘法。当然，这些简化 GNN 在小数据集上不如完整的 GNN 准确，但在大规模图(如 Twitter )上十分高效。

3. PinSAGE

PinSAGE 是基于 GraphSAGE 的推荐系统，将无监督学习与最大间隔排名损失 (max-margin ranking loss) 函数结合起来。目标是为每个用户排列出最相关的实体(食物、餐馆、标记等)，为了实现这一目标，采用最大间隔排名损失函数(通过比较正样本和负样本之间的嵌入向量来度量它们之间的相似性)，并考虑了嵌入对。
具体而言，对于每个用户，PinSAGE 选择一个正样本（例如用户喜欢的实体）和多个负样本（例如用户不感兴趣的实体）。然后，它计算正样本嵌入向量与每个负样本嵌入向量之间的差异，并通过最大化它们之间的间隔来优化模型。这种损失函数的目的是鼓励模型将正样本与负样本区分开来，以便在推荐过程中能够更好地排名最相关的实体。

小结

本节介绍了 GraphSAGE 框架及其两个组成部分——邻居采样算法和三个不同的聚合算子，其中邻居采样是 GraphSAGE 能够高效处理大规模图的核心。并使用 PyTorch Geometric 构建 GraphSAGE 模型在 PubMed 数据集上执行节点分类，GraphSAGE 虽然准确率略低于 GCN 或 GAT 模型，但它是常用于处理大规模图数据的高效框架。

系列链接

图神经网络实战（1）——图神经网络(Graph Neural Networks, GNN)基础
图神经网络实战（2）——图论基础
图神经网络实战（3）——基于DeepWalk创建节点表示
图神经网络实战（4）——基于Node2Vec改进嵌入质量
图神经网络实战（5）——常用图数据集
图神经网络实战（6）——使用PyTorch构建图神经网络
图神经网络实战（7）——图卷积网络(Graph Convolutional Network, GCN)详解与实现
图神经网络实战（8）——图注意力网络(Graph Attention Networks, GAT)