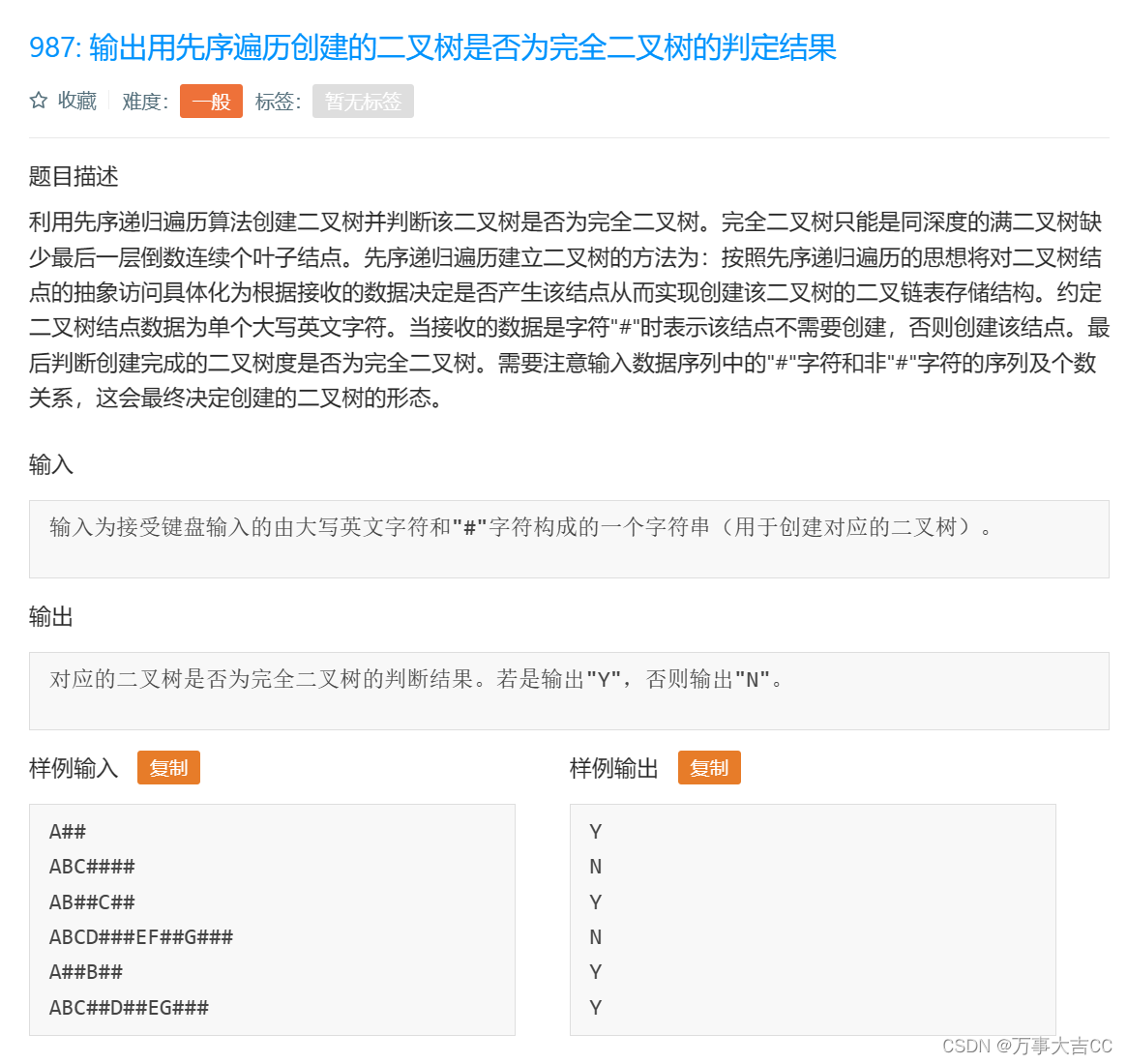
解法：

一棵二叉树是完全二叉树的条件是：

1. 对于任意一个结点，如果它有右子树而没有左子树，则这棵树不是完全二叉树。

2. 如果一个结点有左子树但是没有右子树，则这个结点之后的所有结点都必须是叶子结点。

如果满足以上条件，则这棵二叉树是完全二叉树；否则，不是完全二叉树。

图解：

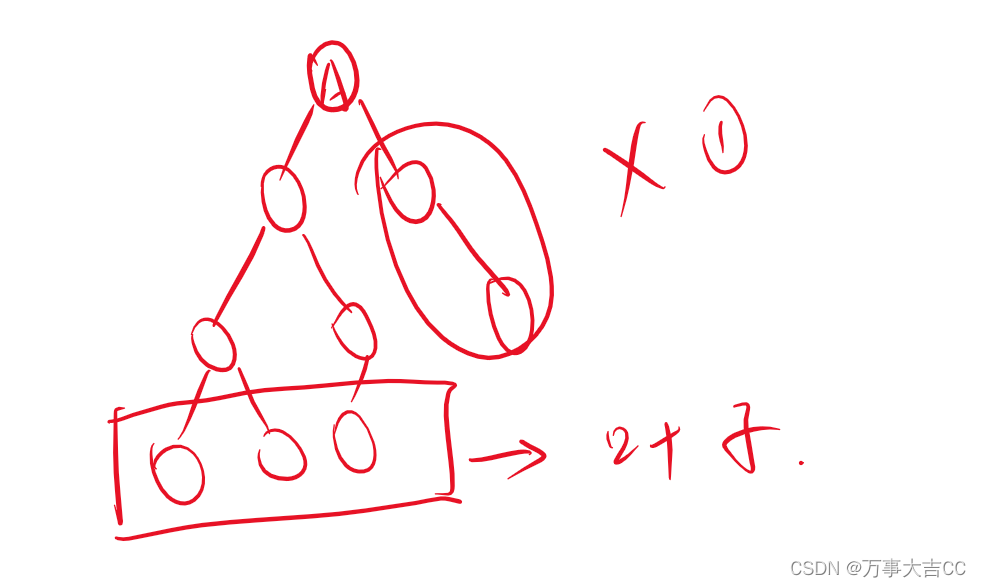
980: 输出利用先序遍历创建的二叉树的层次遍历序列_swust oj 980: 输出利用先序遍历创建的二叉树的层次遍历序列-CSDN博客

和这道题是一样的，在这基础上补二个判断即可

#include<iostream>
#include<queue>
using namespace std;
struct treeNode {
	char val;
	treeNode* left;
	treeNode* right;
	treeNode(char x) :val(x), left(NULL), right(NULL) {};
};
treeNode* buildTree() {
	char ch;
	cin >> ch;
	if (ch == '#') return NULL;
	treeNode* root = new treeNode(ch);
	root->left = buildTree();
	root->right = buildTree();
	return root;
}
bool bfs(treeNode* root) {
	queue<treeNode*> q;
	if (root == NULL) return false;
	q.push(root);
	int flag = 0;
	while (!q.empty()) {
		int num = q.size();
		for (int i = 0; i < num; i++) {
			treeNode* cur = q.front();
			q.pop();
			if (flag) {
				if (cur->left || cur->right)
					return false;
			}
			if (cur->right && cur->left == NULL) return false;
			if (cur->left && cur->right == NULL) flag = 1;
			
			if (cur->left) q.push(cur->left);
			if (cur->right) q.push(cur->right);
		}
	}
	return true;
}
int main() {
	treeNode* root = buildTree();
	if (bfs(root)) {
		cout << "Y";
	}
	else cout << "N";
	return 0;
}