最终达到的效果:
调用一个类
class HuffmanCodin{.....}
使用类中的静态方法,获取哈夫曼编码:

事前准备——哈夫曼树的节点定义
class Node implements Comparable<Node> {
int weight;//权重
Node left;
Node right;
char ch;//关键字,字符
String code;//相应的哈夫曼编码
public Node(char ch, int weight) {//构造方法,键值对
this.weight = weight;
this.ch = ch;
}
//构造方法,只设置出现频率
public Node(int weight) {
this.weight = weight;
}
//重写compareTo方法
@Override
public int compareTo(Node node) {
if(this.weight - node.weight==0){//如果两个字符出现的频率一样,那么就比较字典序(两个字符一定是不同的)
return this.ch-node.ch;
}
return this.weight - node.weight;//默认排列升序
}
//重写toString方法
//效果:[ 字符 -> 010 ]
@Override
public String toString() {//重写之后,等一下打印就可以直接用引用就可以了
return "[" + this.ch + " -> " + this.code + "] ";
}
}步骤:
想要达到上述效果,大致可以分为这几步:
1、字符集转化成一个一个的键值对;
2、键值对转节点,节点放入一个集合
3、依据集合创建哈夫曼树。
4、对哈夫曼树的叶子节点进行哈夫曼编码
下面我们一点一点来解决
1、字符集转键值对
这里就要使用到HashMap了:
HashMap的
Key=一个字符
Value=权重(就是一个字符在字符集出现的频率,当然也不完全是,等一下会讲到)
public class Test {
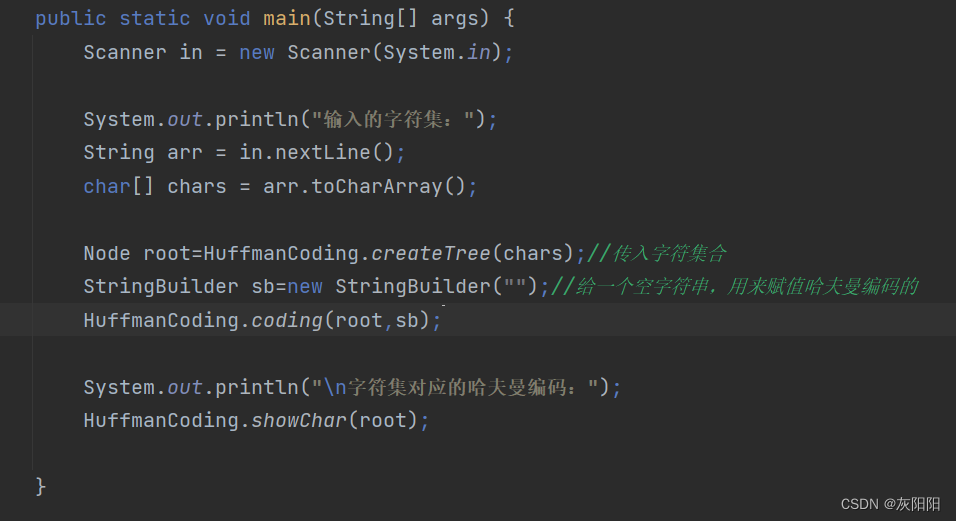
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.println("输入的字符集:");
String arr = in.nextLine();
char[] chars = arr.toCharArray();//转化成字符数组
Node root=HuffmanCoding.createTree(chars);//调用这个静态方法,具体实现看下一块代码
}
}class HuffmanCoding {
public static Node createTree(char[] arr) {
Map.Entry<Character, Integer>[] entries = charGetEntry(arr);//获取键值对
}charGetEntry()方法就是专门用来把字符集转化成一个一个的键值对的,然后返回这个类型:
Map.Entry<Character, Integer>[]
为什么是这个类型?
因为HashMap不能直接同时访问Character也就是字符,以及Integer接也就是对应字符的权重。
如果要访问键值对,需要调用HashMap的setEntry方法,setEntry方法会返回Map.Entry<Character, Integer>[]类型的数组
而Map.Entry中有访问和修改关键字和值的方法。
charGetEntry()方法:
private static Map.Entry<Character, Integer>[] charGetEntry(char[] arr) {
//定义Hashmap储存不重复的键值对
Map<Character, Integer> map = new HashMap<>(arr.length);//长度肯定不会超过arr的长度
for (char ch : arr) {
map.put(ch, 0);//权值默认先给0,等一下处理
}
//定义Entry[]这个集合,用来存放键值对
Map.Entry<Character, Integer>[] entrys = new Map.Entry[map.size()];//长度刚好就是map的长度
int i = 0;
for (Map.Entry<Character, Integer> entry : map.entrySet()) {//遍历每一个entry,以此把每一个键值对放到集合entrys中
entrys[i++] = entry;
}
//现在就可以赋值weight了
i=entrys.length-1;//从后往前遍历,当然从前往后也可以
while(i>=0){
int n=0;
for (int j = 0; j <arr.length ; j++) {
if(entrys[i].getKey()==arr[j]){//两个字符一样,那么频率++
n++;
}
}
entrys[i--].setValue(n);
}
//程序到达这里,键值对已经储存完毕,下面直接返回集合即可
return entrys;
}如下第一步完成:

2、键值对转节点
上一步我们已经获得了所有的键值对,储存在entries中,现在只需创建一个List<Node>类型的集合,获遍历entries,获取键值对即可:
//放入节点中(用集合来管理)
int length = entries.length;
List<Node> nodeList = new ArrayList<>(length);//长度一定和entries是一样的
while (length > 0) {
//用Node的构造方法,创建结点,第一个参数是关键子,第二个参数是权重
nodeList.add(new Node(entries[length - 1].getKey(), entries[length - 1].getValue()));
length--;
}
此时,第二步完成,nodeList就是一个储存着所有结点的集合。
3、构造哈夫曼树
此时类
HuffmanCoding
的静态方法createTree已经定义好了:
public static Node createTree(char[] arr) {
Map.Entry<Character, Integer>[] entries = charGetEntry(arr);//获取键值对,已经完成,保存在了entries中
//放入节点中(用集合来管理)
int length = entries.length;
List<Node> nodeList = new ArrayList<>(length);//长度一定和entries是一样的
while (length > 0) {
nodeList.add(new Node(entries[length - 1].getKey(), entries[length - 1].getValue()));
length--;
}
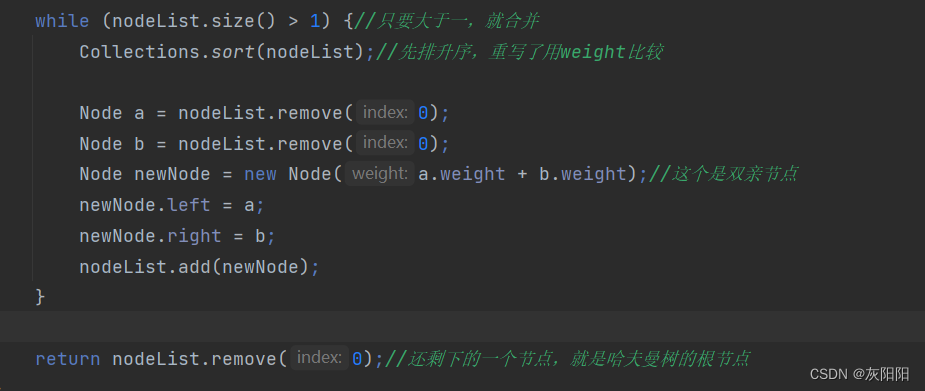
while (nodeList.size() > 1) {//只要大于一,就合并
Collections.sort(nodeList);//先排升序,重写了用weight比较
Node a = nodeList.remove(0);
Node b = nodeList.remove(0);
Node newNode = new Node(a.weight + b.weight);//这个是双亲节点
newNode.left = a;
newNode.right = b;
nodeList.add(newNode);
}
return nodeList.remove(0);//还剩下的一个节点,就是哈夫曼树的根节点
}
4、叶结点编码
下面运用的是递归,对叶子结点进行赋值0或者1(左结点是0,右结点时1):
//这个函数可以把Node的code修改
public static void coding(Node root, StringBuilder sb) {
if (root == null) return;//如果只有一个节点,code==“”---->空字符串
root.code = sb.toString();//先根节点
if (root.left == null && root.right == null) {
return;//直接返回
}
//如果不是叶子节点,那么一定有左右孩子----》因为这是哈夫曼树
sb.append("0");//先左边,所以加一个0
coding(root.left, sb);//递归
sb.replace(sb.length() - 1, sb.length(), "1");//把最后一个替换成1,因为要走右边了
coding(root.right, sb);//递归
sb.delete(sb.length() - 1, sb.length());//也要删除,删除的区间是:左开右闭的!
}现在这个HuffmanCoding这个类就可以对一个字符集进行哈夫曼编码了,当然如果想要打印对应的值,需要写一个打印叶子结点的方法:
//前序遍历打印叶子结点
public static void showChar(Node root) {
if (root == null) return;
if (root.left == null && root.right == null) {//这是一个叶子节点,直接打印然后返回
System.out.println(root);
return;
}
//不是叶子结点,就遍历左右子树
showChar(root.left);
showChar(root.right);
}测试
最终哈夫曼编码类的源码:
class HuffmanCoding {
public static Node createTree(char[] arr) {
Map.Entry<Character, Integer>[] entries = charGetEntry(arr);//获取键值对,已经完成,保存在了entries中
//放入节点中(用集合来管理)
int length = entries.length;
List<Node> nodeList = new ArrayList<>(length);//长度一定和entries是一样的
while (length > 0) {
nodeList.add(new Node(entries[length - 1].getKey(), entries[length - 1].getValue()));
length--;
}
while (nodeList.size() > 1) {//只要大于一,就合并
Collections.sort(nodeList);//先排升序,重写了用weight比较
Node a = nodeList.remove(0);
Node b = nodeList.remove(0);
Node newNode = new Node(a.weight + b.weight);//这个是双亲节点
newNode.left = a;
newNode.right = b;
nodeList.add(newNode);
}
return nodeList.remove(0);//还剩下的一个节点,就是哈夫曼树的根节点
}
private static Map.Entry<Character, Integer>[] charGetEntry(char[] arr) {
//定义Hashmap储存不重复的键值对
Map<Character, Integer> map = new HashMap<>(arr.length);//长度肯定不会超过arr的长度
for (char ch : arr) {
map.put(ch, 0);//权值默认先给0,等一下处理
}
//定义Entry[],又来放键值对(可以访问的)
Map.Entry<Character, Integer>[] entrys = new Map.Entry[map.size()];//长度刚好就是map的长度
int i = 0;
for (Map.Entry<Character, Integer> entry : map.entrySet()) {
entrys[i++] = entry;
}
//先在赋值weight
i=entrys.length-1;
while(i>=0){
int n=0;
for (int j = 0; j <arr.length ; j++) {
if(entrys[i].getKey()==arr[j]){//两个字符一样,那么频率佳佳
n++;
}
}
entrys[i--].setValue(n);
}
//程序到达这里,键值对已经储存完毕
return entrys;
}
//这个函数可以把Node的code修改
public static void coding(Node root, StringBuilder sb) {
if (root == null) return;//如果只有一个节点,code==“”---->空字符串
root.code = sb.toString();//先根节点
if (root.left == null && root.right == null) {
return;//直接返回
}
//如果不是叶子节点,那么一定有左右孩子----》因为这是哈夫曼树
sb.append("0");//先左边,所以加一个0
coding(root.left, sb);//递归
sb.replace(sb.length() - 1, sb.length(), "1");//把最后一个替换成1,因为要走右边了
coding(root.right, sb);//递归
sb.delete(sb.length() - 1, sb.length());//也要删除,删除的区间是:左开右闭的!
}
//前序遍历打印叶子结点
public static void showChar(Node root) {
if (root == null) return;
if (root.left == null && root.right == null) {//这是一个叶子节点,直接打印然后返回
System.out.println(root);
return;
}
//不是叶子结点,就遍历左右子树
showChar(root.left);
showChar(root.right);
}
}
类中静态方法使用的演示:
关于哈夫曼编码的解码
会了编码,其实解码就很容易了
值得注意的是:
不同的字符集合,对应的哈夫曼编码是有所差异的
所以如果要进行解码,那么必须直到每一个字符对应出现的频率
解码思路:
在接收到字符频度表之后,创建一颗哈夫曼树,每次从root结点开始遍历,从第一个字符开始,是0就往左树走,是1就往右走,直到叶子结点即可解码。
具体实现:
public static void deCoding(Map.Entry<Character, Integer>[] arrEntry, String arr) {//需要接收字符频度表 and 哈夫曼编码
Node Cur= createTree(arrEntry);//调用了重载的创建哈夫曼树的方法
char[] chars = arr.toCharArray();
int cur = 0;//表示读取编码的位置
Node root=Cur;//Cur保存了哈夫曼树的根结点
while (cur < chars.length) {//读完就退出循环
while (root.left != null && root.right != null) {//没有到叶子结点就一直循环
if (chars[cur] == '1') {//是1走右边
cur++;
root = root.right;
} else {//是二走左边
cur++;
root = root.left;
}
}
//如果跳出了循环说明已经是叶子结点了
System.out.println(root);
root=Cur;
}
}
因为我们在createTree()方法中传入的类型是Map.Entry<Character, Integer>[],
所以需要对createTree()方法,
进行一次重载,
这个重载其实不麻烦,只要改一下接口,就可以了:
private static Node createTree(Map.Entry<Character, Integer>[] entries){//重载方法,用在解码时调用这个方法
//放入节点中(用集合来管理)
int length = entries.length;//只改了这一行,和方法的唯一参数!!!!!
List<Node> nodeList = new ArrayList<>(length);//长度一定和entries是一样的
while (length > 0) {
nodeList.add(new Node(entries[length - 1].getKey(), entries[length - 1].getValue()));
length--;
}
while (nodeList.size() > 1) {//只要大于一,就合并
Collections.sort(nodeList);//先排升序,重写了用weight比较
Node a = nodeList.remove(0);
Node b = nodeList.remove(0);
Node newNode = new Node(a.weight + b.weight);//这个是双亲节点
newNode.left = a;
newNode.right = b;
nodeList.add(newNode);
}
return nodeList.remove(0);//还剩下的一个节点,就是哈夫曼树的根节点
}