【动态规划】：路径问题

【动态规划】：路径问题_地下城游戏

news2024/11/18 15:33:48

朋友们、伙计们，我们又见面了，本专栏是关于各种算法的解析，如果看完之后对你有一定的启发，那么请留下你的三连，祝大家心想事成！

C 语言专栏：C语言：从入门到精通

数据结构专栏：数据结构

个人主页：stackY、

C + + 专栏：C++

Linux 专栏：Linux

1. 题目解析

2. 算法原理

2.1 状态表示

2.2 状态转移方程

2.3 初始化

2.4 填表顺序

2.5 返回值

3. 代码实现

4. 算法复杂度

1. 题目解析

LeetCode174.地下城游戏：https://leetcode.cn/problems/dungeon-game/description/https://leetcode.cn/problems/dungeon-game/description/

174. 地下城游戏

恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里，他必须穿过地下城并通过对抗恶魔来拯救公主。

骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。

有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

为了尽快解救公主，骑士决定每次只向右或向下移动一步。

返回确保骑士能够拯救到公主所需的最低初始健康点数。

注意：任何房间都可能对骑士的健康点数造成威胁，也可能增加骑士的健康点数，包括骑士进入的左上角房间以及公主被监禁的右下角房间。

示例 1：
输入：dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
输出：7
解释：如果骑士遵循最佳路径：右 -> 右 -> 下 -> 下 ，则骑士的初始健康点数至少为 7 。
示例 2：
输入：dungeon = [[0]]
输出：1
提示：

m == dungeon.length
n == dungeon[i].length
1 <= m, n <= 200
-1000 <= dungeon[i][j] <= 1000

该题是一个二维的路径问题，根据题目描述，每次只能走一步，并且只能向下或者向右走，在走到该位置时会失去健康值，当健康值为0或者小于0时会死亡，左上角和右下角的位置也会失去对应的健康值，所以，我们需要在不死的前提下确定一个从左上角走到右下角的最小的初始血量。

2. 算法原理

解决路径问题常用的就是动态规划思想：

2.1 状态表示

关于路径问题我们通常是以某一位置为结束再根据题目要求进行表示：

以某一位置为结束：dp[i][j]就表示从开始走到[i, j]位置时所需的最小初始健康点数，如果这样子用来进行状态表示，那么会出现一个问题，要能走到[i, j]位置，还必须要能走到[i, j+1]和[i+1, j]的位置，因为当前位置的血量还会被下边和右边的位置所影响，因此这样表示是不能推出来状态转移方程；所以我们需要用某一开始位置进行定义：

以某一位置为开始：dp[i][j]就表示从[i][j]位置走到达终点时所需要的最小初始健康点数。

2.2 状态转移方程

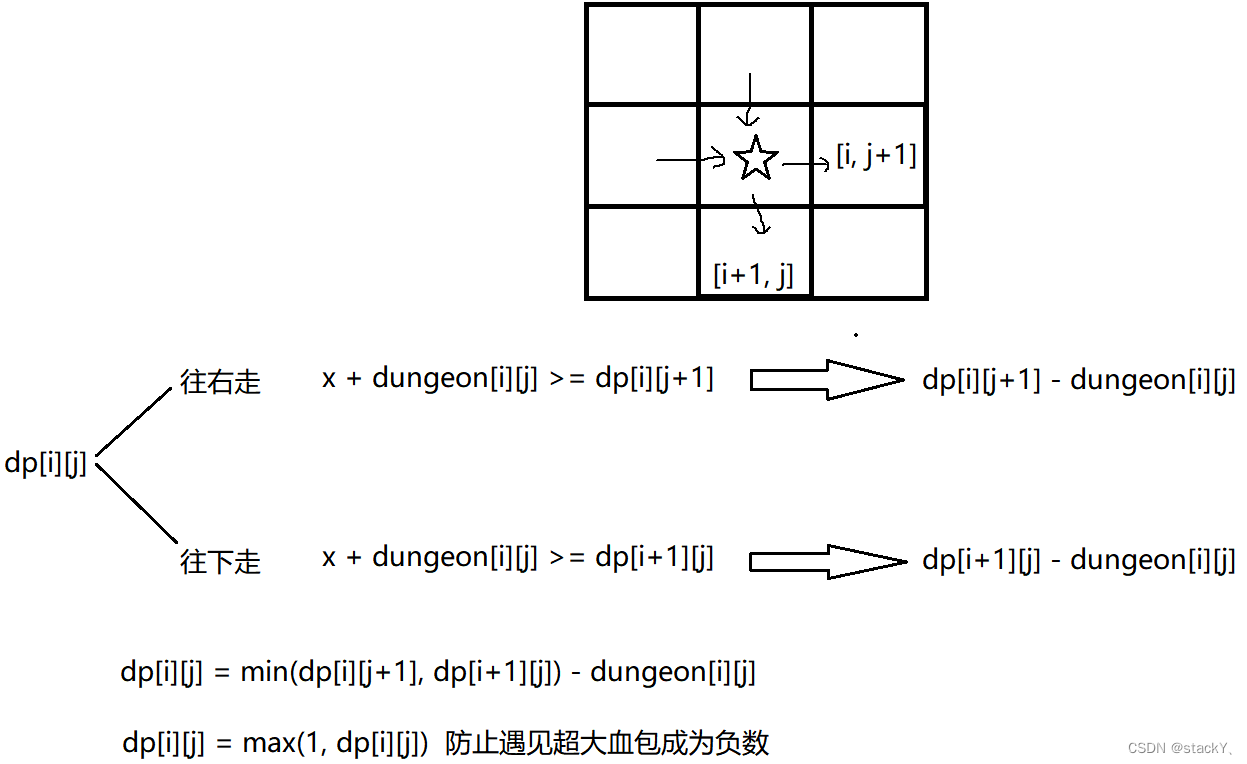
根据状态表示：dp[i][j]表示的是从[i][j]位置走到终点所需要的最小初始健康点数，那么走到

[i, j]位置时，下一步有两种走法：

此时我们就可以假设初始血量为x，

① 向右[i, j+1]走一步，那么x + dungeon[i][j] >= dp[i][j + 1]

② 向下[i+1, j]走一步，那么x + dungeon[i][j] >= dp[i + 1][j]

因为我们需要求最小初始血量，根据上式换算将x换为dp[i][j]即可

dp[i][j] = min(dp[i][j + 1], dp[i + 1][j]) - dungeon[i][j]

此时还存在一个问题，如果dungeon[i][j]是一个非常大的血包，也就是说上面的式子的结果成了负数，此时是不合理的，因为血量小于等于0就死亡了，因此如果遇见上面的情况，我们仅用一滴血就可以到达，所以需要将血量由负数转化为1即可。

dp[i][j] = max(1, dp[i][j])

2.3 初始化

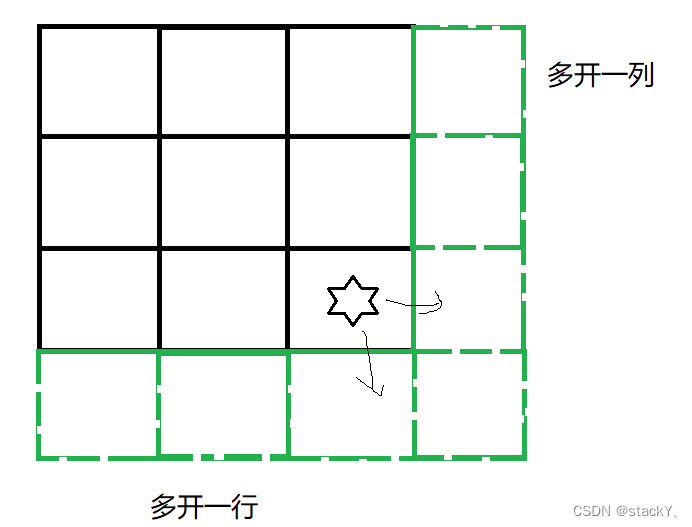
根据状态表示和状态转移方程，我们在填当前位置的值时，需要用到右边的一个或者是下边的一个，那么位于最右边一列和最下面一行在填表时都存在越界的风险，所以我们在最右边一列再加一列，最下面一行再加一行。

那么只需要将多开的这一行，和这一列初始化即可，那么这些位置该怎么初始化呢？

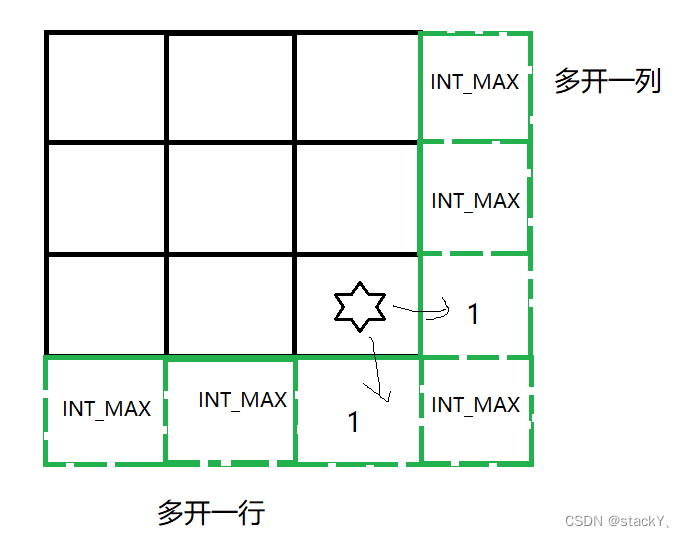
① 先来看带有星星的位置，这个位置就是真实的最后一个位置，那么当我们走到这个位置，我们应该至少存在1滴血，所以它的右边和下边的初始化为1即可；

② 因为我们取的是右边或者下边的较小值，所以剩余位置设置为INT_MAX即可。

为了方便起，我们可以在创建dp表时就将所有的值都初始化为INT_MAX，然后只对特殊的两个位置初始化为1即可。

2.4 填表顺序

因为我们是以[i, j]位置为开始然后进行表述，所以我们的填表顺序应该是从下往上填每一行，每一行中从右往左。

2.5 返回值

根据状态表示，我们最终的返回值是dp[0][0]

3. 代码实现

class Solution 
{
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) 
    {
        int m = dungeon.size();
        int n = dungeon[0].size();
        // 创建dp表
        vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));
        // 初始化
        dp[m - 1][n] = dp[m][n - 1] = 1;
        // 填表
        for(int i = m - 1; i >= 0; i--)
            for(int j = n - 1; j >= 0; j--)
            {
                dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];
                dp[i][j] = max(1, dp[i][j]);
            }
        return dp[0][0];
    }
};