感知机简介
- 导语
- 感知机
- 简单逻辑电路实现
- 权重和配置
- 与/或/与非
- 与门实现
- 与非门实现
- 或门实现
- 线/非线性
- 单/多层感知机
- 异或
- 总结
- 参考文献
导语
学习感知机有助于更好的理解深度学习的神经元、权重等概念,感知机的结构和概念很简单,只要学过基本线性代数、数字电路逻辑就能理解,如果直接学习深度学习的神经元等概念,可能会比较难啃,但是在学过感知机之后,再走入深度学习的殿堂就变得简单了。
感知机
感知机的基本功能是允许接收多个输入信号,随后输出一个信号,有点类似程序设计语言中的函数,现实中比较好理解的例子有很多,比如说74ls138芯片,多路选择器这种,简单的原理如下图。
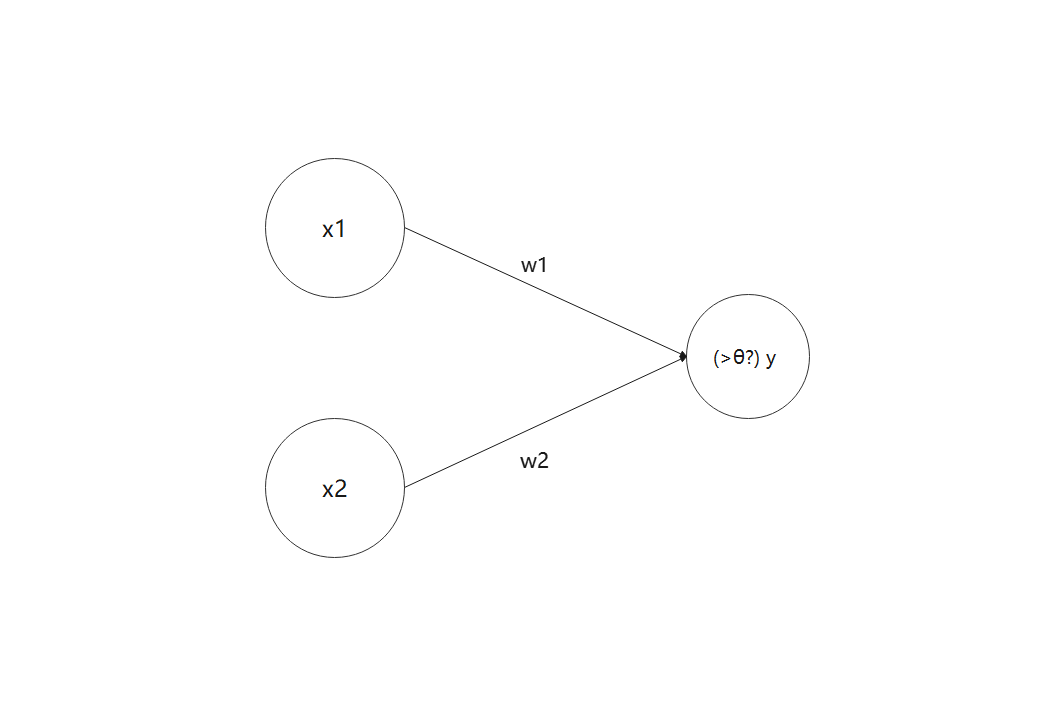
在这个感知机中,
x
1
,
x
2
x_1,x_2
x1,x2作为输入信号,
y
y
y为输出信号,
w
1
,
w
2
w_1,w_2
w1,w2是权重,圆圈为节点,信号输入时会与对应的权重相乘,并将结果累和,当累和值超过阈值
θ
\theta
θ时,
y
y
y才会有输出1,否则为0。
以图论的角度来理解的话,整个感知机是一个有向无环图, x 1 , x 2 x_1,x_2 x1,x2为点权, w 1 , w 2 w_1,w_2 w1,w2为边权, y y y的点权由点权×边权的累和与阈值判断来决定。
将图以数学式子来表示的话,就是下式。
y = { 0 , i f ( w 1 x 1 + w 2 x 2 ≤ θ ) 1 , i f ( w 1 x 1 + w 2 x 2 > θ ) y= \begin{cases} 0,&if &(w_1x_1+w_2x_2\le\theta)\\ 1,&if &(w_1x_1+w_2x_2\gt\theta) \end{cases} y={0,1,ifif(w1x1+w2x2≤θ)(w1x1+w2x2>θ)
权重越大,代表对应输入对最后结果的影响越大。
简单逻辑电路实现
从简单的数字电路逻辑实现来入手有助于对感知机进行理解,在此略过与或非等概念的解释,只给出实现
权重和配置
对于上一部分的式子,如果我们将
θ
\theta
θ移到左边,用一个新的字符
b
b
b来代替,可以发现得到的式子和深度学习所用到的式子非常类似,如下图。
y
=
{
0
,
i
f
(
w
1
x
1
+
w
2
x
2
+
b
≤
0
)
1
,
i
f
(
w
1
x
1
+
w
2
x
2
+
b
>
0
)
y= \begin{cases} 0,&if &(w_1x_1+w_2x_2+b\le0)\\ 1,&if &(w_1x_1+w_2x_2+b\gt 0) \end{cases}
y={0,1,ifif(w1x1+w2x2+b≤0)(w1x1+w2x2+b>0)
b b b在这里被视为偏置,用来修正先前部分计算的结果,按照书上的说法是调整神经元被激活的容易程度,按照我的理解, b b b类似于一种敏感度,一个门槛,当先前部分结果越过了这个门槛,其值才有效。
与/或/与非
下面是书上对各门电路的实现代码,按照自己的编程习惯改了点。
与门实现
import numpy as np
def AND(x1,x2):
x=np.array([x1,x2])
w=np.array([0.6,0.6])#w是可变的
b=-0.8#b也一样
#w=[0.5,0.5],b=-0.7也可
y=np.sum(w*x)+b
if y<=0:
return 0
else:
return 1
print(AND(0,0))
print(AND(0,1))
print(AND(1,0))
print(AND(1,1))

与非门实现
import numpy as np
def NAND(x1,x2):
x=np.array([x1,x2])
w=np.array([-0.6,-0.6])#w是可变的
b=0.8#b也一样
y=np.sum(w*x)+b
if y<=0:
return 0
else:
return 1
print(NAND(0,0))
print(NAND(0,1))
print(NAND(1,0))
print(NAND(1,1))

或门实现
import numpy as np
def OR(x1,x2):
x=np.array([x1,x2])
w=np.array([0.6,0.6])#w是可变的
b=-0.3#b也一样
y=np.sum(w*x)+b
if y<=0:
return 0
else:
return 1
print(OR(0,0))
print(OR(0,1))
print(OR(1,0))
print(OR(1,1))

线/非线性
在实现前面的各种门电路的时候,可以发现能够满足最后输出的权重值和偏置值是有多组的,为了更好的解释这个问题,书上结合了高中数学的线性规划知识点,用了一个非常巧妙的方法来解释这个问题,以或门的输出为例,具体如下图。
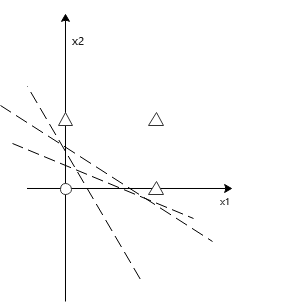
假设以
x
1
x_1
x1为横坐标,
x
2
x_2
x2为纵坐标,图中三角形为输出为1的情况,圆形为输出为0的情况,可以清楚的看到,以虚线
l
l
l为分界线(即
b
+
w
1
∗
x
1
+
w
2
∗
x
2
=
0
b+w_1*x1+w_2*x2=0
b+w1∗x1+w2∗x2=0)时,虚线正好把所有输出为0和输出为1的情况分开了,也就是说,构成了一个可以由一条直线分割的线性空间,通常情况下,这条直线是不唯一的,这也解释了偏置值和权重值存在多组的原因。
在实现了与门等简单电路后,我们可以探讨如何实现异或门,异或门是否也能像前三个一样实现?以异或门的输出构造的图如下。
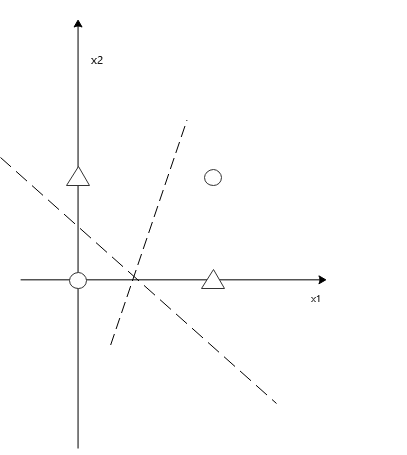
可以发现,无论取怎样的直线,都不可能将1和0的情况完全分割开了,这个时候,直线已经无法分割了,也就是说不存在可用的线性空间了。
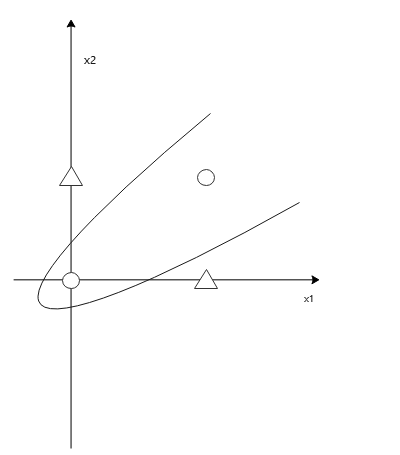
一计不成再生一计,当我们使用曲线时,就会发现,存在一个曲线能够将0和1的情况分割开来,与直线相对应的,即存在一个可用曲线分割的非线性空间。
单/多层感知机
到这里,异或和感知机似乎无缘了,但是如果学习过数字电路逻辑就知道,异或是可以通过与门这些门电路进行实现的,在感知机上的具体体现,就是感知机可以通过“叠加层”来实现更复杂的结构。
像上述实现与门、或门这些的感知机,被称为单层感知机,因其输入输出间只有一层而得名,更具体来说,是因为单层感知机只能分割线性空间,而不能分割非线性空间,与单层感知机相对应的是多层感知机,输入输出间存在多层,可以分割非线性空间。
书中提到,理论上2层感知机可以表示任意函数(激活函数使用sigmod的感知机)。
异或
根据数字电路的知识,可以在与、或、与非门的基础上实现异或门,具体如下。
import numpy as np
def OR(x1,x2):
x=np.array([x1,x2])
w=np.array([0.6,0.6])#w是可变的
b=-0.3#b也一样
y=np.sum(w*x)+b
if y<=0:
return 0
else:
return 1
def NAND(x1,x2):
x=np.array([x1,x2])
w=np.array([-0.6,-0.6])#w是可变的
b=0.8#b也一样
y=np.sum(w*x)+b
if y<=0:
return 0
else:
return 1
def AND(x1,x2):
x=np.array([x1,x2])
w=np.array([0.6,0.6])#w是可变的
b=-0.8#b也一样
#w=[0.5,0.5],b=-0.7也可
y=np.sum(w*x)+b
if y<=0:
return 0
else:
return 1
def XOR(x1,x2):
return AND(NAND(x1,x2),OR(x1,x2))
print(XOR(0,0))
print(XOR(0,1))
print(XOR(1,0))
print(XOR(1,1))

图示如下,可以看到是一个有向无环图,其中 x 1 , x 2 x_1,x_2 x1,x2与 s 1 , s 2 s_1,s_2 s1,s2是全连接,整个图有点像网络流。
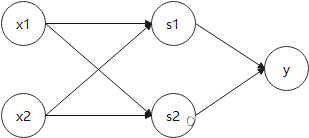
总结
在数字电路和基本的线性规划基础上,理解感知机是不难的,感知机作为深度学习的起点和敲门砖,实在是一个非常巧妙的结构,此书也讲解的非常透彻、便于理解。
参考文献
- 《深度学习入门——基于Python的理论与实践》