LeetCode-460. LFU 缓存【设计 哈希表 链表 双向链表】
- 题目描述:
- 解题思路一:一张图秒懂 LFU!
- 解题思路二:精简版!两个哈希表,一个记录所有节点,一个记录次数链表【defaultdict(new_list),只是记录虚拟节点,会自动创建】。双链表实现多了一个freq,同时维护一个min_freq,每次删除节点的时候都要维护记录次数链表和min_freq。注意当节点超出容量的时候在self.freq_to_dummy[self.min_freq]里面删除尾部节点。
- 解题思路三:0
题目描述:
请你为 最不经常使用(LFU)缓存算法设计并实现数据结构。
实现 LFUCache 类:
LFUCache(int capacity) - 用数据结构的容量 capacity 初始化对象
int get(int key) - 如果键 key 存在于缓存中,则获取键的值,否则返回 -1 。
void put(int key, int value) - 如果键 key 已存在,则变更其值;如果键不存在,请插入键值对。当缓存达到其容量 capacity 时,则应该在插入新项之前,移除最不经常使用的项。在此问题中,当存在平局(即两个或更多个键具有相同使用频率)时,应该去除 最久未使用 的键。
为了确定最不常使用的键,可以为缓存中的每个键维护一个 使用计数器 。使用计数最小的键是最久未使用的键。
当一个键首次插入到缓存中时,它的使用计数器被设置为 1 (由于 put 操作)。对缓存中的键执行 get 或 put 操作,使用计数器的值将会递增。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
示例:
输入:
[“LFUCache”, “put”, “put”, “get”, “put”, “get”, “get”, “put”, “get”, “get”, “get”]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [3], [4, 4], [1], [3], [4]]
输出:
[null, null, null, 1, null, -1, 3, null, -1, 3, 4]
解释:
// cnt(x) = 键 x 的使用计数
// cache=[] 将显示最后一次使用的顺序(最左边的元素是最近的)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=[1,_], cnt(1)=1
lfu.put(2, 2); // cache=[2,1], cnt(2)=1, cnt(1)=1
lfu.get(1); // 返回 1
// cache=[1,2], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 去除键 2 ,因为 cnt(2)=1 ,使用计数最小
// cache=[3,1], cnt(3)=1, cnt(1)=2
lfu.get(2); // 返回 -1(未找到)
lfu.get(3); // 返回 3
// cache=[3,1], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // 去除键 1 ,1 和 3 的 cnt 相同,但 1 最久未使用
// cache=[4,3], cnt(4)=1, cnt(3)=2
lfu.get(1); // 返回 -1(未找到)
lfu.get(3); // 返回 3
// cache=[3,4], cnt(4)=1, cnt(3)=3
lfu.get(4); // 返回 4
// cache=[3,4], cnt(4)=2, cnt(3)=3
提示:
1 <= capacity <= 104
0 <= key <= 105
0 <= value <= 109
最多调用 2 * 105 次 get 和 put 方法
LeetCode-146. LRU 缓存【设计 哈希表 链表 双向链表】, 这两题是十分相似的。!
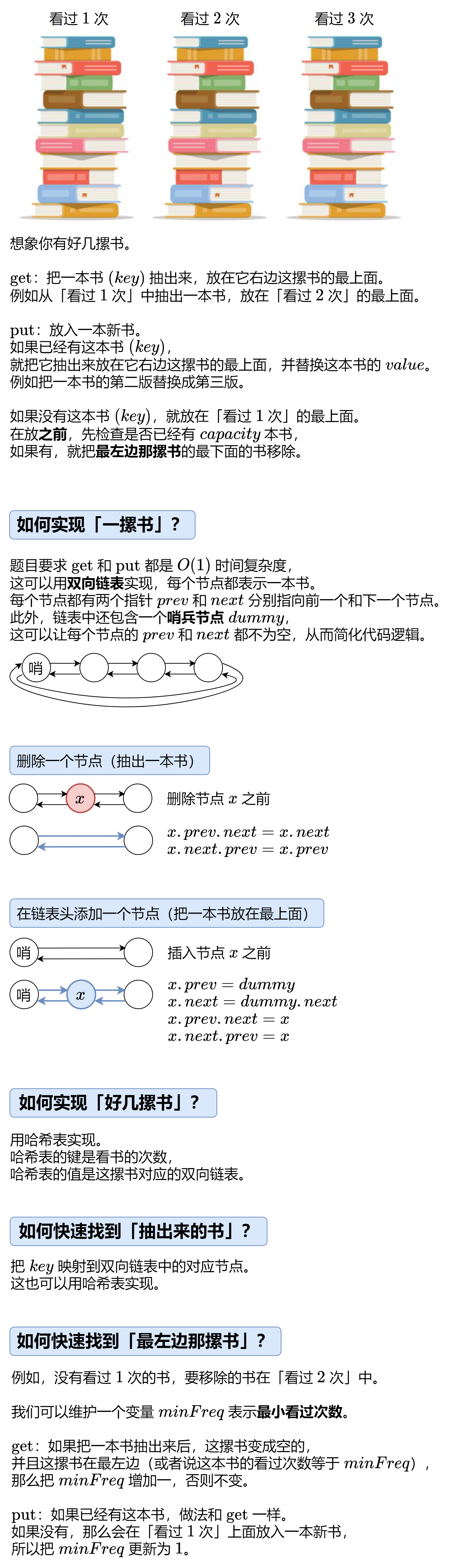
解题思路一:一张图秒懂 LFU!
class Node:
# 提高访问属性的速度,并节省内存
__slots__ = 'prev', 'next', 'key', 'value', 'freq'
def __init__(self, key=0, val=0):
self.key = key
self.value = val
self.freq = 1 # 新书只读了一次
class LFUCache:
def __init__(self, capacity: int):
self.capacity = capacity
self.key_to_node = dict()
def new_list() -> Node:
dummy = Node() # 哨兵节点
dummy.prev = dummy
dummy.next = dummy
return dummy
self.freq_to_dummy = defaultdict(new_list)
def get_node(self, key: int) -> Optional[Node]:
if key not in self.key_to_node: # 没有这本书
return None
node = self.key_to_node[key] # 有这本书
self.remove(node) # 把这本书抽出来
dummy = self.freq_to_dummy[node.freq]
if dummy.prev == dummy: # 抽出来后,这摞书是空的
del self.freq_to_dummy[node.freq] # 移除空链表
if self.min_freq == node.freq: # 这摞书是最左边的
self.min_freq += 1
node.freq += 1 # 看书次数 +1
self.push_front(self.freq_to_dummy[node.freq], node) # 放在右边这摞书的最上面
return node
def get(self, key: int) -> int:
node = self.get_node(key)
return node.value if node else -1
def put(self, key: int, value: int) -> None:
node = self.get_node(key)
if node: # 有这本书
node.value = value # 更新 value
return
if len(self.key_to_node) == self.capacity: # 书太多了
dummy = self.freq_to_dummy[self.min_freq]
back_node = dummy.prev # 最左边那摞书的最下面的书
del self.key_to_node[back_node.key]
self.remove(back_node) # 移除
if dummy.prev == dummy: # 这摞书是空的
del self.freq_to_dummy[self.min_freq] # 移除空链表
self.key_to_node[key] = node = Node(key, value) # 新书
self.push_front(self.freq_to_dummy[1], node) # 放在「看过 1 次」的最上面
self.min_freq = 1
# 删除一个节点(抽出一本书)
def remove(self, x: Node) -> None:
x.prev.next = x.next
x.next.prev = x.prev
# 在链表头添加一个节点(把一本书放在最上面)
def push_front(self, dummy: Node, x: Node) -> None:
x.prev = dummy
x.next = dummy.next
x.prev.next = x
x.next.prev = x
时间复杂度:O(1)
空间复杂度:O(min(p,capacity)),其中 p 为 put 的调用次数。
解题思路二:精简版!两个哈希表,一个记录所有节点,一个记录次数链表【defaultdict(new_list),只是记录虚拟节点,会自动创建】。双链表实现多了一个freq,同时维护一个min_freq,每次删除节点的时候都要维护记录次数链表和min_freq。注意当节点超出容量的时候在self.freq_to_dummy[self.min_freq]里面删除尾部节点。
from collections import defaultdict
class DLinkNode:
def __init__(self, key = 0, value = 0):
self.key = key
self.value = value
self.prev = None
self.next = None
self.freq = 1
class LFUCache:
def __init__(self, capacity: int):
self.capacity = capacity
self.key_to_node = dict()
def new_DLinkList():
dummy = DLinkNode()
dummy.next = dummy
dummy.prev = dummy
return dummy
self.freq_to_dummy = defaultdict(new_DLinkList)
def get_node(self, key):
if key not in self.key_to_node:
return None
node = self.key_to_node[key]
self.remove(node)
dummy = self.freq_to_dummy[node.freq]
if dummy.prev == dummy:
del self.freq_to_dummy[node.freq]
if self.min_freq == node.freq:
self.min_freq += 1
node.freq += 1
self.push_front(self.freq_to_dummy[node.freq], node)
return node
def get(self, key: int) -> int:
node = self.get_node(key)
return node.value if node else -1
def put(self, key: int, value: int) -> None:
node = self.get_node(key)
if node:
node.value = value
return
node = DLinkNode(key, value) # 一定是新的,要在插入前空出位置
if len(self.key_to_node) == self.capacity:
dummy = self.freq_to_dummy[self.min_freq]
tail = dummy.prev
del self.key_to_node[tail.key]
self.remove(tail)
if dummy.prev == dummy:
del self.freq_to_dummy[tail.freq]
self.key_to_node[key] = node
self.push_front(self.freq_to_dummy[1], node)
self.min_freq = 1
def remove(self, x):
x.next.prev = x.prev
x.prev.next = x.next
def push_front(self, dummy, x):
x.next = dummy.next
x.prev = dummy
x.prev.next = x
x.next.prev = x
# Your LFUCache object will be instantiated and called as such:
# obj = LFUCache(capacity)
# param_1 = obj.get(key)
# obj.put(key,value)
时间复杂度:O(1)
空间复杂度:O(min(p,capacity)),其中 p 为 put 的调用次数。
解题思路三:0
时间复杂度:O(1)
空间复杂度:O(min(p,capacity)),其中 p 为 put 的调用次数。



♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠