---

前言

  T_T此专栏用于记录数据结构及算法的（痛苦）学习历程，便于日后复习（这种事情不要啊）。所用教材为《数据结构 C语言版 第2版》严蔚敏。

---

一、二叉树的定理

  在树和二叉树的定义和基本术语中介绍了二叉树的定义和基本术语。二叉树具有多种定理。
  性质1：在二叉树的第 i 层上至多有 2^( i - 1) (i>=1)个结点。
  性质2：深度为 k 的二叉树至多有 2^k - 1 个结点 (k>=1)。
  性质3：对任何一棵二叉树T, 如果其终端结点(即叶子结点)数为n0，度为2的结点数为n2，则 n0 = n2 + 1。

二、满二叉树与完全二叉树

1.满二叉树的定义

  满二叉树是一种特殊的二叉树：深度为 k 且含有 2^ k - 1个结点的二叉树。其特点是：每一层上的结点数都是最大结点数，即每一层 i 的结点数都具有最大值 2^( i - 1)。

  对满二叉树的结点进行连续编号，约定编号从根结点起，自上而下，自左至右。由此可引出完全二叉树的定义。

2.完全二叉树的定义

  完全二叉树的定义：深度为 k 的，有 n 个结点的二叉树，当且仅当其每一个结点都与深度为 k 的满二叉树中编号从 1 至 n 的结点一一对应时， 称之为完全二叉树。（看不懂？简单来说就是完全二叉树每个结点的编号在结点对应位置上是连续的！）
  完全二叉树的特点是：
  (1)叶子结点只可能在层次最大的两层上出现。例如深度为 i 的完全二叉树，其叶子结点只能出现在第 i - 1 层和第 i 层。
  (2)对任一结点，若其右分支下的子孙的最大层次为 l ，则其左分支下的子孙的最大层次必为 l 或 l + 1。（由此才能满足完全二叉树的定义）

3.完全二叉树的特殊定理

  性质 4：具有 n 个结点的完全二叉树的深度为 [ lb n ] +1（lb表示以2为底的log）向下取整（即取不大于 lb n 的最大整数再加1）。
  性质 5：如果对一棵有 n 个结点的完全二叉树的结点按层序编号（从上到下， 从左到右）， 则对任一结点 i (1<=i<=n), 有:
  (1)如果 i = 1, 则结点 i 是二叉树的根，无双亲；如果 i > 1, 则其双亲是结点 [ i / 2 ](不大于 i / 2 的最大整数)。
  (2)如果 2i > n, 则结点 i 无左孩子（结点 i 为叶子结点）；否则其左孩子是结点 2i。
  (3)如果 2i+1 > n, 则结点 i 无右孩子；否则其右孩子是结点 2i+1。

三、完全二叉树的存储结构

  与线性表类似，二叉树也有顺序存储和链式存储两种方式。

1.顺序存储结构

  顺序存储结构使用一组地址连续的存储单元来存储数据元素，为了能够在存储结构中反映出结点之间的逻辑关系，必须将二叉树以完全二叉树的形式保存，即结点依照完全二叉树的定义按序号存储。

//-----二叉树的顺序存储表示－－－－－
#define MAXTSIZE 100 
typedef TElemType SqBiTree [MAXTSIZE];   //二叉树的最大结点数
SqBiTree bt;							 //0号单元存储根结点

  对于一般二叉树转化为完全二叉树后空缺的位置，以填充NULL来代替。

  由此可见，这种顺序存储结构仅适用于完全二叉树。因为，在最坏的情况下，一个深度为K且只有K个结点的单支树（只有左子树或只有右子树，树中不存在度为2的结点），却需要长度为 2^k - 1的一维数组，造成存储空间极大浪费。

2.链式存储结构

  二叉树的结点由一个数据元素和分别指向其左、 右子树的两个分支构成，则表示二叉树的链表中的结点至少包含 3 个域：数据域和左、 右指针域。对于子树不存在的情况，则该指针为空。
  下图所示为二叉链表和三叉链表（额外增加一个指针指向其双亲）的形式。

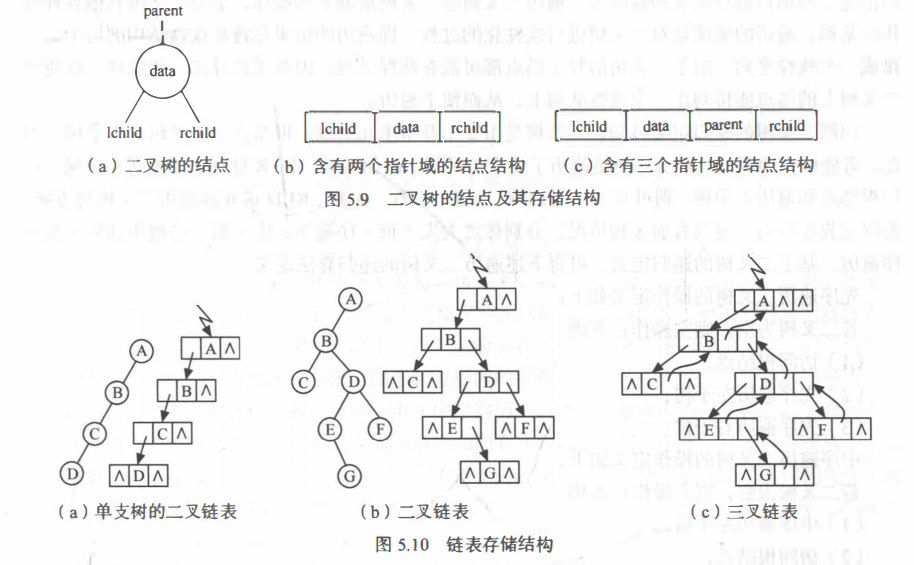
  采用二叉链表还是三叉链表，应根据实际应用进行选取。下面为二叉链表的存储表示。

//- - - - -二叉树的二叉链表存储表示－ －－－－
typedef struct BiTNode{ 
TElemType data;      			//结点数据域
struct BiTNode *lchild,*rchild; //左右孩子指针
) BiTNode,*BiTree;

---

总结

  路漫漫其修远兮，吾将上下而摆烂。（又是划水的一天，water,water,water,water,water…）
  有任何疑问和补充，欢迎交流。（但我显然不会T_T）