问题描述:
有一个N*N的棋盘,需要将N个皇后放在棋盘上,保证棋盘的每一行每一列每一左斜列每一右斜列都最多只能有一个皇后。
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
像下图这样的放置即满足条件:
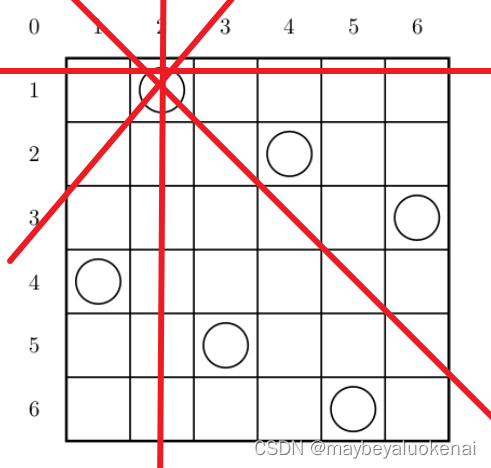
这是一组答案的样式:

思路解析:
可以很明显的看到,这是一个对列进行排列型枚举问题。如果我们暴力搜索每一种列排列,再对其验证是否满足条件,当有6个皇后就有6!==720种方案,时间复杂度很高O(n!*n)。
很显然暴力枚举是不切实际的做法,有时候我们放置i个皇后(i<n)发现冲突时就已经不满足条件了,这部分可以进行剪枝。
总体思路:
使用回溯的思想,依次在1-n行放入皇后,保证放入第i行的皇后不会和前i-1个皇后发生冲突,当我们放到第n+1个时此时n个皇后已经放置完毕,并且保证前n个不冲突即找到答案。
当放到第i行时(i<=n)发现不管放在该行的哪一列都会产生冲突时,此时说明当前方案不合适,回溯到i-1行重新选择皇后进行放置。
关于如何判断是否产生冲突,使用状态码表示哪些行哪些列哪些斜列可以放置,每放置一个皇后将它能攻击的范围给他置为0。
关于状态压缩:使用二进制的表示方式,0代表该行/列/斜列不能放置了,1则可以放置
直接给出详细代码及其解析好吧!!!
代码及注释详解:
#include<iostream>
#include<unordered_map>
using namespace std;
int arr[15];
//掩码到实际列的映射
unordered_map<int, int>umap;
int k = 3;
void print_one_result(int n) {
if (k) {
for (int i = 1; i <= n; i++) {
if (i != 1)cout << " " << arr[i];
else cout << arr[i];
}
cout << endl;
k--;
}
}
//a 枚举到第几行
//b 哪些列可以选
//c 哪些做些列可以选
//d 哪些右斜列可以选
//e 几个皇后
int dfs(int a, int b, int c, int d, int e) {
//所有皇后放置完毕
if (a > e) {
print_one_result(e);
return 1;
}
int ans = 0;
//j代表第几列
for (int t = b, j; t; t -= t & (-t)) {
j = umap[t & (-t)];
arr[a] = j;
//说明该放置位置(a,j)不产生冲突
if ((c & (1 << a + j - 1)) && (d & (1 << a - j + e))) {
//递归到下一行放置
//并且禁用该范围
ans += dfs(a + 1, b ^ (t & -t), c ^ (1 << a + j - 1), d ^ (1 << a - j + e), e);
}
}
return ans;
}
void Nqueen() {
int n;
cin >> n;
//掩码到实际表示的映射 :比如 0100表示第2(行/列/斜列)
for (int i = 1; i <= n; i++) {
umap[1 << i] = i;
}
//刚开始每一列都没有放置 假设n==6
//(1 << (n + 1)) - 2 代表 01111110 有6列可以放置
//0111111111110 代表斜列
cout << dfs(1, (1 << (n + 1)) - 2, (1 << n * 2) - 2, (1 << n * 2) - 2, n);
}
int main() {
Nqueen();
return 0;
}