第一次更新:2024/5/7
目录
一. 引入
基础概念
二. 测角原理
1. 接收天线不同位置
2. 角度几何关系
3. 角度正负规定
4. 角度测量
5. 最大不模糊角
三. 角度分辨率
1. 相位变化量
2. 角度表示
3. 角度变化量
三. 测角算法
1. 三维快速傅里叶变换 (3D-FFT:Three-Dimensional Fast Fourier Transform)
1) 原理
2) matlab代码
2. 波束形成技术(DBF:Digital Beam Forming)
1)原理
2)波束形成算法(matlab代码)
3. 多元信号分类算法(MUSIC:Multiple Signal Classification)
1)原理
2)MUSIC算法(matlab代码)
一. 引入
毫米波雷达测角测得是哪个角呢?
传统的毫米波雷达角度测量是特指水平面方位角的测量,即目标物体相对于雷达“正方向”的偏离角度(正方向也就是垂直于雷达天线板的法线方向),如下图:
基础概念
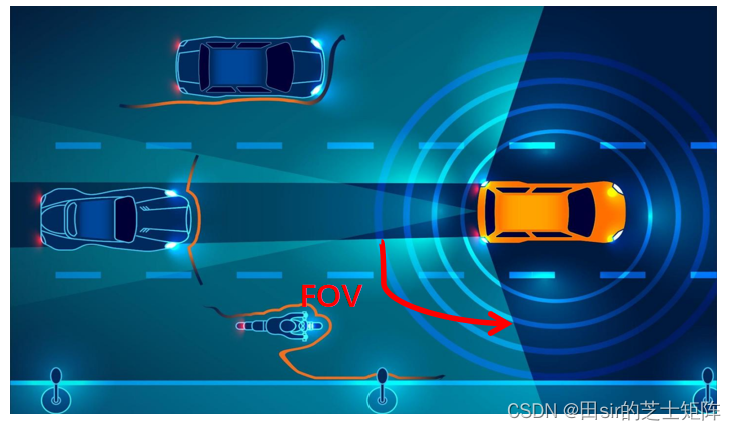
- 到达角(AOA:Angle of Arrival): 指接收机中的天线阵列或单个天线接收到雷达信号时,根据信号相位差或时间差计算出来的信号到达方向。
- 雷达的视场(FOV:Field of View): 顾名思义为雷达的“视野范围”,可以理解为AOA的值域。如图所示为前向毫米波雷达以及角雷达的FOV。
二. 测角原理
毫米波雷达方位角的测量主要依赖于接收天线(RX),角度测量的基本原理即通过回波信号在接收天线的距离差d来估计相位差∆∅。
1. 接收天线不同位置
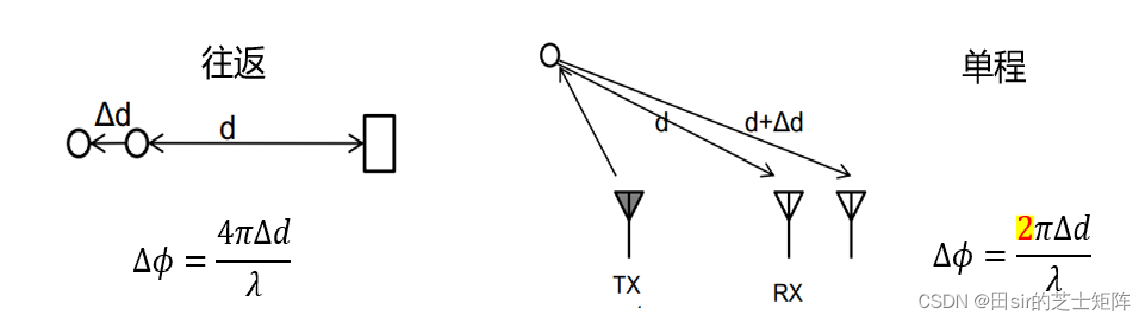
假设电磁波的发出与接收天线为同一根:
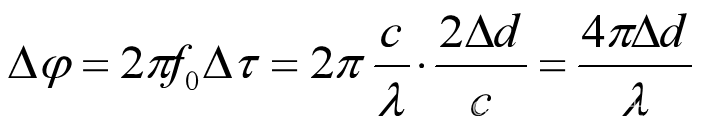
假设电磁波的发射与接收天线不同,则在接收天线处的相位差为:
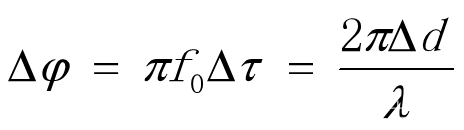
其中,为初始发波频率,Δd为相邻接收天线的距离差,Δτ为时间差,λ为波长。
2. 角度几何关系

根据距离差Δd与角度θ的几何关系:
![]()
3. 角度正负规定
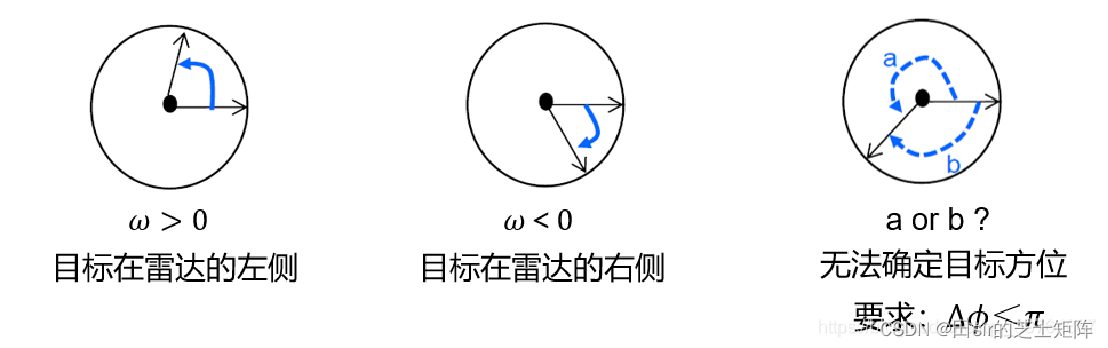
4. 角度测量

可以进行障碍物的角度估计,得到测角公式:
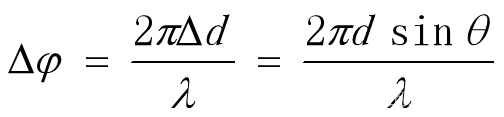
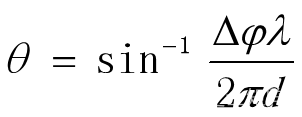
由测角公式可得:相位差是关于角度的非线性函数。
- 当角度θ越接近0°时,角度估算精度越高;
- 当角度θ越接近90°时,角度估算精度越低。
5. 最大不模糊角
当角度范围超过180°时,会造成测量角度不准确,即有“最大不模糊角”:
故此时最大到达角(AOA: Angle of Arrival)为:

从理论角度来看,最大视场角(FOV:Field of View)为:
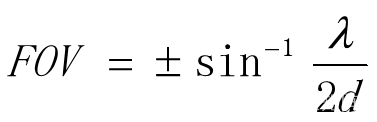
三. 角度分辨率
角度分辨率(θres )是两个物体在角度 FFT 中可显示为两个谱峰时的最小角度间隔。
1. 相位变化量

2. 角度表示
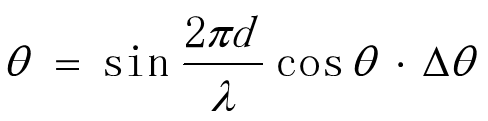
又因为:

所以:
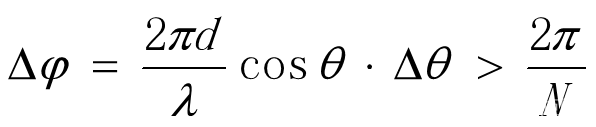
3. 角度变化量


三. 测角算法
最常见的角度测量方式为:3D-FFT(三维快速傅里叶变换),DBF(数字波束形成技术)以及MUSIC算法。其中,3D-FFT(三维快速傅里叶变换)和DBF(数字波束形成技术)做DOA估计是最简单且运算复杂度最低的方法,但是这两方法并不能实现超分辨,其角分辨率受限于阵列的孔径,MUSIC算法是实现超分辨的一种算法。
超分辨:据已知图像信息恢复图像细节和其他数据信息的过程,简单来说就是增大图像的分辨率,防止其图像质量下降。(也就是让图像更加清晰的能力)
1. 三维快速傅里叶变换 (3D-FFT:Three-Dimensional Fast Fourier Transform)
1) 原理

在进行完慢时间维FFT和快时间维FFT后,在2D-FFT峰值相对应的相位序列进行FFT,图中雷达对两个目标进行探测。FFT的点数为天线的阵列数N,FFT后得到两个目标对应的相位变化量,
。
根据角度估算公式:
即可得到障碍物的角度为:
2) 3D-FFT(matlab代码)
% generate signal and array response
fs = 100e3; % sample rate
f0 = 20e3; % signal frequency
t = 0:1/fs:0.1; % time vector
s = sin(2*pi*f0*t); % signal
d = 0.02; % element spacing
N = 8; % number of elements
theta = 10; % target angle
c = 343; % speed of sound
lambda = c/f0; % wavelength
k = 2*pi/lambda; % wavenumber
d_array = d*(0:N-1); % array element positions
phi_array = exp(-1i*k*d_array*cosd(theta)); % array response
x = s*phi_array; % received signal
X = fftshift(fft2(x)); % 2D FFT
[m, n] = size(X); % size of FFT matrix
theta_x = asind((-m/2:m/2-1)/(m/2)*sin(pi/2)); % angle axis
theta_y = asind((-n/2:n/2-1)/(n/2)*sin(pi/2)); % angle axis
[X_max, I] = max(abs(X(:))); % find max value in FFT matrix
[I_row, I_col] = ind2sub([m n],I); % find row and column index
theta_x(I_row) % estimate angle in x direction
theta_y(I_col) % estimate angle in y direction2. 波束形成技术(DBF:Digital Beam Forming)
1)原理
DBF本质是构造视场范围内的各个角度的导向矢量,并用这些导向矢量分别去和阵列的回波信号相乘以得到各个角度下的能量值,我们通过寻找其中的极大值(目标所处方向的回波与导向矢量相干叠加,这些方向的能量会得到增强,而噪声是非相干的,能量得到增强的方向,对应极大值的位置,也即信号的方向)来得到实际回波的方向而达到测角的目的。
信号模型:
假设在平面上均匀排布着M-1个阵列(也就是天线)
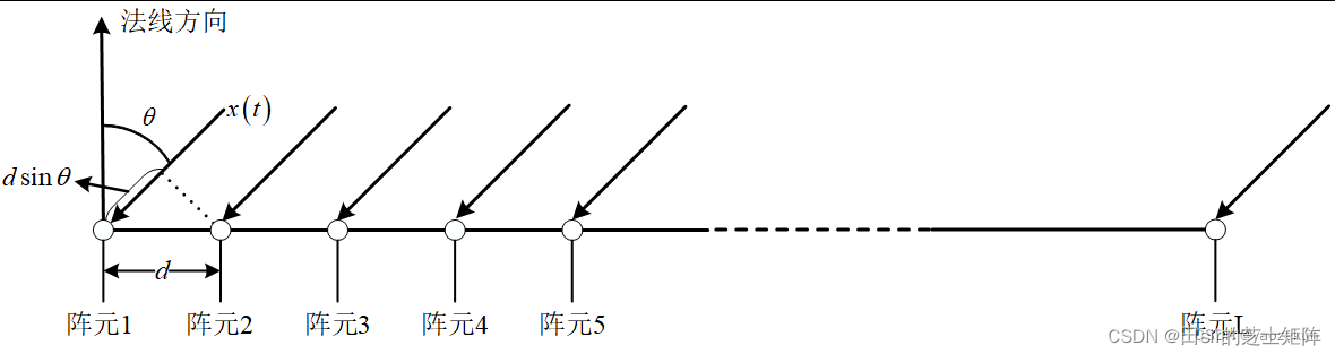
设窄带发射信号为:s(t),则阵列接收到的信号x(t)为:
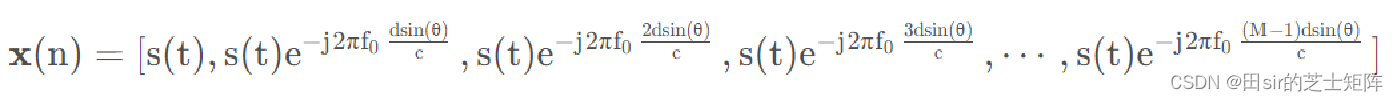
定义导向矢量为:

故:
x(n)=a(θ)s(t)
导向矢量是阵列天线的所有阵元对具有单位能量窄带信源的响应。由于阵列响应在不同方向上是不同的,导向矢量与信源的方向是相互关联的,这种关联的独特性依赖于阵列的几何结构。对于同一阵元阵列,导向矢量的每一个元素具有单位幅度。
总输出为:
令导矢向量中的角度θ在[0,π]中遍历,使得总输出y(t)的模值最小,此时满足条件的角度即波束形成技术所求得的DOA估计角度。
2)波束形成算法(matlab代码)
数字波束合成可以等效的理解为让发射波束按照指定方向来发射电磁波
实际操作过程中的数字波束是通过回波信号FFT之后的峰值点在通过一个阵列流来改变波束的指向来实现的
波束形成技术中常用两种算法:
- LCMV算法:在有用信号形式以及信号方向完全已知的情况下,在某种约束条件下,使得阵列的输出的方差最小。
LCMV仿真图:
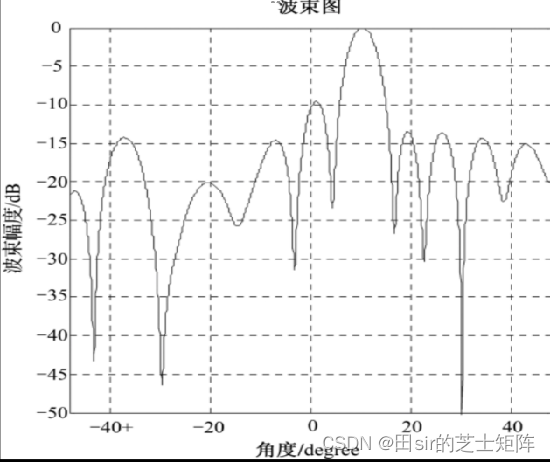
- LMS算法:采用迭代模式,为每个步骤迭代n时刻的权向量加上一个校正值后,即可组成m+1时刻的权向量,用它逼近最优权向量。
LMS仿真图:
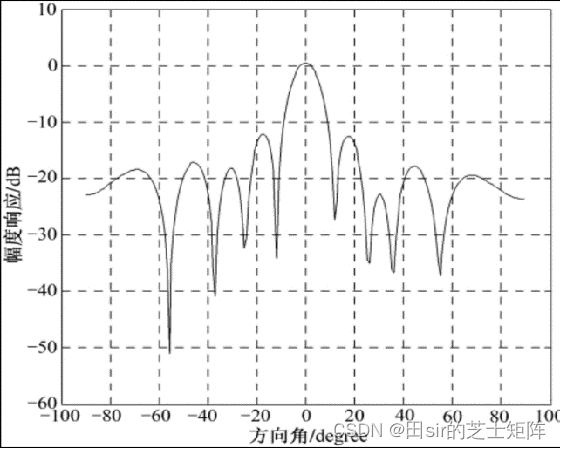
% 生成一个6个天线的阵列
N = 6;
theta = linspace(-pi/2, pi/2, 181);
d = 0.5;
array = phased.ULA(N, d);
% 生成两个目标
pos = [-20 5; 10 -10];
fc = 3e8/77e9;
lambda = fc/2;
c = 3e8;
t = (0:0.1e-6:1000e-6)';
s1 = cos(2*pi*fc*t + 2*pi*pos(1,1)*sin(pos(1,2)*pi/180)/c);
s2 = cos(2*pi*fc*t + 2*pi*pos(2,1)*sin(pos(2,2)*pi/180)/c);
s = s1 + s2;
% 接收到的信号
rx = array(s, [0;5;10;15;20;25]*1e-3);
% DBF估计到达角
angdbf = phased.PhaseShiftBeamformer('SensorArray', array, 'OperatingFrequency', fc, ...
'Direction', [-90:90], 'PropagationSpeed', c);
[y,doasdbf] = angdbf(rx);
doasdbf = unwrap(doasdbf)*180/pi;
disp(doasdbf);
% define parameters
fs = 100e3; % sample rate
f0 = 20e3; % signal frequency
t = 0:1/fs:0.1; % time vector
s = sin(2pif0t); % signal
d = 0.02; % element spacing
N = 8; % number of elements
theta = 10; % target angle
c = 343; % speed of sound
lambda = c/f0; % wavelength
k = 2pi/lambda; % wavenumber
d_array = d*(0:N-1); % array element positions
phi_array = exp(-1ikd_arraycosd(theta)); % array response
x = sphi_array; % received signal
% DBF processing
theta_range = -90:1:90; % angle range
w = ones(1,N); % weighting coefficients
P = zeros(size(theta_range)); % power spectrum
for i = 1:length(theta_range)
phi = exp(-1ikd_array'sind(theta_range(i))); % steering vector
y = wx.phi; % beamformed signal
P(i) = abs(sum(y))^2/(Nsum(abs(y).^2)); % power spectrum
end
% find peak angle
[P_max, I] = max(P);
theta_est = theta_range(I);
% plot results
figure;
plot(theta_range, P);
hold on;
plot(theta_est, P_max, 'r*');
xlabel('Angle (degree)');
ylabel('Power spectrum');
title('DBF');
legend('Power spectrum', 'Estimated angle');3. 多元信号分类算法(MUSIC:Multiple Signal Classification)
MUSIC(Multiple Signal Classification),多重信号分类,是一类空间谱估计算法。其思想是利用接收数据的协方差矩阵进行特征分解,分离出信号子空间和噪声子空间,利用信号导矢向量与噪声子空间的正交性来构成空间扫描谱,进行全域搜索谱峰,从而实现信号的参数估计。
1)原理
假设N元等距线阵,阵元间距为d,信号的波长为λ,空间中有r个信源,那么接收到的观测信号可表示为:
其中为第i个信号,
为第i个信号的入射角度,
为导矢向量,N(t)为高斯白噪声。
其协方差矩阵为:
将一组完备的正交基分为信号子空间和噪声子空间:
又因为:
代入得:
即表明信号来波方向的相位矢量A与噪声特征值对应 的特征向量正交
定义一个噪声矩阵:
根据上式可以得到:
构造空间谱:
其中,
遍历空间搜索角度,当搜索到角度θ的时候,此时
有一尖峰,对应角度即障碍物角度。
2)MUSIC算法(matlab代码)
MUSIC仿真图:
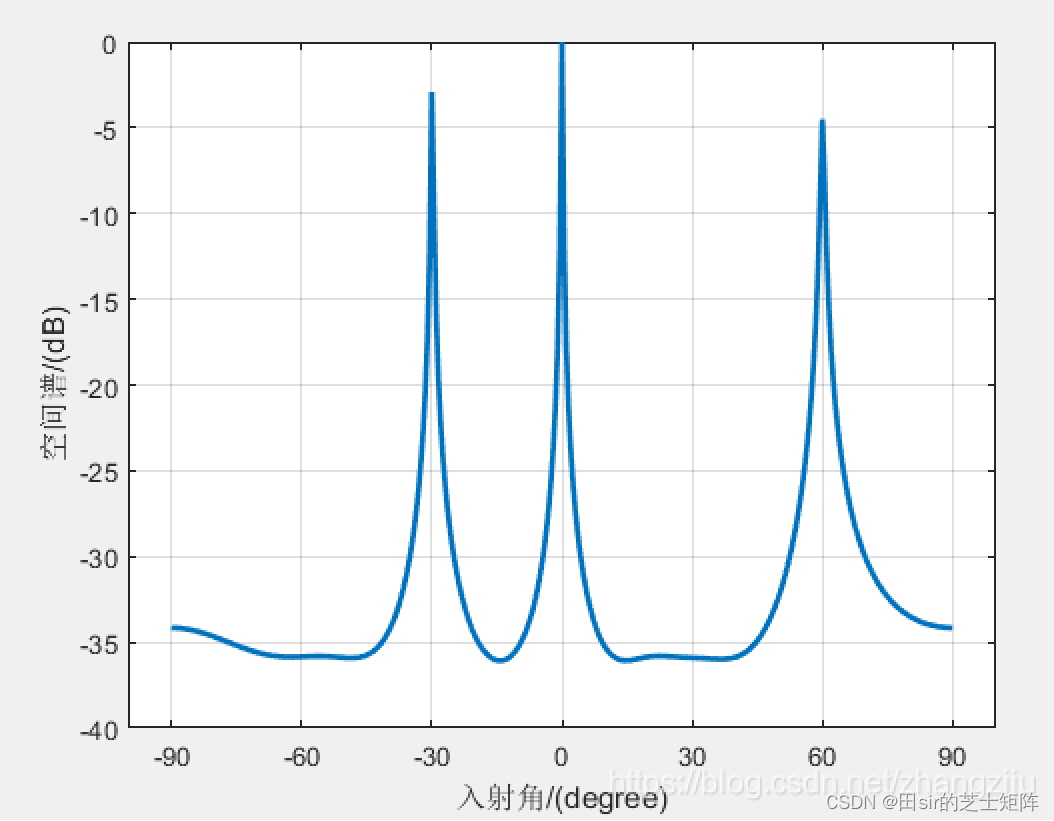
代码:
% 生成一个6个天线的阵列
N = 6;
theta = linspace(-pi/2, pi/2, 181);
d = 0.5;
array = phased.ULA(N, d);
% 生成两个目标
pos = [-20 5; 10 -10];
fc = 3e8/77e9;
lambda = fc/2;
c = 3e8;
t = (0:0.1e-6:1000e-6)';
s1 = cos(2*pi*fc*t + 2*pi*pos(1,1)*sin(pos(1,2)*pi/180)/c);
s2 = cos(2*pi*fc*t + 2*pi*pos(2,1)*sin(pos(2,2)*pi/180)/c);
s = s1 + s2;
% 接收到的信号
rx = array(s, [0;5;10;15;20;25]*1e-3);
% MUSIC估计到达角
angmusic = phased.MUSIC('SensorArray', array, 'OperatingFrequency', fc, 'NumSignals', 2, 'ScanAngles', theta);
[Pmusic,doasmusic] = step(angmusic, rx);
doasmusic = unwrap(doasmusic)*180/pi;
disp(doasmusic);
% generate signal and array response
fs = 100e3; % sample rate
f0 = 20e3; % signal frequency
t = 0:1/fs:0.1; % time vector
s = sin(2*pi*f0*t); % signal
d = 0.02; % element spacing
N = 8; % number of elements
theta = [10, 20]; % target angles
c = 343; % speed of sound
lambda = c/f0; % wavelength
k = 2*pi/lambda; % wavenumber
d_array = d*(0:N-1); % array element positions
phi_array = exp(-1i*k*d_array'*cosd(theta)); % array response
x = s*phi_array; % received signal
% MUSIC processing
theta_range = -90:1:90; % angle range
U = svd(x); % singular values of received signal
n = length(U); % number of eigenvalues
P = zeros(size(theta_range)); % power spectrum
for i = 1:length(theta_range)
phi = exp(-1i*k*d_array'*cosd(theta_range(i))); % steering vector
En = eye(n)-U*U'; % noise subspace projection matrix
P(i) = 1/abs(phi'*En*En'*phi); % power spectrum
end
% find peak angles
[P_max, I] = sort(P, 'descend');
theta_est = theta_range(I(1:2));
% plot results
figure;
plot(theta_range, P);
hold on;
plot(theta_est, P_max(1:2), 'r*');
xlabel('Angle (degree)');
ylabel('Power spectrum');
title('MUSIC');
legend('Power spectrum', 'Estimated angles');参考:
详细介绍雷达到达角估计算法3DFFT,DBF,MUSIC,Capon的原理、对比、各自的优势_雷达dbf技术-CSDN博客
《深入浅出通信原理》陈爱军
《阵列信号处理及MATLAB实现》张小飞