MIT加州理工等革命性KAN破记录，发现数学定理碾压DeepMind！KAN论文解读

KAN的数学原理

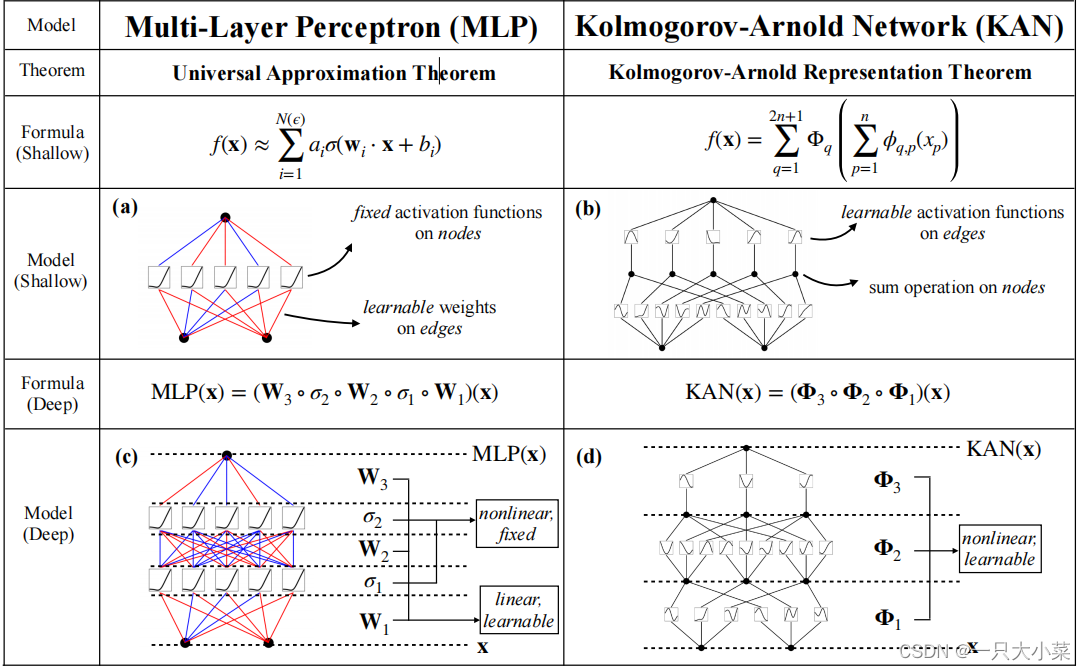
如果f是有界域上的多元连续函数，那么f可以被写成关于单个变量和加法二元操作的连续函数的有限组合。更具体地说，对于光滑函数f：[0, 1]ⁿ → R，有
$f(x_1, \ldots , x_n) = \sum_{q=1}^{2n+1} \Phi_q \sum_{p=1}^n \phi_{q,p}(x_p)$

其中从某种意义上说，他们证明了 $\phi_{q,p} : [0, 1] → R \text{ 且 } \Phi_q : R → R$ 唯一真正的多元函数是加法，因为每个其他函数都可以用一元函数和求和来表示。

不必局限于原始的方程式，其中只有两层非线性和隐藏层中的少量项（2n + 1）,我们将将网络泛化为任意宽度和深度。
科学和日常生活中的大多数函数通常是光滑的，并具有稀疏的组合结构，这可能有助于实现平滑的科尔莫戈洛夫-阿诺德表示。

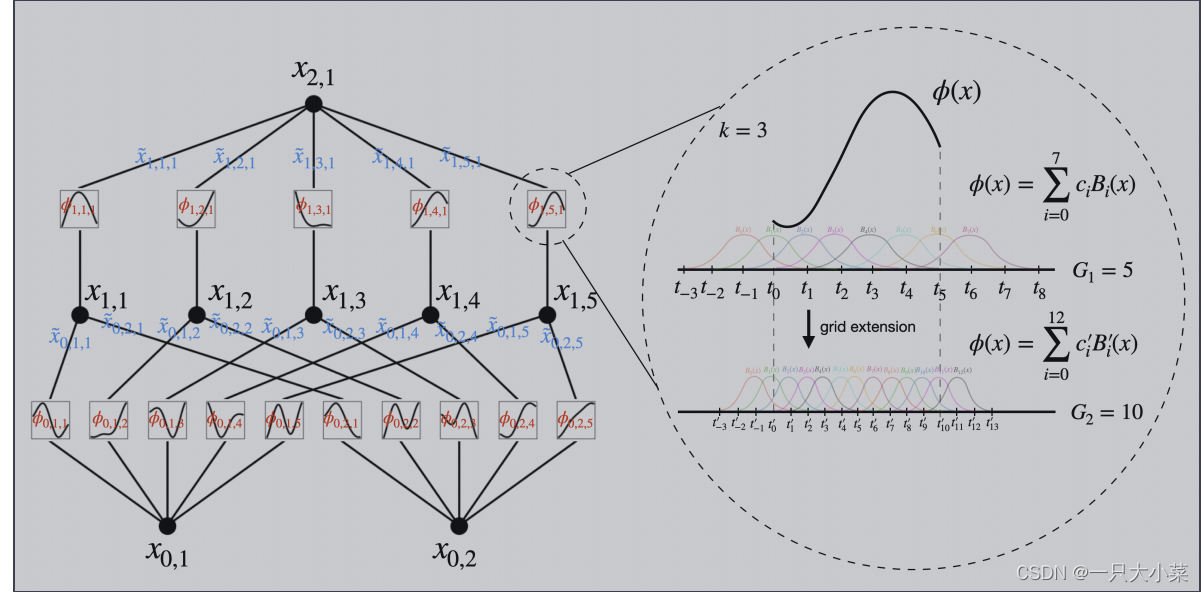
请添加图片描述

KAN的架构

KAN的思想

假设我们有一个监督学习任务，包含输入输出对 {xi, yi}，我们希望找到一个函数 f，使得对于所有数据点，yi ≈ f(xi)。方程暗示了如果我们能找到合适的一元函数 ϕq,p 和 Φq，那么任务就完成了。这启发我们设计了一个神经网络，明确地参数化了方程。由于所有需要学习的函数都是一元函数，我们可以将每个一维函数参数化为一个B样条曲线，其中包括可学习的局部B样条基函数的系数。

符号表示

KAN的形状表示 $[n_0, n_1, \ldots , n_L]$
$n_i$ 是计算图第 $i$ 层中节点的数量。
$(l, i)$ 表示第 $l$ 层中的第 $i$ 个神经元，并用 $x_{l,i}$ 表示 $(l, i)$ 神经元的激活值
在第 $l$ 层和第 $l + 1$ 层之间，有 $n_l n_{l+1}$ 个激活函数：连接 $(l, j)$ 和 $(l + 1, i)$ 的激活函数用 $\phi_{l,i,j}$ 表示，其中 $\ldots , L - 1$ ， $\ldots , n_{l+1}$ ， $\ldots , n_l$ 。

KAN的前向传播

第 (l + 1, j) 个神经元的激活值简单地是所有传入后激活值的总和：
$x_{l+1,j} = \sum_{i=1}^{n_l} \widetilde{x}_{l,i,j} = \sum_{i=1}^{n_l} \phi_{l,i,j} (x_{l,i}), \quad j = 1, \ldots , n_{l+1}.$

矩阵形式
$x_{l+1} = \begin{pmatrix} \phi_{l,1,1}(·) & \phi_{l,1,2}(·) & \cdots & \phi_{l,1,n_l}(·) \\ \phi_{l,2,1}(·) & \phi_{l,2,2}(·) & \cdots & \phi_{l,2,n_l}(·) \\ \vdots & \vdots & \ddots & \vdots \\ \phi_{l,n_{l+1},1}(·) & \phi_{l,n_{l+1},2}(·) & \cdots & \phi_{l,n_{l+1},n_l}(·) \end{pmatrix} x_l,$

一个通用的 KAN 网络是 L 层的组合,则输出
$\text{KAN}(x) = (\Phi_{L-1} \circ \Phi_{L-2} \circ \cdots \circ \Phi_1 \circ \Phi_0)x.$

原始的科尔莫戈洛夫-阿诺德表示方程（2.1）对应于一个形状为[n，2n + 1，1]的2层KAN。所有操作都是可微分的，因此我们可以使用反向传播来训练KAN。

KAN与MLP的比较

请添加图片描述

优化技巧

残差激活函数：在文中公式(2.10)中，每个激活函数 ϕ(x) 被设计为残差形式，即包括一个基函数 𝑏(𝑥) 和一个B-样条函数。这里的 𝑏(𝑥)通常选择为 SiLU 函数，提供了非线性的基本变换，而B-样条部分允许进一步的细粒度调整。这种组合提高了模型对非线性关系的适应性和表达力。
激活函数的尺度初始化：为了确保网络在初始化阶段具有合理的行为，激活函数的部分，特别是B-样条部分，通常初始化为接近零的小值，而权重 𝑤 使用 Xavier 初始化。这种初始化方法帮助避免训练初期的梯度爆炸或消失问题，促进了更稳定的学习过程。
动态更新样条网格：由于B-样条是定义在有限区间的，但激活值可能在训练过程中超出这些区间，因此提出了动态更新网格的方法。这意味着根据激活函数输入的实际分布，调整定义样条函数的网格点，确保模型能够适应输入数据的变化，维持优化性能。

KAN的参数复杂度

我们考虑一个网络：

深度为 L，
每一层的宽度都相等，即 n0 = n1 = · · · = nL = N，
每个样条函数的阶数为 k（通常 k = 3），在 G 个区间上（即 G + 1 个网格点）。

那么总共有大约 O(N^2L(G + k)) ∼ O(N^2LG) 个参数。相比之下，深度为 L，宽度为 N 的MLP只需要大约 O(N^2L) 个参数，这似乎比KAN更为高效。

幸运的是，KAN通常需要的 N 要比MLP小得多，这不仅节省了参数，而且实现了更好的泛化能力（见例如图3.1和3.3），并促进了可解释性。我们将KAN的泛化行为进行了以下的定理刻画。

KAN的逼近能力和缩放定律

逼近理论（KAT）

逼近理论（KAT）：定理2.1（近似理论，KAT）说明了在KAN中使用有限网格大小时，可以用B-样条函数近似函数，并给出了逼近的误差上界。这个误差上界依赖于网格大小，但与函数的维度无关，这意味着KAN在处理高维数据时具有优势，可以避免维度诅咒。

神经网络缩放定律
神经网络的缩放定律描述了测试损失如何随着模型参数数量的增加而减少。这种关系通常表示为 ℓ ∝ N^(-α)，其中 ℓ 是测试的均方根误差（RMSE），N 是模型参数的数量，α 是缩放指数。更大的 α 值意味着通过增加模型规模可以获得更大的性能改进。

Intrinsic dimensionality by Sharma & Kaplan: 此理论提出缩放指数 𝛼 从数据拟合的本征维度 𝑑 派生，缩放律为 ℓ∝𝑁−𝛼，其中 𝛼=(𝑘+1)/𝑑。
Maximum arity by Michaud et al.: 此理论考虑了计算图中最大的分支数（arity），并提出了一个与分支数相关的缩放指数 𝛼=(𝑘+1)/2。
Compositional sparsity by Poggio et al.: 此理论基于组合稀疏性，提出了缩放指数 𝛼=𝑚/2，其中 𝑚 是函数类中导数的阶。
KAN by Liu et al.: KAN 理论则是基于Kolmogorov-Arnold表示，其中提出的缩放指数是 𝛼=𝑘+1。这是因为 KAN 能够分解高维函数为多个一维函数，每个一维函数由样条来近似，从而实现高效的缩放。

在这些理论中，KAN（Kolmogorov-Arnold 网络）提出了一种全新的方法。KAN 将高维函数分解为多个一维函数，并利用光滑的 Kolmogorov-Arnold 表示来近似复杂函数。根据 KAN 的理论，缩放指数 α 取决于样条多项式的分段阶数，与其他工作相比缩放指数更大，拥有更好的拟合效果。

KAT和UAT的比较

通用逼近定理（UAT）：UAT表明，具有足够神经元数量的两层神经网络可以以任意精度近似任何函数。然而，它未提供关于所需神经元数量随误差容限的变化方式的界限，且在高维空间中存在维度诅咒的问题，导致神经元数量可能呈指数增长。
近似理论（KAT）：相比之下，KAT针对KANs（Kolmogorov-Arnold网络）提供了一种更为优化的逼近方法。KAT利用了函数的低维表示，使得神经网络在逼近时更有效率。KANs能够将高维函数分解成多个一维函数，这种分解方式有助于克服维度诅咒，并且使得神经网络更符合符号函数。

综上所述，KAT提供了一种更加灵活和高效的逼近方法，相比之下，UAT在高维空间中的逼近效果可能会受到限制，并且可能需要大量的神经元来达到所需的精度。

网格扩展

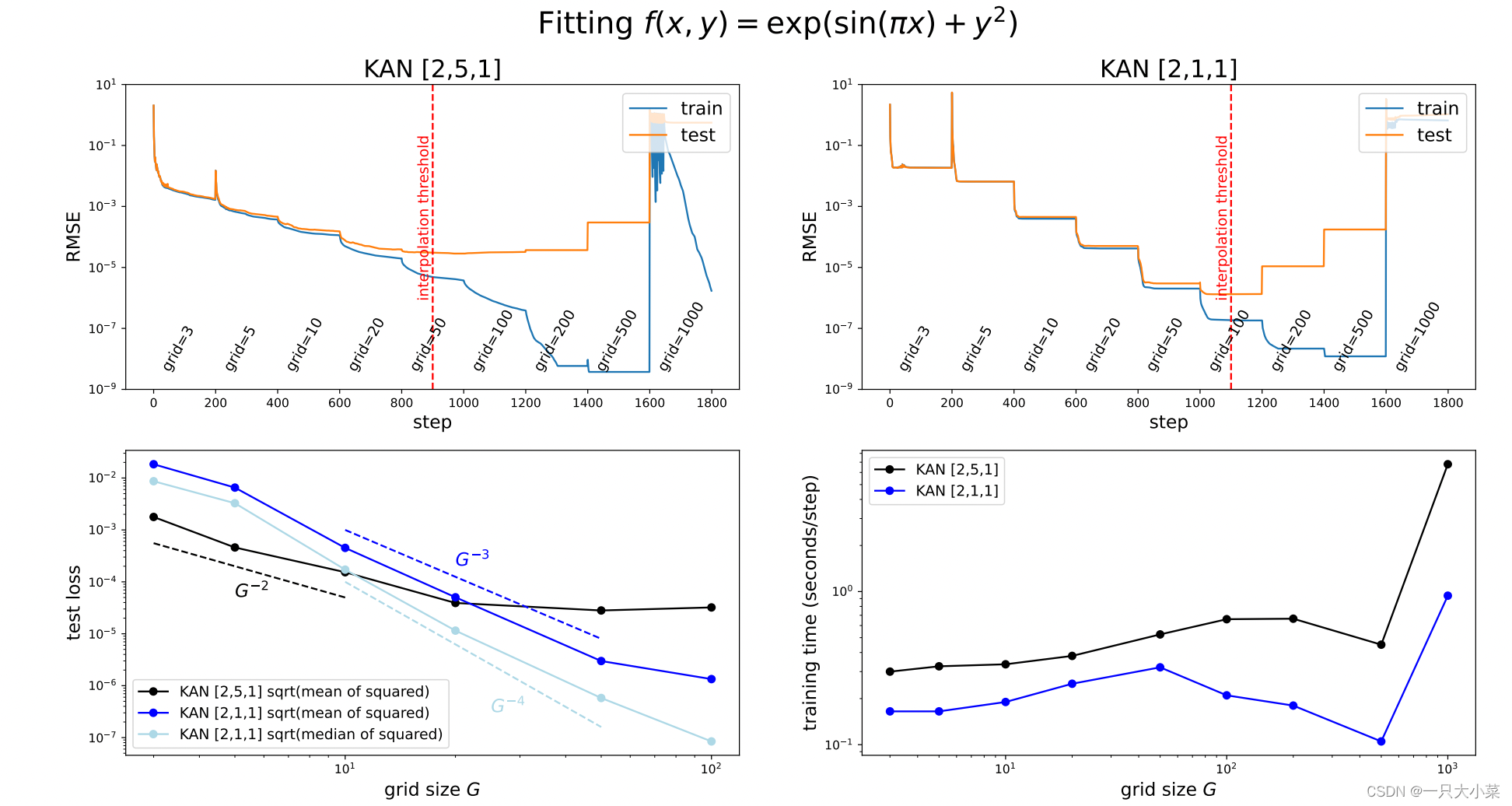
请添加图片描述

如何扩展，待更新

为了可解释性：简化 KAN 并使其具有交互性

稀疏化（Sparsification）：
对于KAN中的激活函数进行稀疏化处理，通常通过L1正则化来实现。由于KAN中没有传统的线性权重，而是使用一维函数，因此需要对这些函数的稀疏性进行特别定义和优化。
可视化（Visualization）：
通过将激活函数的重要性（例如，它们的输出影响程度）可视化，可以帮助研究者和开发者更好地理解模型的工作原理。这种可视化通常包括调整激活函数图像的透明度来反映其相对重要性。
剪枝（Pruning）：
在训练过程中或训练后对模型进行剪枝，移除不重要的节点或激活函数，从而减少模型的复杂性。剪枝后的模型通常更加高效，且更易于分析和部署。
符号化（Symbolification）：
将一些激活函数设置为特定的数学函数（如正弦、指数等），而不是完全依赖数据驱动的方式。这种方法有助于提升模型的数学解释性，使其输出更加可预测。