⚠申明: 未经许可,禁止以任何形式转载,若要引用,请标注链接地址。 全文共计7267字,阅读大概需要3分钟
🌈更多学习内容, 欢迎👏关注👀【文末】我的个人微信公众号:不懂开发的程序猿
个人网站:https://jerry-jy.co/❗❗❗知识付费,🈲止白嫖,有需要请后台私信或【文末】个人微信公众号联系我
语音识别--光谱门控降噪
- 光谱门控降噪
- 一、任务需求
- 二、任务目标
- 1、在噪声音频剪辑上计算 FFT
- 2、通过噪声的 FFT 计算频率数据
- 3、根据噪声的统计数据(以及算法的所需灵敏度)计算阈值
- 4、对信号计算 FFT
- 5、通过将信号 FFT 与阈值进行比较来确定掩膜
- 6、使用滤波器在频率和时间上平滑掩膜
- 7、掩码应用于信号的 FFT,并反转
- 三、任务环境
- 1、jupyter开发环境
- 2、python3.6
- 3、tensorflow2.4
- 四、任务实施过程
- 加载工具
- 1、加载数据
- 2、添加噪音
- 3、去噪
- 五、任务小结
- 说明
光谱门控降噪
一、任务需求
本降噪方法使用了audacity的降噪方法
该降噪方法使用 Python 实现,可以降低语音、生物声学和生理信号等时域信号中的噪声。它依赖于一种称为“频谱门控”的方法,这是一种噪声门控方法。它的工作原理是计算信号(以及可选的噪声信号)的频谱图并估计该信号/噪声的每个频带的噪声阈值(或门)。该阈值用于计算掩码,该掩码将噪声选入频率变化阈值以下。
本方法要求两个输入:
原型噪声音频
要去除的信号
要求:使用audacity的降噪方法对音频进行降噪
二、任务目标
1、在噪声音频剪辑上计算 FFT
2、通过噪声的 FFT 计算频率数据
3、根据噪声的统计数据(以及算法的所需灵敏度)计算阈值
4、对信号计算 FFT
5、通过将信号 FFT 与阈值进行比较来确定掩膜
6、使用滤波器在频率和时间上平滑掩膜
7、掩码应用于信号的 FFT,并反转
三、任务环境
1、jupyter开发环境
2、python3.6
3、tensorflow2.4
四、任务实施过程
实验步骤
- 在噪声音频剪辑上计算 FFT
- 通过噪声的 FFT 计算频率数据
- 根据噪声的统计数据(以及算法的所需灵敏度)计算阈值
- 对信号计算 FFT
- 通过将信号 FFT 与阈值进行比较来确定掩码
- 使用过滤器在频率和时间上平滑蒙版
- 掩码应用于信号的 FFT,并反转
加载工具
import IPython
from scipy.io import wavfile
import scipy.signal
import numpy as np
import matplotlib.pyplot as plt
import librosa
%matplotlib inline
1、加载数据
原始语音内容如下:
"I know the human being and fish can coexist peacefully."
– Saginaw, Michigan, September 29, 2000
wav_loc = "/home/jovyan/datas/fish.wav"
rate, data = wavfile.read(wav_loc)
data = data / 32768
IPython.display.Audio(data=data, rate=rate)
fig, ax = plt.subplots(figsize=(20,4))
ax.plot(data)
[<matplotlib.lines.Line2D at 0x7f564b8feb00>]
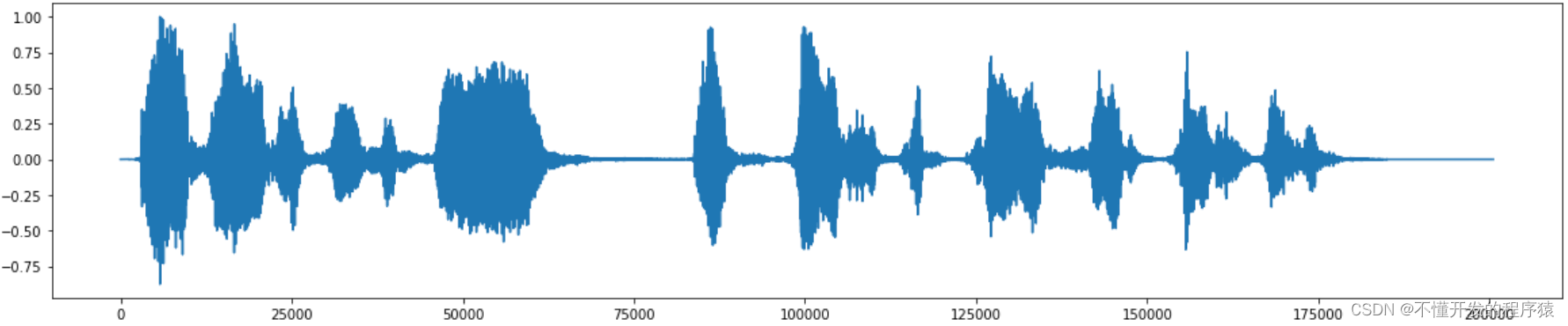
上图显示的是该语音对应的波形,横坐标是采样点
2、添加噪音
定义噪声生成器
- 使用快速傅里叶变换生成噪声
- 生成带限噪声
def fftnoise(f):
f = np.array(f, dtype="complex")
Np = (len(f) - 1) // 2
phases = np.random.rand(Np) * 2 * np.pi
phases = np.cos(phases) + 1j * np.sin(phases)
f[1 : Np + 1] *= phases
f[-1 : -1 - Np : -1] = np.conj(f[1 : Np + 1])
return np.fft.ifft(f).real
def band_limited_noise(min_freq, max_freq, samples=1024, samplerate=1):
freqs = np.abs(np.fft.fftfreq(samples, 1 / samplerate))
f = np.zeros(samples)
f[np.logical_and(freqs >= min_freq, freqs <= max_freq)] = 1
return fftnoise(f)
生成噪声,并在原始音频上添加噪声
noise_len = 2 # 单位:秒
# 使用自定义函数生成噪声
noise = band_limited_noise(min_freq=4000, max_freq = 12000, samples=len(data), samplerate=rate)*30
# 将噪声裁剪成和原始音频同样长
noise_clip = noise[:rate*noise_len]
# 将噪声与原始音频叠加
audio_clip_band_limited = data+noise
演示添加噪声后的音频数据
fig, ax = plt.subplots(figsize=(20,4))
ax.plot(audio_clip_band_limited)
IPython.display.Audio(data=audio_clip_band_limited, rate=rate)
可以看到,添加噪声以后,声音的波形明显受到干扰,听起来也不够清楚。
3、去噪
自定义相关函数,用于降噪及演示降噪的过程
import time
from datetime import timedelta as td
# 短时傅立叶变换
def _stft(y, n_fft, hop_length, win_length):
return librosa.stft(y=y, n_fft=n_fft, hop_length=hop_length, win_length=win_length)
# 逆短时傅立叶变换
def _istft(y, hop_length, win_length):
return librosa.istft(y, hop_length, win_length)
# 将幅度谱图转换为 dB 标度的谱图。
def _amp_to_db(x):
return librosa.core.amplitude_to_db(x, ref=1.0, amin=1e-20, top_db=80.0)
# 将 dB 标度的谱图转换为幅度谱图。
def _db_to_amp(x,):
return librosa.core.db_to_amplitude(x, ref=1.0)
# 绘制频谱图
def plot_spectrogram(signal, title):
fig, ax = plt.subplots(figsize=(20, 4))
cax = ax.matshow(
signal,
origin="lower",
aspect="auto",
cmap=plt.cm.seismic,
vmin=-1 * np.max(np.abs(signal)),
vmax=np.max(np.abs(signal)),
)
fig.colorbar(cax)
ax.set_title(title)
plt.tight_layout()
plt.show()
# 绘制统计量及滤波器
def plot_statistics_and_filter(
mean_freq_noise, std_freq_noise, noise_thresh, smoothing_filter
):
fig, ax = plt.subplots(ncols=2, figsize=(20, 4))
plt_mean, = ax[0].plot(mean_freq_noise, label="Mean power of noise")
plt_std, = ax[0].plot(std_freq_noise, label="Std. power of noise")
plt_std, = ax[0].plot(noise_thresh, label="Noise threshold (by frequency)")
ax[0].set_title("Threshold for mask")
ax[0].legend()
cax = ax[1].matshow(smoothing_filter, origin="lower")
fig.colorbar(cax)
ax[1].set_title("Filter for smoothing Mask")
plt.show()
# 定义降噪函数
def removeNoise(
audio_clip,
noise_clip,
n_grad_freq=2,
n_grad_time=4,
n_fft=2048,
win_length=2048,
hop_length=512,
n_std_thresh=1.5,
prop_decrease=1.0,
verbose=False,
visual=False,
):
"""根据仅包含噪声的剪辑从音频中去除噪声
参数:
audio_clip(数组):第一个参数。
noise_clip(数组):第二个参数。
n_grad_freq (int):使用掩码平滑处理多少个频率通道。
n_grad_time (int):用掩码平滑的时间通道数。
n_fft (int):STFT 列之间的帧数。
win_length (int): 每帧音频都被 window() 窗口化。窗口的长度为“win_length”,然后用零填充以匹配“n_fft”。
hop_length (int):STFT 列之间的帧数。
n_std_thresh (int):比噪声的平均 dB(在每个频率级别)大多少个标准偏差被视为信号
prop_decrease (float): 你应该在多大程度上减少噪音(1 = 全部,0 = 无)
visual (bool): 是否绘制算法的步骤
返回:
数组:减去噪声的恢复信号
"""
if verbose:
start = time.time()
# 对噪声应用短时傅里叶变换
noise_stft = _stft(noise_clip, n_fft, hop_length, win_length)
noise_stft_db = _amp_to_db(np.abs(noise_stft)) # 转换为dB频谱
# 对噪声计算均值、标准差统计量
mean_freq_noise = np.mean(noise_stft_db, axis=1)
std_freq_noise = np.std(noise_stft_db, axis=1)
noise_thresh = mean_freq_noise + std_freq_noise * n_std_thresh
if verbose:
print("STFT on noise:", td(seconds=time.time() - start))
start = time.time()
# 对信号应用短时傅里叶变换
if verbose:
start = time.time()
sig_stft = _stft(audio_clip, n_fft, hop_length, win_length)
sig_stft_db = _amp_to_db(np.abs(sig_stft))
if verbose:
print("STFT on signal:", td(seconds=time.time() - start))
start = time.time()
# 计算dB频谱掩码
mask_gain_dB = np.min(_amp_to_db(np.abs(sig_stft)))
print(noise_thresh, mask_gain_dB)
# 在时间和频率上为掩码创建平滑过滤器
smoothing_filter = np.outer(
np.concatenate(
[
np.linspace(0, 1, n_grad_freq + 1, endpoint=False),
np.linspace(1, 0, n_grad_freq + 2),
]
)[1:-1],
np.concatenate(
[
np.linspace(0, 1, n_grad_time + 1, endpoint=False),
np.linspace(1, 0, n_grad_time + 2),
]
)[1:-1],
)
smoothing_filter = smoothing_filter / np.sum(smoothing_filter)
# 计算每个频率/时间窗的阈值
db_thresh = np.repeat(
np.reshape(noise_thresh, [1, len(mean_freq_noise)]),
np.shape(sig_stft_db)[1],
axis=0,
).T
# 如果信号高于阈值则屏蔽
sig_mask = sig_stft_db < db_thresh
if verbose:
print("Masking:", td(seconds=time.time() - start))
start = time.time()
# 使用平滑滤波器对掩码进行卷积
sig_mask = scipy.signal.fftconvolve(sig_mask, smoothing_filter, mode="same")
sig_mask = sig_mask * prop_decrease
if verbose:
print("Mask convolution:", td(seconds=time.time() - start))
start = time.time()
# 对信号应用掩码
sig_stft_db_masked = (
sig_stft_db * (1 - sig_mask)
+ np.ones(np.shape(mask_gain_dB)) * mask_gain_dB * sig_mask
) # 对真实值进行掩码
sig_imag_masked = np.imag(sig_stft) * (1 - sig_mask)
sig_stft_amp = (_db_to_amp(sig_stft_db_masked) * np.sign(sig_stft)) + (
1j * sig_imag_masked
)
if verbose:
print("Mask application:", td(seconds=time.time() - start))
start = time.time()
# 修复信号
recovered_signal = _istft(sig_stft_amp, hop_length, win_length)
recovered_spec = _amp_to_db(
np.abs(_stft(recovered_signal, n_fft, hop_length, win_length))
)
if verbose:
print("Signal recovery:", td(seconds=time.time() - start))
if visual:
plot_spectrogram(noise_stft_db, title="Noise")
if visual:
plot_statistics_and_filter(
mean_freq_noise, std_freq_noise, noise_thresh, smoothing_filter
)
if visual:
plot_spectrogram(sig_stft_db, title="Signal")
if visual:
plot_spectrogram(sig_mask, title="Mask applied")
if visual:
plot_spectrogram(sig_stft_db_masked, title="Masked signal")
if visual:
plot_spectrogram(recovered_spec, title="Recovered spectrogram")
return recovered_signal
output = removeNoise(audio_clip=audio_clip_band_limited, noise_clip=noise_clip,verbose=True,visual=True)
上图依次为我们演示了:
- 噪声的频谱图
- 计算的掩膜的阈值
- 用于平滑掩膜的滤波器
- 原始信号对应的频谱图
- 计算得到的掩膜频谱图
- 经过掩膜处理的信号频谱图
- 经过恢复后的声音信号频谱图
最后我们观察一下降噪以后得到的声音结果
fig, ax = plt.subplots(nrows=1,ncols=1, figsize=(20,4))
plt.plot(output, color='black')
ax.set_xlim((0, len(output)))
plt.show()
# 播放声音样本
IPython.display.Audio(data=output, rate=44100)
五、任务小结
本实验完成光谱门控降噪方法对声音进行降噪处理。通过本实验我们学习到了光谱门控降噪的相关知识,需要掌握以下知识点:
- 通过噪声的傅里叶变换计算得到噪声相关特征
- 通过对信号计算傅里叶变换,确定阈值,从而确定掩膜/掩码
- 对声音掩膜应用滤波器,实现降噪
–end–
说明
本实验(项目)/论文若有需要,请后台私信或【文末】个人微信公众号联系我