亏了亏了！双向孟德尔随机化阴性结果居然发了SCI二区（IF=6.7）

news2024/10/5 18:31:50

‍

今天为诸位介绍的这篇文章是一项双向孟德尔随机化研究（MR），惊讶的是，双向因果均为阴性结果发了SCI二区！我们一起来看看！

2024年4月17日，广东医科大学附属医院的学者做了一项双向两样本孟德尔随机化研究，在期刊Thrombosis And Haemostasis（医学二区，IF=6.7）发表了题为：“The Association between Obstructive Sleep Apnea and Venous Thromboembolism: A Bidirectional Two-Sample Mendelian Randomization Study”的研究论文，本研究旨在利用大规模全基因组关联研究(GWAS)公开的汇总统计数据进行双向两样本孟德尔随机化分析，从遗传学角度评估阻塞性睡眠呼吸暂停(OSA)与静脉血栓栓塞(VTE)(包括深静脉血栓形成(DVT)和肺栓塞(PE))之间的确切关联。

本公众号回复“ 原文”即可获得文献PDF等资料

尽管之前的观察性研究已经调查了OSA和静脉血栓栓塞之间的潜在关联，但由于潜在混杂因素和反向因果偏倚的局限性，从这些研究中阐明这种关联的各个方面具有挑战性。

主要研究结果

1.研究设计

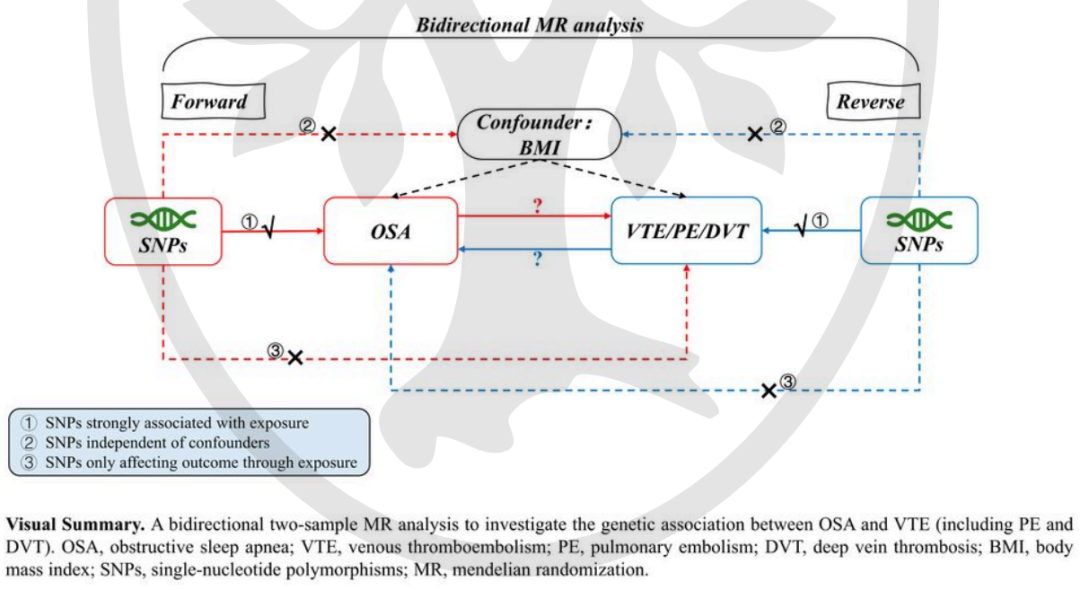
MR利用遗传变异，主要是SNPs作为工具变量(IVs)来研究暴露与结果之间的遗传关联。MR基于三个基本假设:

(1)遗传变异与暴露高度相关;

(2)遗传变异不受潜在混杂因素的影响;

(3)基因变异仅通过暴露影响结果。

只有当这些假设满足时，IVs才被认为是有效的。本研究采用双向两样本MR分析来评估OSA和VTE之间的遗传关联。

首先，与OSA相关的SNP被用来检查它们对VTE的影响。
随后，为了研究反向关联的可能性，采用符合条件的IVs来量化VTE对OSA的影响。

阻塞性睡眠呼吸暂停(OSA)的定义基于主观症状、临床检查和睡眠登记，应用呼吸暂停低通气指数≥5/小时或呼吸事件指数≥5/小时。

静脉血栓栓塞(VTE)被定义为一种包括PE(肺动脉或其分支被栓塞)和DVT(深静脉血栓形成)的疾病。

2.IVs的选择标准

VTE(包括PE和DVT)的全基因组显著SNP阈值设置为P<5.0×10-8，而OSA的阈值调整为P<1×10-5（因为无法使用P<5.0×10-8的显著性水平检测OSA相关SNP）。
排除具有连锁不平衡效应的SNP(在10,000kb窗口内r2<0.001)，以确保所选IVs的独立性。
使用F-statistic [F-statistic=(beta/se)2]来测量IVs与暴露之间的关联强度。保留f统计量>10的SNP，以避免弱工具偏倚的影响。
在协调过程中，去除与结果不匹配的SNP以及等位基因频率不明确的回文SNP(0.42-0.58)。
既往研究表明，肥胖是OSA和静脉血栓栓塞的危险因素。通过Phenoscanner (http://www.phenoscanner.medschl.cam.ac.uk/)查询并排除与体重指数(BMI)相关的SNP。

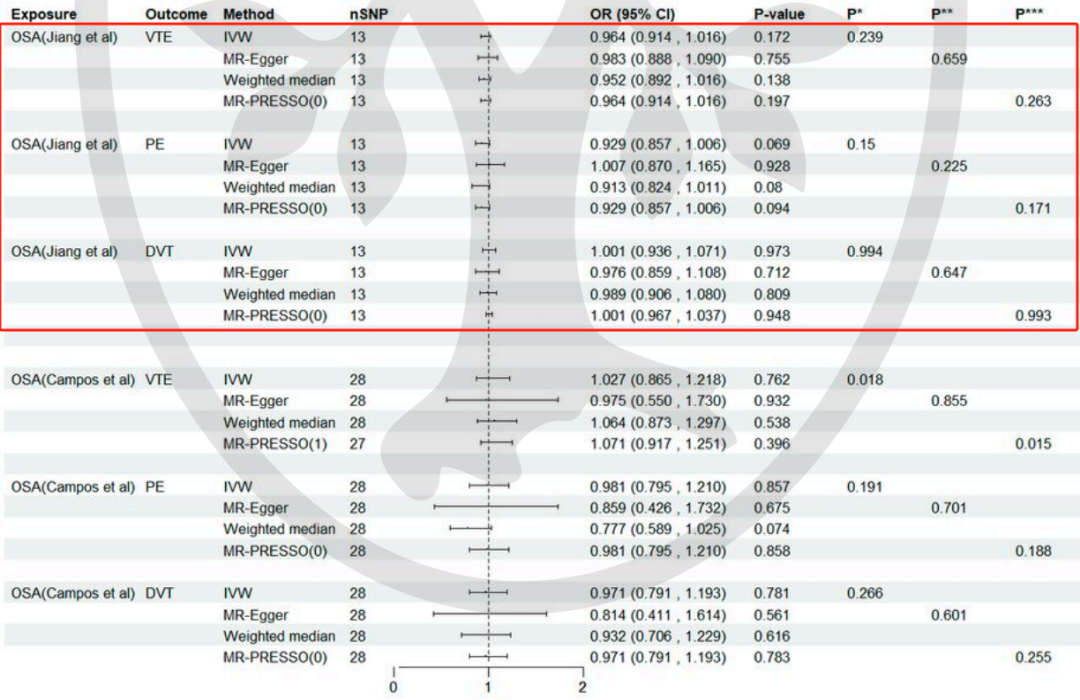
3.OSA与VTE、PE和DVT风险之间无显著关联

在初始MR分析中：

随机效应IVW方法显示OSA与VTE、PE和DVT风险之间无显著关联。
Cochran Q检验未发现异质性，MR-Egger截距检验和MR-PRESSO全局检验均未发现任何多效性的证据。

使用OSA遗传变异的验证分析(Campos等)也得到了类似的结果。三种互补的MR方法均不支持OSA和VTE之间的遗传关联。

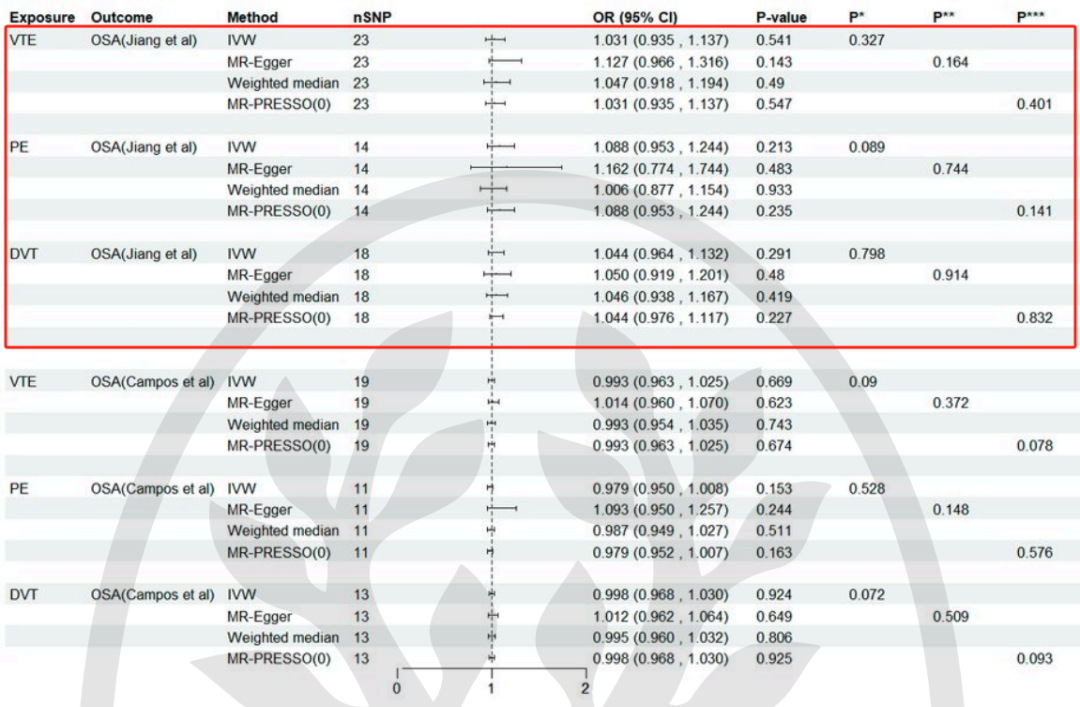
4.VTE对OSA的影响

为了进一步评估VTE(包括PE和DVT)对OSA的影响，我们进行了反向MR分析。两种MR分析都得出了一致的结果，表明VTE、PE和DVT对OSA没有显著影响。

Cochran Q检验未发现异质性， MR-Egger截距检验和MR-PRESSO全局检验均未发现多效性。

总之，一系列敏感性证实了MR结果的可靠性。

统计学方法

本文统计方法简单，就是双向孟德尔随机化：

采用乘法随机效应逆方差加权(IVW)方法作为MR分析的主要方法，以评估OSA与VTE之间的遗传关联。
为了确保结果的有效性和稳健性，使用另外三种MR方法进行敏感性分析，即MR- egger、加权中位数和MR多效性残差和异常值(MR- presso)。

IVW方法荟萃分析了每个SNP对结果的Wald比值估计值，当所有选择的SNP都是有效的IVs时，提供了对因果效应的精确估计。然而，IVW方法对因果效应的估计可能因多效IVs的影响而有偏差。
不同的是，即使在所有IVs无效的情况下，MR-Egger方法也能够产生可靠的因果估计。此外，MR-Egger提供了截距检验来检测水平多效性，显著性阈值P < 0.05表明存在水平多效性。
与IVW和MR-Egger方法相比，加权中位数方法显示出更强的稳健性，并提供了一致的因果效应估计，即使高达50%的IVs是无效工具。
MR-PRESSO方法识别具有潜在水平多效性的异常值，并在去除异常值后提供估计，其中整体检验的P < 0.05表明存在具有水平多效性的异常值。
采用Cochran Q检验检验异质性，P < 0.05为显著性阈值，异质性显著。