目录
- 一、说明
- 二、处理有限的、大尺度的母体抽样
- 三、非参数的估计
- 四、连续母体抽样技巧--分箱
一、说明
对于抽样问题,前几期文章都是理论探讨。本篇给出若干示例,展现具体的情况下,面对数据,如何给出处理策略。
二、处理有限的、大尺度的母体抽样
【问题1】一所大学有3000名男生,身高服从均值为68.8英寸,标准差为3.0英寸的正态分布。设计抽样为80组样本,每组25名学生。
问题:1)有放回抽样。2)无放回抽样。问抽样均值抽样的均值和标准差是多少?
分析:抽样分布的空间:
在有放回抽样中,样本分布的抽样组数量是
300
0
2
5
3000^25
300025,显然数量庞大。
在不放回抽样中,样本分布的抽样组数量是
C
3000
25
C_{3000}^{25}
C300025,显然数量庞大。
因此,大数定律成立。
无论是有放回抽样中,还是不放回抽样中,抽样分布的样本数量远远高于80,因此,真实的的抽样分布无法获得,只能获得经验的抽样分布。
1)对于有限母体,无放回抽样,以下公式成立
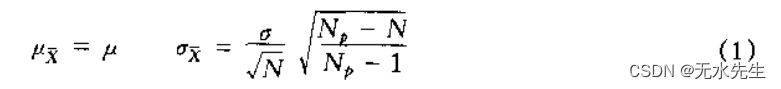
μ
x
ˉ
=
μ
=
68.0
\mu_{\bar{x}}=\mu=68.0
μxˉ=μ=68.0
σ
x
ˉ
=
σ
N
=
σ
N
N
p
−
N
N
p
−
1
=
3
25
3000
−
25
3000
−
1
=
0.6
\sigma_{\bar{x}}=\frac{\sigma}{\sqrt{N}}=\frac{\sigma}{\sqrt{N}}\sqrt{\frac{N_p-N}{N_p-1}}=\frac{3}{\sqrt{25}}\sqrt{\frac{3000-25}{3000-1}}=0.6
σxˉ=Nσ=NσNp−1Np−N=2533000−13000−25=0.6
2)对于有限母体,有放回抽样,以下公式成立
μ
x
ˉ
=
μ
\mu_{\bar{x}}=\mu
μxˉ=μ
σ
x
ˉ
=
σ
N
\sigma_{\bar{x}}=\frac{\sigma}{\sqrt{N}}
σxˉ=Nσ
μ
x
ˉ
=
μ
=
68.0
\mu_{\bar{x}}=\mu=68.0
μxˉ=μ=68.0;
σ
x
ˉ
=
4
25
=
0.6
\sigma_{\bar{x}}=\frac{4}{\sqrt{25}}=0.6
σxˉ=254=0.6
结论:
1)对于大容量的有限母体,因为抽样分布过于庞大,可以按无限母体处理。
2)对于大容量的抽样分布,有放回和无放回抽样区别不大。
3)上述样本均值的经验分布,可近似看成均值为68.8英寸,标准差为0,6的正态分布。
三、非参数的估计
注意,抽样的参数估计并不是我们最后的目的,最后的目的是在样本参数估计的基础上,发掘出更多的特点。
【问题2】在问题1中,在80个样本中,能够找到几个样本抽样,它们的特征是1)均值在66.8英寸和68.3英寸之间 2)均值小于66.4英寸。
【分析】
抽样分布的整体很大,因此无法穷举,因此,抽样分布也是一个估计而已。
通过上述计算,均值抽样满足
N
(
68
,
0.
6
2
)
N(68,0.6^2)
N(68,0.62)的正态分布。
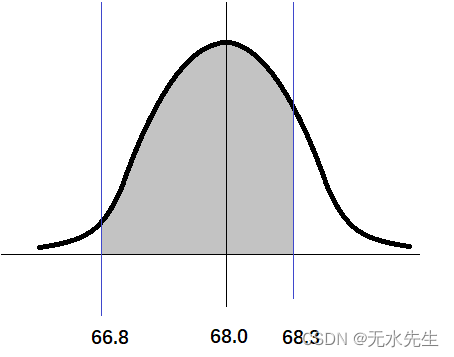
因此,按照抽样分布中,均值抽样的样本落在【66.8,68.3】的概率是:
P
(
66.8
⩽
x
⩽
68.3
)
P(66.8\leqslant x \leqslant 68.3)
P(66.8⩽x⩽68.3)。
以上是个非标准的,转化成标准正态分布后,可以查表得到P;通过s=P*80可以得到满足以上所条件的抽样数s。
【解决】样本标准化,一般指向以下步骤:
z
=
X
ˉ
−
μ
X
ˉ
σ
X
ˉ
=
X
ˉ
−
68.0
0.6
z=\frac{\bar{X}-\mu_{\bar{X}}}{\sigma_{\bar{X}}}=\frac{\bar{X}-68.0}{0.6}
z=σXˉXˉ−μXˉ=0.6Xˉ−68.0
66.8
的标准值
=
66.8
−
68.0
0.6
=
−
2
66.8的标准值=\frac{66.8-68.0}{0.6}=-2
66.8的标准值=0.666.8−68.0=−2
68.3
的标准值
=
68.4
−
68.0
0.6
=
0.5
68.3的标准值=\frac{68.4-68.0}{0.6}=0.5
68.3的标准值=0.668.4−68.0=0.5
从网上随便查找一个标准正态表:
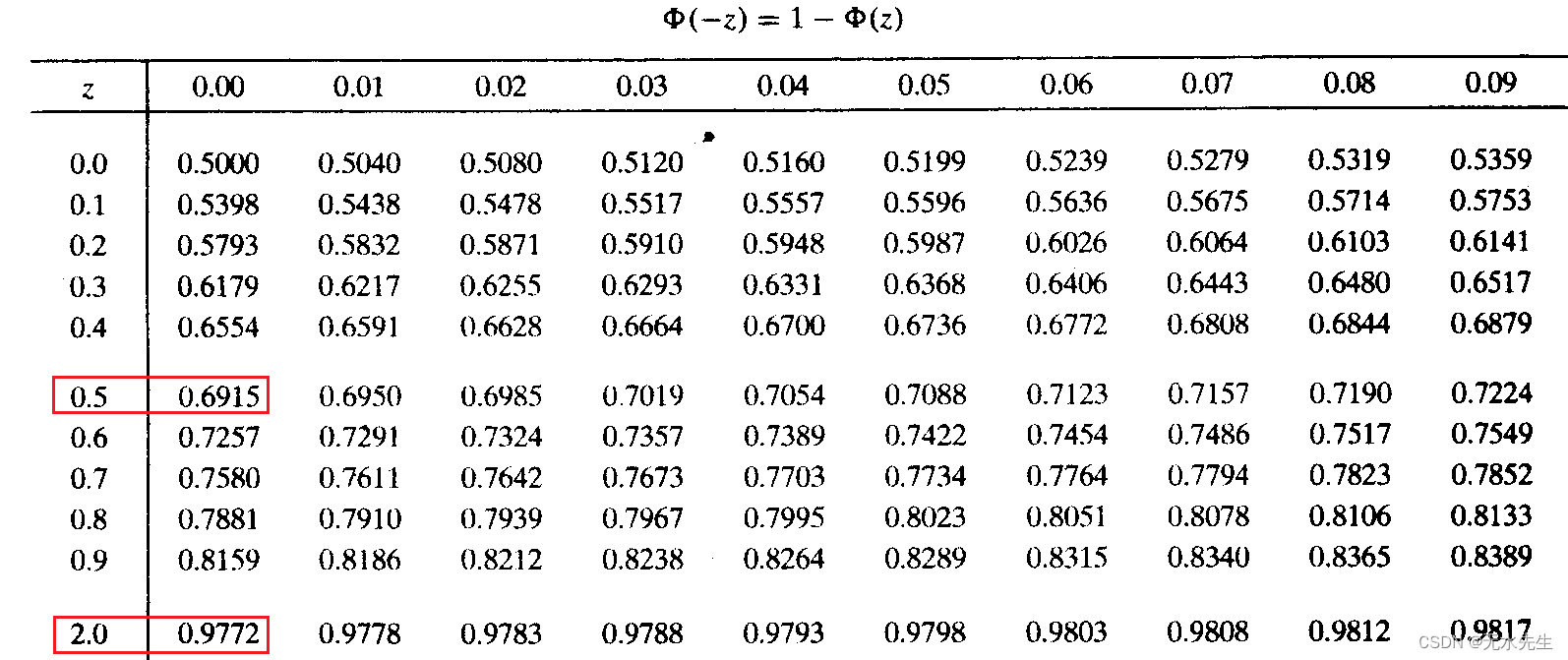
P(-2, 0.5) = 0.6915 - (1-0.9772) = 0.6687
s = 80*0.6687 = 53.49
即在80组抽样中,估计有53个均值在66.8-68.3之间。
四、连续母体抽样技巧–分箱
在数据分析过程中,常常遇到母体是连续分布的情况;按照理论上说,抽样数据在任意区间都应该是无限的,那么如何抽样?答案是用分箱技术,所谓分箱技术,就是将连续无限集合划分成有限集合的过程。这个过程当然是近似的。
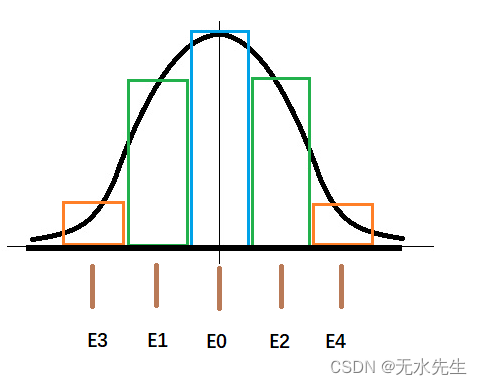
下面举出一个具体示例。
对XYZ大学的100个男生进行抽样。这里母体就是有限100;对母体进行分箱后数据如下:

- 以下是对分箱后的均值计算方法
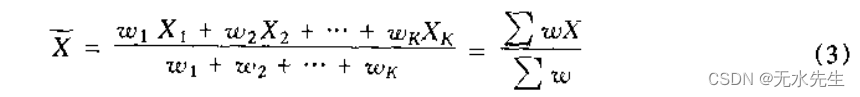
在没有任何信息的情况,均值计算如下:
X ˉ = 0.05 × 61 + 0.18 × 64 + 0.42 × 67 + 0.27 × 70 + 0.08 × 73 0.05 + 0.18 + 0.42 + 0.27 + 0.08 = 67.45 \bar{X}=\frac{0.05\times 61+ 0.18\times64+ 0.42\times67+0.27\times70+0.08\times73}{0.05+0.18+0.42+0.27+0.08}=67.45 Xˉ=0.05+0.18+0.42+0.27+0.080.05×61+0.18×64+0.42×67+0.27×70+0.08×73=67.45
2)在有如下抽样后,如何处理?
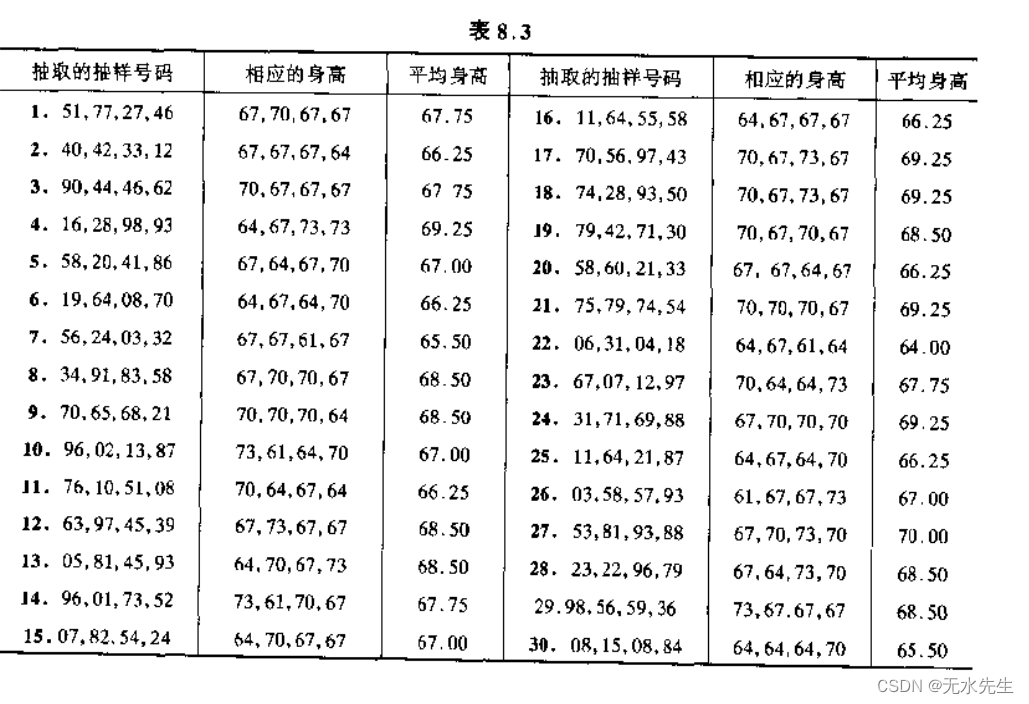
1)均值:通过【 67.75,66.25,67.75,69.25,67.0,66.25,65.5,68.5,68.5,67.0,66.25,68.5,68.5,67.75,67.0,66.25,69.25,69.25,68.5,66.25,69.25,64,67.75,69.25,66.25,67.0,70.0,68.5,68.5,65.5】输入python代码。很容易得到。
import statistics
data = [67.75,66.25,67.75,69.25,67.0,66.25,65.5,68.5,68.5,67.0,66.25,68.5,68.5,67.75,67.0,66.25,69.25,69.25,68.5,66.25,69.25,64,67.75,69.25,66.25,67.0,70.0,68.5,68.5,65.5]
mean = statistics.mean(data)
dev = statistics.pstdev(data)
mean = 67.57
2)标准差
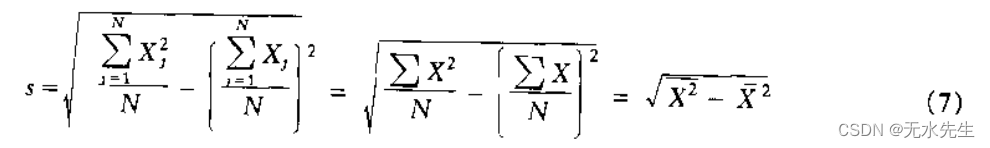
可以得到:
dev=1.40