最近复习了一下十种基本的排序算法，但是发现有很多的细节理解不到位，不是忘了而是根本没理解。就比如为啥有的排序是不稳定排序，而有的排序的时间复杂度高等等问题。

---

---

一、不稳定排序的稳定性分析和复杂度

常见排序算法中有4种排序是不稳定的。快速排序，希尔排序，堆排序， 选择排序。

1. • 快速排序

快速排序是一种不稳定的排序。

1.1什么是快速排序

在一个无序数组里，我们先选择一个基准值(一般选择头一个数作为基准值)，然后创建两指针，以这个基准值为标准，左指针找小于等于基准值的数，右指针找大于基准值的数，找到后，交换两个指针指向的数据，继续往后找，直到两个指针相遇为止，最后交换基准值和两指针共同指向的那个值。

1.2快速排序不稳定的原因

为啥说他不稳定呢，如果说出现两个一样的数，但是后面的数可能排到前面去，所以说他不稳定。

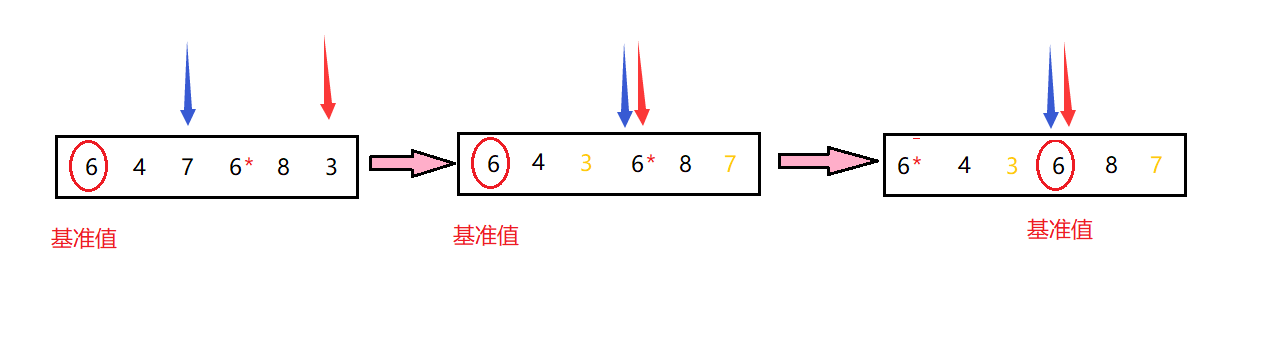
这里我们让小于等于基准值的数都排到基准值的前面了，所以最后6*会在基准值的前面，这样是不是就错了。如果我们把大于等于基准值的数排到基准值的后面就不会出现这样的错误。但是这个错误很可能出现，所以我们说快速排序是不稳定排序。

1.3时间复杂度分析：

最差情况：对于快速排序来说它的最差情况就是每次选择的基准值是数组中的最大值或者是最小值。假设每一次选择的都是最小值，那其他数的位置不变，然后序列的首位置就被固定。继续让剩下的n-1个元素占据2~n的位置，但是每次选择的还是最小值，以此类推。

对于n个数来说，需要操作n层，并且每一层要比较剩下的元素。所以时间复杂度时O(N^2) 。

最好情况：最好的情况就是，基准值正好能把整个无序数列平分成两截。

T(n)=2*T(n/2)+f(n);     T(n/2)是每一个子区间的时间，f(n)是分裂一个区间用的时间。

接下来的操作就和归并排序的一毛一样了。这里我就不再絮了，各位大佬就看最后面的归并排序吧。

时间复杂度是O(nlogn)

---

2.希尔排序

2.1什么是希尔排序

希尔排序是将待排序的数组元素 按下标的一定增量分组（gap） ,分成多个子序列,
然后对各个子序列进行直接插入排序算法排序;
然后依次缩减增量再进行排序,直到增量为1时,进行最后一次直接插入排序,排序结束。

2.2希尔排序不稳定的原因：

这个不稳定的原因还是相同的数据，但是这两个数据的前后顺序改变了。

我用*代表的是相同的两个数，出现的更靠后那个。

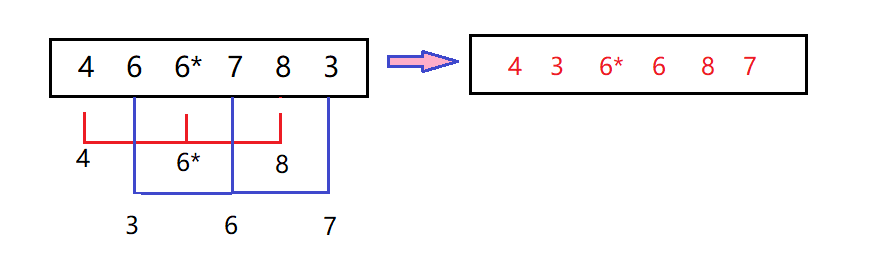
然后gap的距离不断减小，一直到升序排序后，6*一直就会再6的前面了，所以希尔排序也是不稳定的。

2.3希尔排序时间复杂度

增量序列的选择会极大地影响希尔排序的效率。 希尔排序时间复杂度非常难以分析，

它的平均复杂度界于 O(n) 到 O(n^2) 之间，普遍认为它最好的时间复杂度为 O(n^1.3)

希尔排序其实是插入排序的一个优化，而插入排序的时间复杂度是O(n^2)，希尔排序的时间要小于插入排序，也可以这样理解。

---

3.堆排序

3.1啥是堆排序

堆排序有大堆排序和小堆排序两种堆排序方式，小堆排序就是让根节点是最小的，根节点必须小于左右子节点，但是不需要比较左右子节点的大小。只需要保证根节点小于子节点即可。大堆就是让根节点大于左右子节点即可。堆排序的底层是数组来实现的。

3.2堆排序不稳定的原因：

堆排序的根本是不是沿着根节点找叶子节点，并比较两者的值进行相关的交换。但是如果说用相同的两个值出现在一个堆中，就可能造成不稳定性。

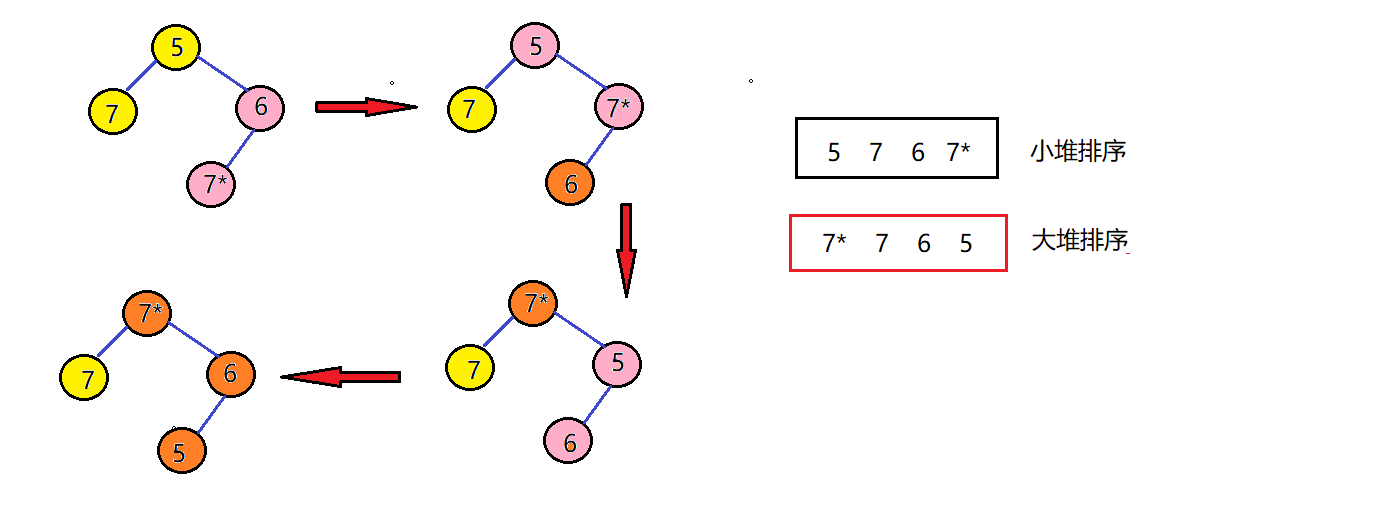
3.3堆排序时间复杂度

这个我就不推导了，各位就记住他是O(nlogn)吧，推导一遍的意义不大，纯属浪费时间。

---

4.选择排序

4.1什么是选择排序

选择排序的工作原理是每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的后面。以此类推，直到全部待排序的数据元素排完。

4.2为啥选择排序不稳定

之所以它不稳定，还是因为重复出现的数据的顺序可能出现改变

有的兄弟可能看不懂是咋比较的，选择排序是选出最小值放在序列最前面，也就是5的位置存放的是最小值。所以挨个比较，然后找到5>1,所以交换5和1--->1 5* 5 7。所以这个排序变得不稳定了。

4.3选择排序的时间复杂度

对于选择排序来说，外层循环决定的是n个位置的归属权，所以要比较n-1次，对于内层循环，最坏的情况是逆序排列，那要比较n-1,n-2...1次，所以他的时间复杂度是O(n^2)

---

5.插入排序的稳定性示范

有的老铁该说，按你说的，那稳定排序也会这样子排列。我们来试一下稳定排序究竟会不会这么排。

我们用插入排序试一下。

5.1什么是插入排序

插入排序就是将无序数组最前面出现的几个数作为一个区间，后面的数如果在区间内，就直接排在区间里，如果大于或者小于这个区间就更新位区间的边界。然后继续插入。

5.2插入排序的稳定

就比如上面的5 7 6 7*，首先把5当作一个区间，然后插入7，5<7,把区间扩展成[5,7],然后插入6，6在区间呢。所以是[5,6,7]，然后插入7*，这个7*和7相等，所以不往区间里面填了，而是把后面的7*作为新的边界处理，所以他是稳定的排序算法。

5.3插入排序的时间复杂度

对于插入排序来说，它的时间复杂度特别好计算，最坏的情况是不是逆序，所以n个数要比较n-1+n-2+n-3+...+2+1=n*(n-1)/2。 同理，它交换的次数也是n*(n-1)/2

所以他的时间复杂度是O(n^2)。

---

6.不稳定性的总结：

综合三种不稳定排序的相关原因来说，都是几个相同的数据进行排序后，后出现的排在了前面，先出现的排在后面。相同的数据的出现次序可能会造成不稳定排序。
切记要注意这是可能会造成，不是一定会造成。

二、稳定排序复杂度分析

1.冒泡排序：

1.1什么是冒泡排序

冒泡排序就是 依次比较相邻两个数字，交换数字，直到最大的数字被排列到序列的最尾部。
它重复地走访过要排序的元素列，依次比较两个相邻的 元素，如果顺序（如从大到小、首字母从Z到A）错误就把他们交换过来。走访元素的工作是重复地进行，直到没有相邻元素需要交换，也就是说该元素列已经排序完成。

1.2冒泡排序和选择排序的区别

在上面我们介绍了一种选择排序，在这我们就不说它俩的相同点了，一说往后就更不好区分了。

区别：(这里我们默认的都是升序排序)

• 选择排序是序列的最前端位置存放的是最小数据，然后让其他数据和这个最小数据比较，如果比最小数据还要小，就跟这个最小数据交换，必须保证序列最前端的是最小元素，找到最小元素后，在找第二小元素。直到完全排序完。

• 冒泡排序是从头开始，相邻的的两个元素依次进行比较大小，较大的元素被交换的右边，然后这个较大的元素再和其右边的元素进行比较，直到最大元素被交换到序列的最右边。这时我们就在比较剩余的n-1个元素就行了。

• 最简单的一句话就是选择排序进行单挑，冒泡排序进行车轮战。

1.3冒泡排序的复杂度

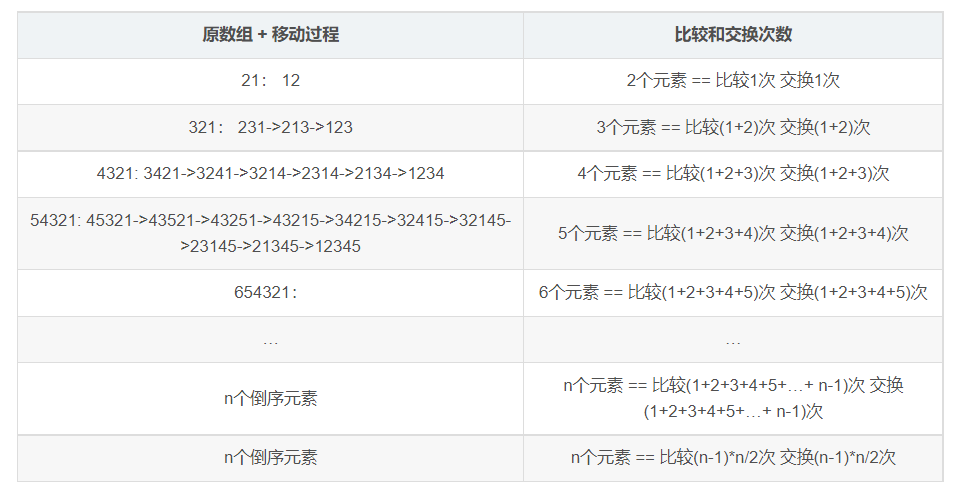
冒泡排序的 最差时间复杂度是：(n-1)*n/2 + (n-1)*n/2 = n^2 -n 忽略低次幂得到 O(n^2)

这是最差的情况，最好的情况是升序排序，只需要进行比较，不需要进行交换。所以是n个元素比较n-1次，时间复杂度是O(n)。这个是flag判断外层循环后，数据有没有发生交换，没交换说明原本数据是升序。

2.归并排序

将已有序的子序列 合并，得到完全有序的 序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为 二路归并。

归并操作，也叫归并算法，指的是将两个顺序序列合并成一个顺序序列的方法。

如　设有数列{6，202，100，301，38，8，1}

初始状态：6,202,100,301,38,8,1

第一次归并后：{6,202},{100,301},{8,38},{1}，比较次数：3；逆序次数：1

第二次归并后：{6,100,202,301}，{1,8,38}，比较次数：4； 逆序次数：1+2=3

第三次归并后：{1,6,8,38,100,202,301},比较次数：4； 逆序次数：4+3+3=10

总的比较次数为：3+4+4=11；

逆序数为：1+3+10=14.。

这里我没把数据以个体为单位而是两个进行比较。

最后一步为啥比较次数是4呢，首先是两个子序列首进行比较，6>1,所以1放进数组中，再拿1后面的数和6比较。6<8,把6放到数组中，比较100和8，再把8放到数组中，比较100和38，把38放到数组中，子序列2已经空了，此时我们可以直接把子序列1中剩余的数据直接放到数组里面就行了。

所以此次就比较了4次：6>1,6<8,100>8,100>38。

2.2归并排序的复杂度

归并排序总时间=分解时间+子序列排好序时间+合并时间

无论每个序列有多少数都是折中分解，所以分解时间是个常数，可以忽略不计。

所以归并排序总时间=子序列排好序时间+合并时间；

• 第一次折中分解时间

假设这n个数排序的时间是T(n)，那第一次折中分解的时间T(n)=2*T(n/2),到最后排序好合并时，只需要一个n个数的循环就可完事，所以时间复杂度是n.

T(n)=2*T(n/2)+n;

• 再进行折中分解，此时有四个子序列了。

一个（n/2）序列排序时间=两个(n/4)的序列排序时间+两个(n/4)的序列的合并为一个（n/2）的序列时间T(n/2)=2*T(n/4)+n/2。

 通过化简T(n)=4*T(n/4)+2n

• 第三次折中分解的时间

T(n/4)=2*T(n/8)+n/4
将T(n/4)带入到黄色公式中，
T(n)=4*(2*T(n/8)+n/4)+2n，简化后：T(n)=8*T(n/8)+3n

到最后分解成一个完全二叉树的形式。通过观察可得，合并时间的那个系数和层数有关，是层数-1.所以我们可以根据节点数n求出层数。n个节点的层数是log2n+1，

所以和并部分的时间是log2n+1-1=log2n.

• 那么我们最后一层是不是可以这样表示

T(n)=n*T(1)+(log2n)*n
T(1)=0，那么T(n)=(log2n)*n

所以归并排序的时间复杂度为O(nlog2n)≈ O(nlogn)
我看了好多网上的资料，有的证明是O(nlog2n),有的是O(nlogn), 这里我们就统一一下用后者吧。

三、归纳总结：