看本博客前建议先看一下ST算法解决BMQ问题详解
一,LCA概念
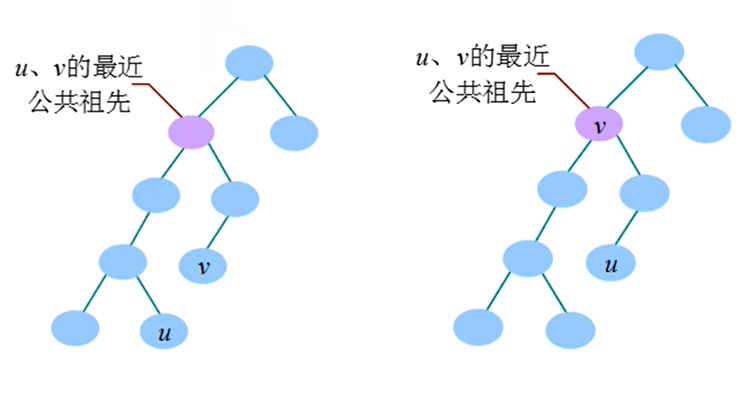
最近公共祖先(Lowest Common Ancestors, LCA)指 有根树中 距离两个
节点最近的 公共祖先。 祖先指 从当前节点到树根路径上的所有节点。
u和v的公共祖先指 一个节点既是 u的祖先,又是 v的祖先。 u和v的最近公共.
祖先指距离 u和v最近的 公共祖先。若v是u的祖先,则u和v的最近公共祖先是v。
比如:
二,解决方法
- 暴力搜索法
暴力搜索法有两种:向上标记法和同步前进法。
1-1向上标记法
从u向上一直到根节点,标记所有经过的节点;若v已被标记,则v节点为
LCA(u, v);否则v也向上走,第1次遇到已标记的节点时,该节点为LCA(u, v)。
1-2同步前进法
将u、v中较深的节点向上走到和深度较浅的节点同一深度,然后两个节点
一起向上走,直到走到同一个节点,该节点就是u、v的最近公共祖先,记作
LCA(u,v)。若较深的节点u到达v的同一深度时,那个节点正好是v,则v节点为
LCA(u,v)。
上述2种方法时间复杂度都为O(n)
在这里给出向上标记法的代码
int LCA(int u,int v)
{
if(u == v) return u;
flag[u] = 1;
while(fa[u] != u)
{//u向上走到根
u = fa[u];
flag[u] = 1;
}
if(flag[v]) return v;
while(fa[v] != v)
{//v向上
v = fa[v];
if(flag[v])
return V;
}
return 0;
}
- 树上倍增法
我们可以设mx[i, j]表示i的2^j辈祖先,即i节点向根节点走2^j步到达的节点。
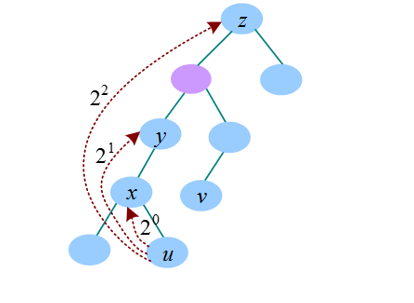
那么状态转移方程就是
mx[i, j]=mx[mx[i, j-1], j-1]
为什么呢?因为i+2^j不就等于(i+2^(j-1))+2^(j-1)吗?
和前面暴力搜索中的同步前进法一样,先让深度大的节点y向上走到与x同一深度,然后x、y一起向上走。和暴力搜索不同的是,向上走是按照倍增思想走的,每次跳都是2的几次方,不是一步一步向上走的,因此速度较快。(证明:任何十进制都可以转化成二进制,也就是一个一个跳n次也可以转化成跳2^a1+2^a2+……+2^ax次方的形式)
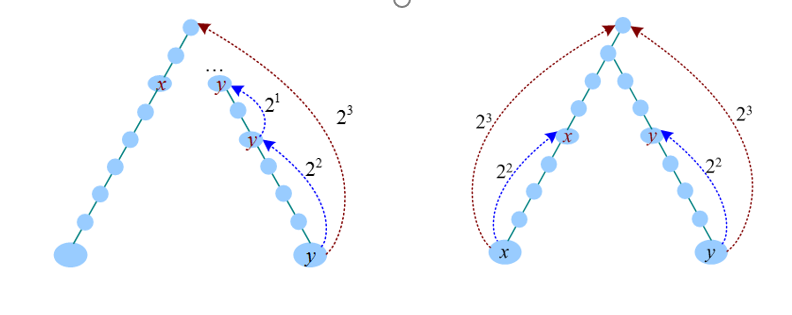
以此题为例:
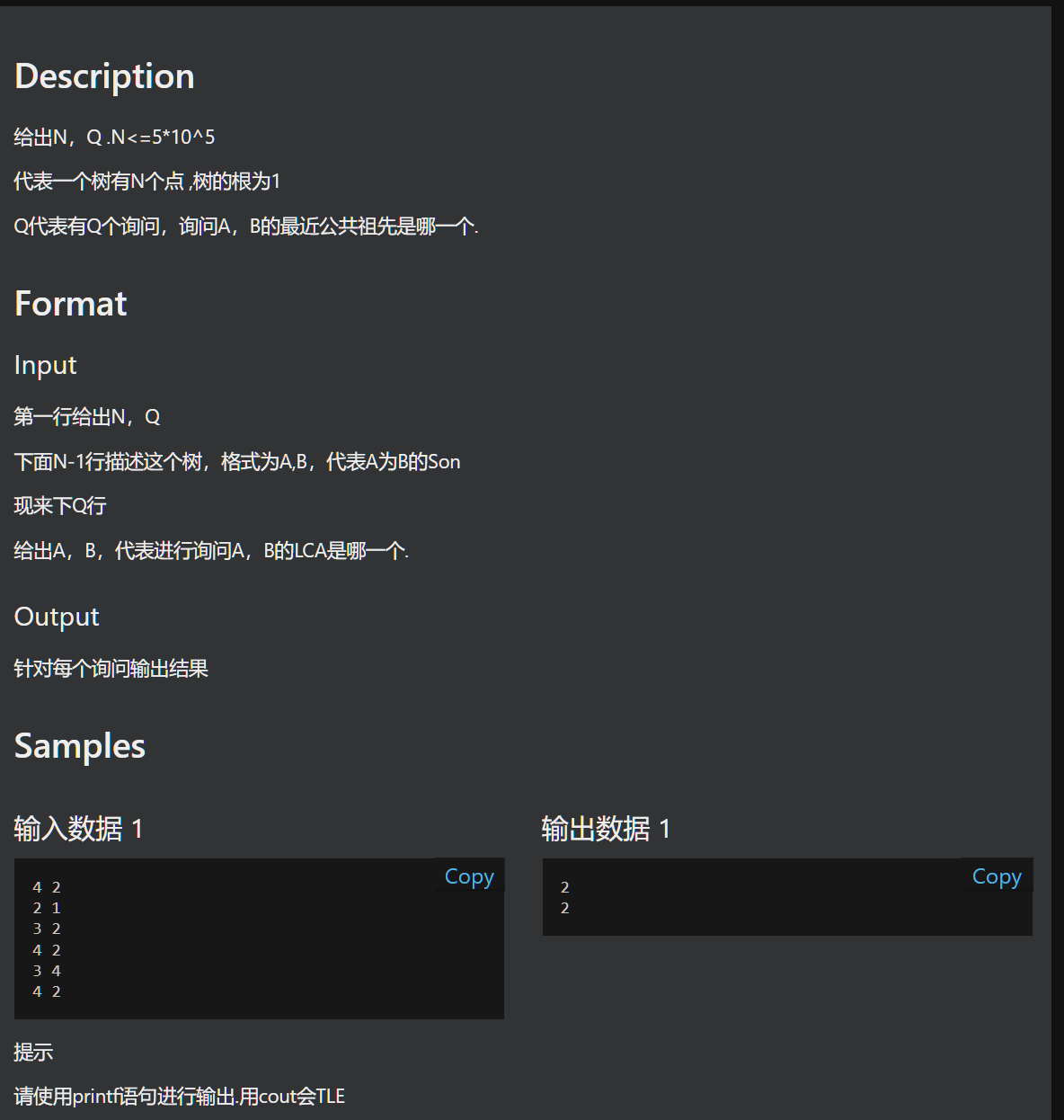
代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,q,u,v;
/*
pre[j]:对于第i条边来说,它的上一条边是哪一条边
now[x]:对于点x来说,最后一条描述它充当父结点的边是哪一条边
son[i]:在第i条边中,充当子结点的点是哪一个
*/
int eg,pre[100001],now[100001],son[100001],deep[100001],mx[1000001][70];
void adeg(int u,int v)
{
pre[++eg] = now[u];
now[u] = eg;
son[eg] = v;
}
void dfs(int u,int fa,int dep)//计算每个点的深度
{
deep[u] = dep;//节点u的深度为dep
for(int i = now[u]; i; i = pre[i])
{
int v = son[i];
if(v == fa) continue;
mx[v][0] = u;//节点v向上跳2^0个位置后节点为u(因为v的父节点就是u)
dfs(v,u,dep + 1);
}
}
int lca(int u,int v)
{
if(deep[u] < deep[v]) swap(u,v);//保证u为u,v中较深的节点
for(int i = 60; i >= 0; i--)
if(deep[mx[u][i]] >= deep[v])
u = mx[u][i];//将u跳到和v同一层
if(u == v) return u;
for(int i = 60; i >= 0; i--)//每次u,v同跳2^i
if(mx[u][i] != mx[v][i])//跳后不能相等,相等的化是公共祖先,但不一定最近
{
u = mx[u][i];
v = mx[v][i];
}
return mx[u][0];//u,v都跳到最近公共祖先的下一层,这样再跳一步就是最近公共祖先了
}
signed main()
{
scanf("%lld%lld",&n,&q);
for(int i = 1; i < n; i++)
{
cin>>u>>v;
adeg(u,v);
adeg(v,u);
}
dfs(1,0,1);
for(int j = 1; j <= 60; j++)
for(int i = 1; i <= n; i++)
mx[i][j] = mx[mx[i][j - 1]][j - 1];
while(q--)
{
scanf("%lld%lld",&u,&v);
printf("%lld\n",lca(u,v));
}
return 0;
}