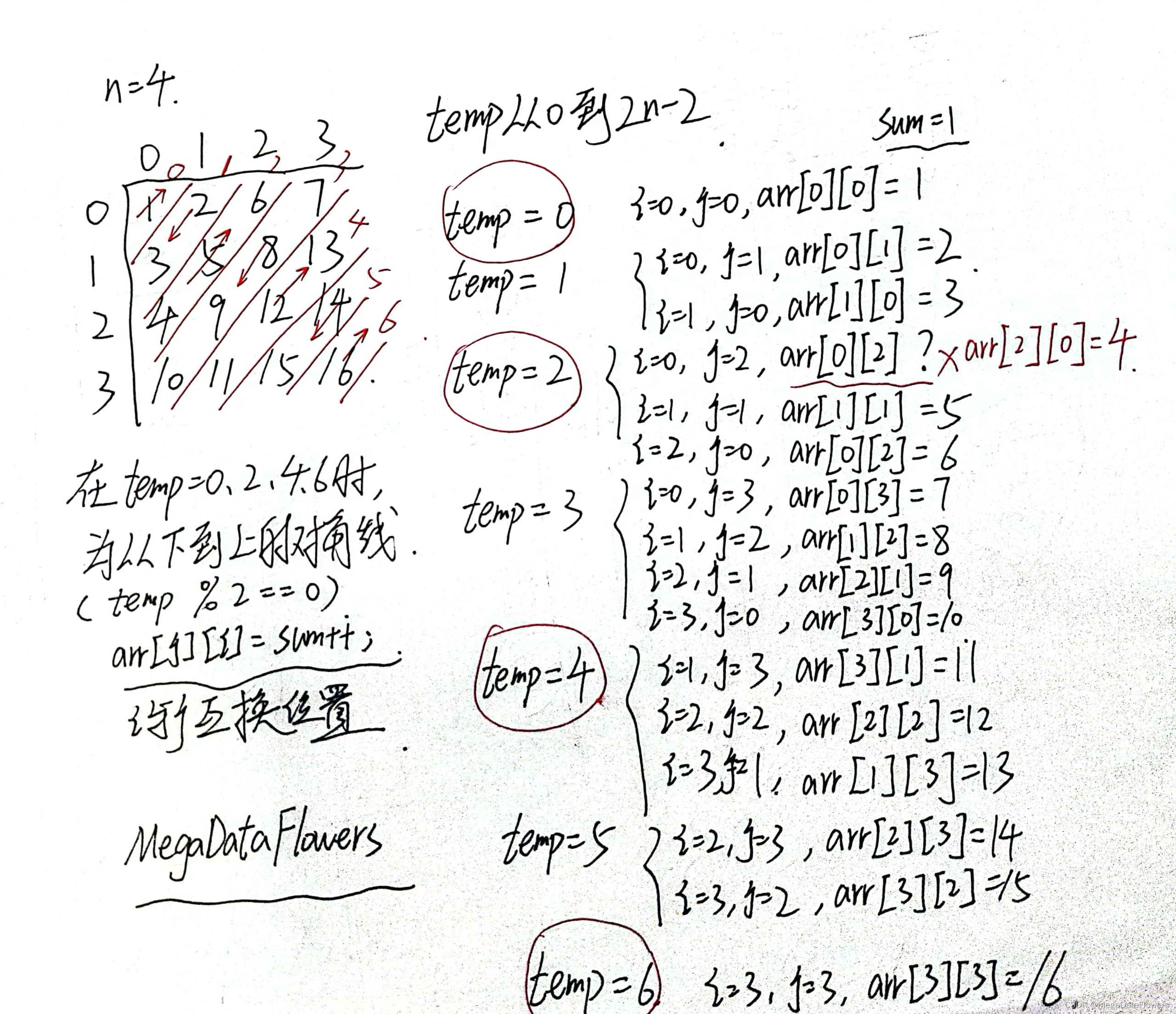题目大意

给定一个区间，构造一个单调不减的序列，使得其前缀异或和与后缀异或和均单调递减，判断这种序列是否存在并输出任意一种解。

思路

暴力 dfs 当然会 TLE,所以我们要仔细分析：

① 在什么情况下异或和能够单调不减？

分析样例，将数字转化成二进制，就是下图：

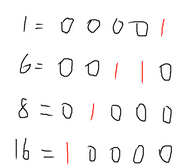
发现没，其实这种序列都有一个特征：每一位二进制位都恰好对应一个数字。这也是这道题的核心。
类似的，我们还可以构造许多这样的序列，比如 3(011),4(100),8(1000),16(10000)。

② 在什么情况下问题有解？

在考虑这个问题之前，首先我们思考：在这样的序列中最后一个元素的最小值是多少？
按照之前的规律，每一位二进制位都恰好对应一个数字，这样我们就可以把第 1 个二进制位给第 1 个数字，第 2 个二进制位给第 2 个数字……直到第 n 个二进制位，给第 n 个数字。发觉没，这些数字不正是 2 的整数幂吗？这个序列 f 的通项公式为：
$f(i)=2^{i-1}(1\le i\le n)$
接下来前面的问题就迎刃而解了，我们只需要判断 ${\log }_{2}m+1$ 是否小于 n，如果小于 n 就无解，否则就将上述序列输出即可。

完整代码

温馨提示：抄袭不是一个好习惯哦~

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n, t, m;
signed main() {
    scanf("%d", &t);
    while(t--) {
    	scanf("%lld%lld", &n, &m);
    	if(log2(m)+1 < n) {puts("No"); continue;}
    	puts("Yes");
    	for(long long i = 1;i < pow(2, n);i *= 2) printf("%lld ", i);
    	puts(""); 
    }
    return 0;
}

summary

这是一道对数学运算的深度理解与灵活运用题