105 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
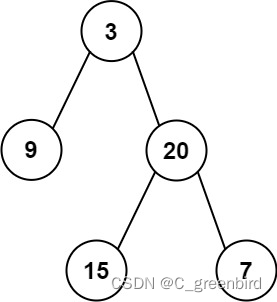
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
提示:
1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证 为二叉树的前序遍历序列
inorder 保证 为二叉树的中序遍历序列
思路
根据先序遍历和中序遍历的特点,我们知道先序遍历的第一个节点就是root,然后在中序遍历中找到root,那么其左边为左子树,右边为右子树。
利用递归实现的过程,假设先序遍历数组preorder的区间为[preL,preR],中序遍历数组inorder的区间为[inL,inR]。那么中间的根节点为preorder[preL],利用k标记找到inorder中的根节点,那么
左子树节点个数为numLeft = k-inL.
左子树的先序遍历区间为[preL+1, preL+numLeft],中序遍历区间为[inL,k-1];
右子树的先序遍历区间为[preL+numLeft+1, preR],中序遍历区间为[k+1,inR].
这样一直递归下去即可。
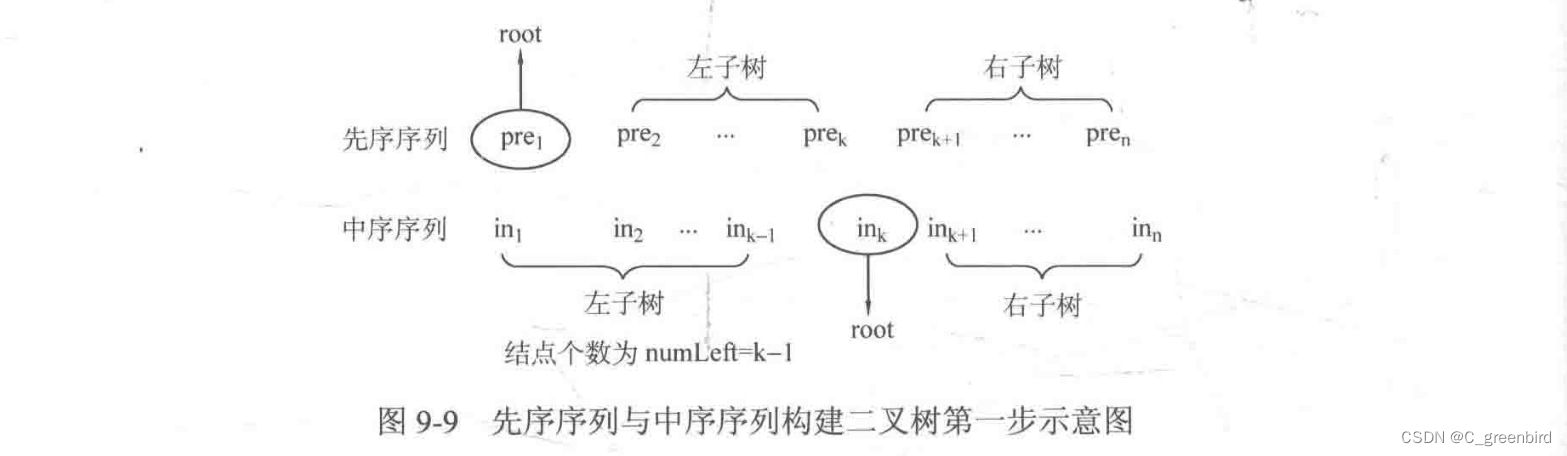
PS:图解来自胡凡《算法笔记》P294。
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
* right(right) {}
* };
*/
class Solution {
public:
TreeNode* create(vector<int>& preorder, vector<int>& inorder, int preL,
int preR, int inL, int inR) {
if (preL > preR) {
return nullptr;
}
TreeNode* root = new TreeNode(preorder[preL]);
int k;
for (k = 0; k < inorder.size(); k++) {
if (inorder[k] == preorder[preL]) {
break;
}
}
int numLeft = k - inL;
root->left =
create(preorder, inorder, preL + 1, preL + numLeft, inL, k - 1);
root->right =
create(preorder, inorder, preL + numLeft + 1, preR, k + 1, inR);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int n = preorder.size();
return create(preorder, inorder, 0, n - 1, 0, n - 1);
}
};
106 从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:
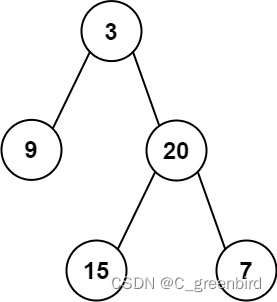
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]
提示:
1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder 和 postorder 都由 不同 的值组成
postorder 中每一个值都在 inorder 中
inorder 保证是树的中序遍历
postorder 保证是树的后序遍历
思路
和上题思路类似。只不过root为后序遍历的最后一个节点。
利用递归实现的过程,假设后序遍历数组postorder的区间为[postL,postR],中序遍历数组inorder的区间为[inL,inR]。那么中间的根节点为postorder[postR],利用k标记找到inorder中的根节点,那么
左子树节点个数为numLeft = k-inL.
左子树的后序遍历区间为[postL, postL+numLeft-1],中序遍历区间为[inL,k-1];
右子树的后序遍历区间为[postL+numLeft, postR-1],中序遍历区间为[k+1,inR].
这样一直递归下去即可。
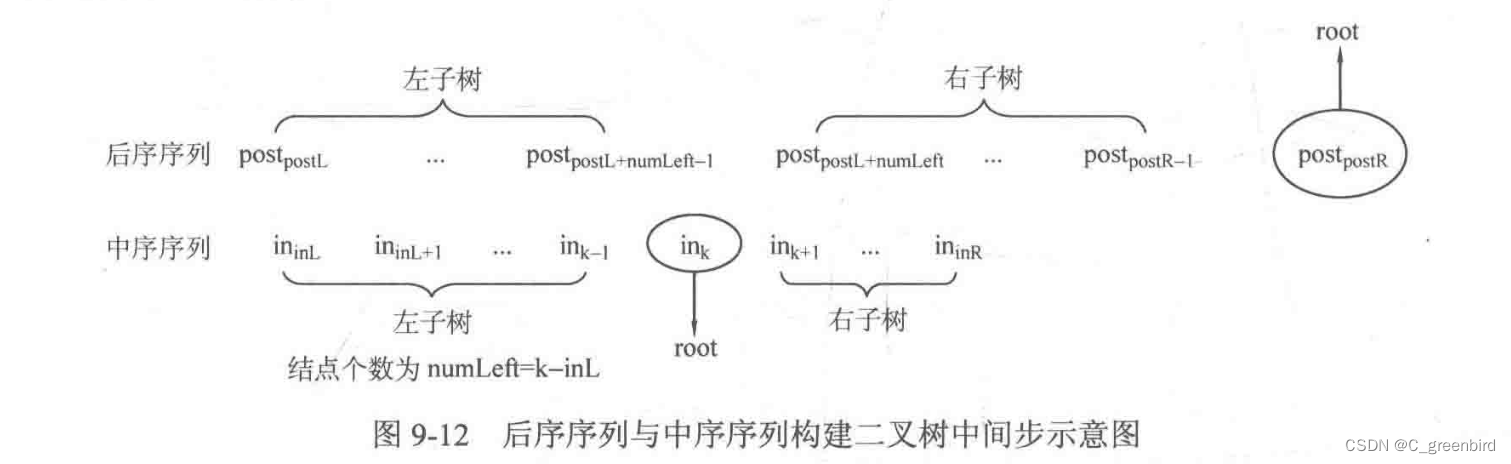
PS:图解来自胡凡《算法笔记》P296。
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
* right(right) {}
* };
*/
class Solution {
public:
TreeNode* create(vector<int>& inorder, vector<int>& postorder, int postL,
int postR, int inL, int inR) {
if (postL > postR) {
return nullptr;
}
TreeNode* root = new TreeNode(postorder[postR]);
int k;
for (k = 0; k < postorder.size(); k++) {
if (inorder[k] == postorder[postR]) {
break;
}
}
int numLeft = k - inL;
root->left =
create(inorder, postorder, postL, postL + numLeft - 1, inL, k - 1);
root->right =
create(inorder, postorder, postL + numLeft, postR - 1, k + 1, inR);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
int n = inorder.size();
return create(inorder, postorder, 0, n - 1, 0, n - 1);
}
};

![【Osek网络管理测试】[TG3_TC5]等待总线睡眠状态_1](https://img-blog.csdnimg.cn/direct/d34de03cba2144f8b3676dfc80a5bcdf.png)