项目管理：每天进步一点点~   

                  活到老，学到老  ヾ(◍°∇°◍)ﾉﾞ

                  何时学习都不晚，加油

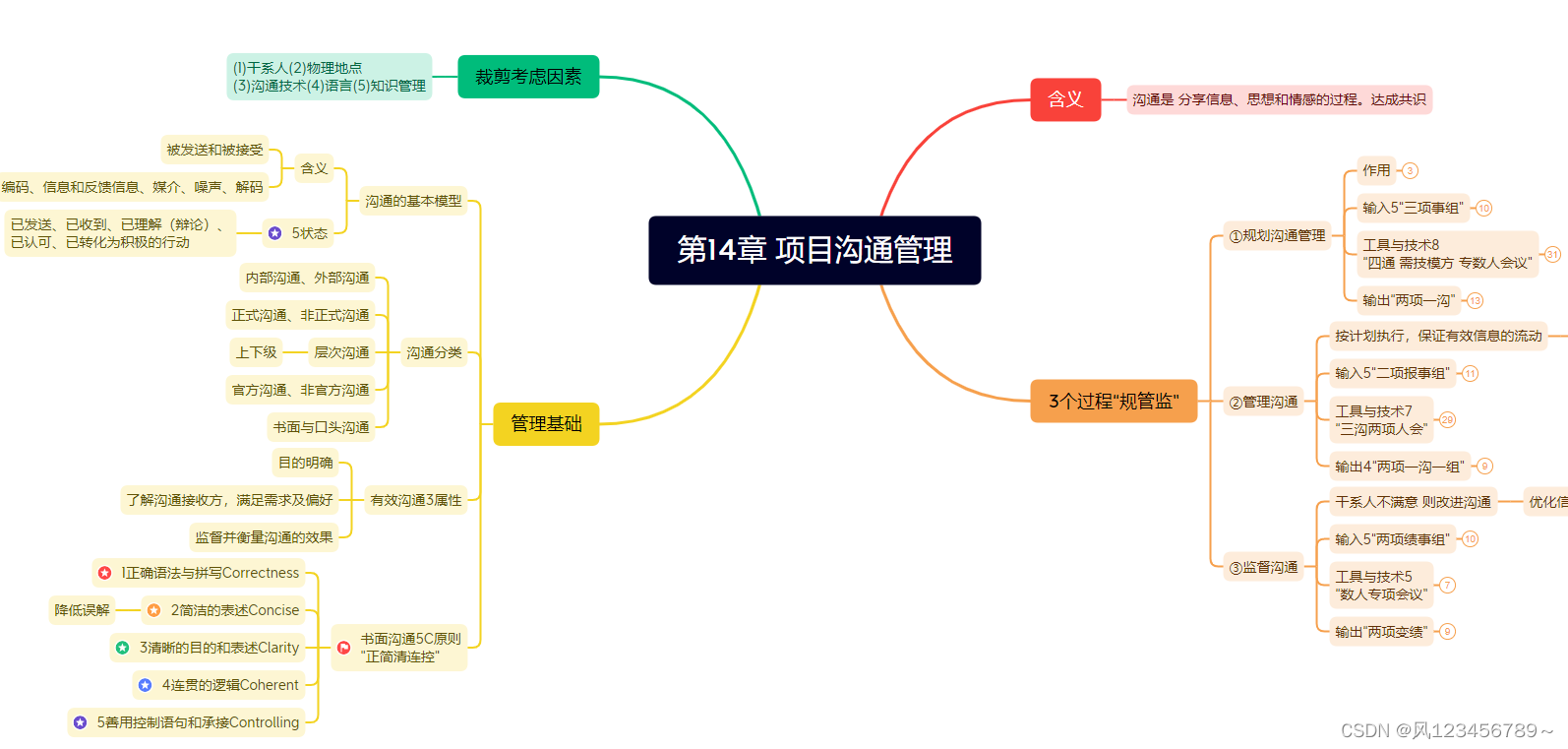
1.项目沟通管理-主要内容

项目沟通管理过程--重点：

①ITTO 输入，输出工具和技术。

②问题和解决方案。

③论文可以结合范围，进度，成本。

 书面沟通5C原则

"正简清连控"
    1正确语法与拼写Correctness
    2简洁的表述Concise-- 降低误解
    3清晰的目的和表述Clarity
    4连贯的逻辑Coherent
    5善用控制语句和承接Controlling

2.项目沟通管理-3个过程

     项目沟通管理3个过程“规管监”：规划沟通管理、管理沟通、监督沟通。

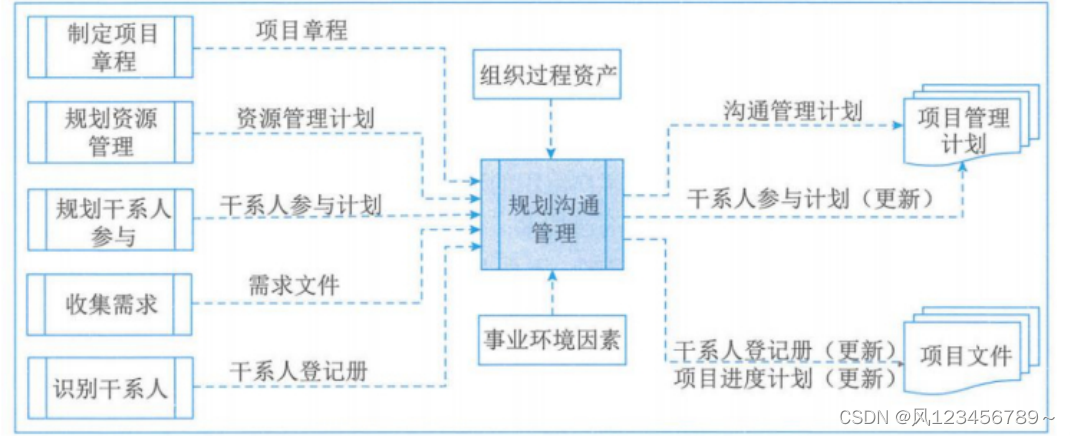
2.1规划沟通管理

（1）主要内容

（2）工具与技术

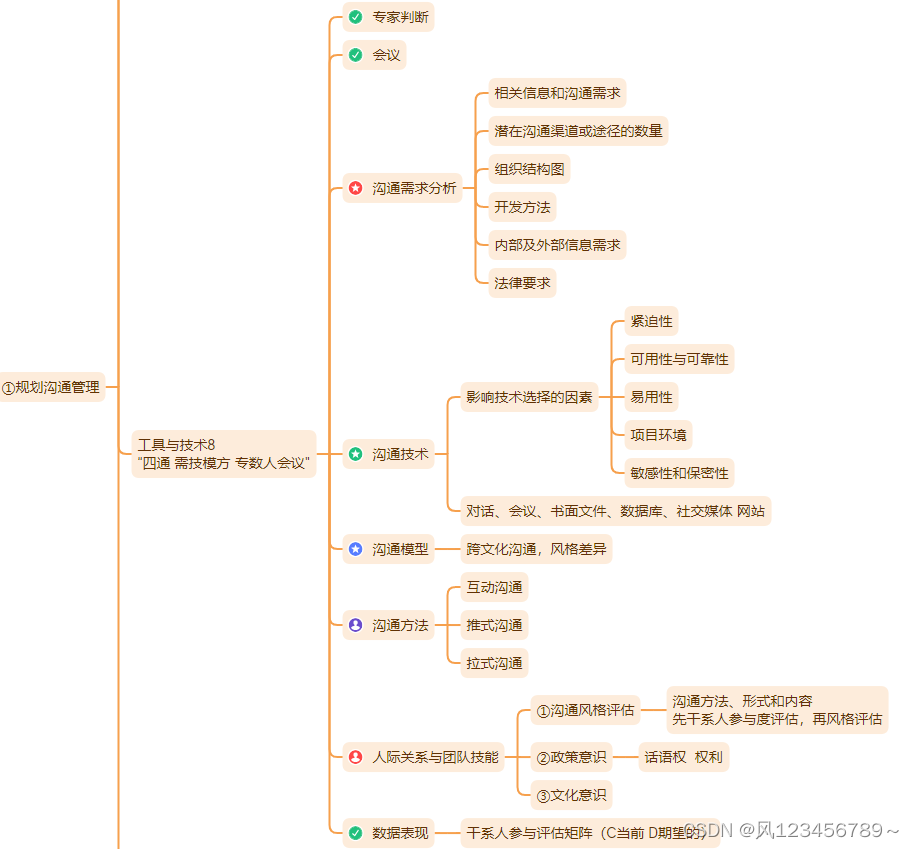
（3）数据流向

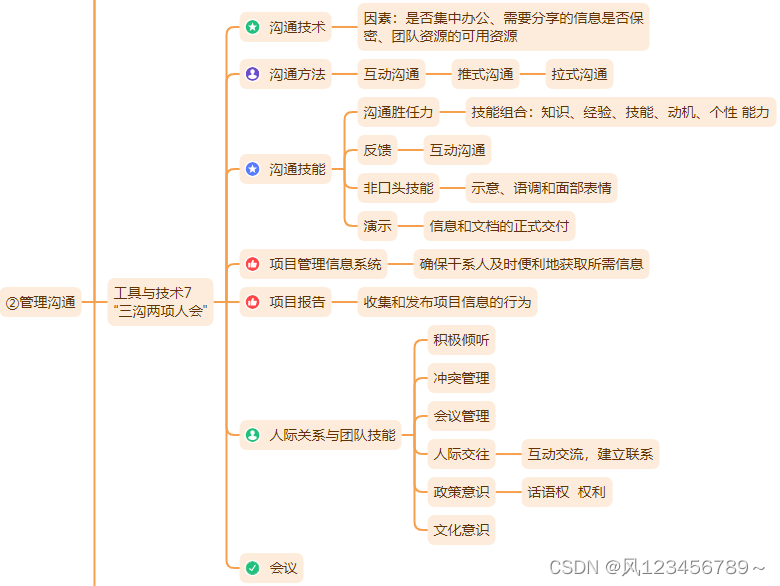
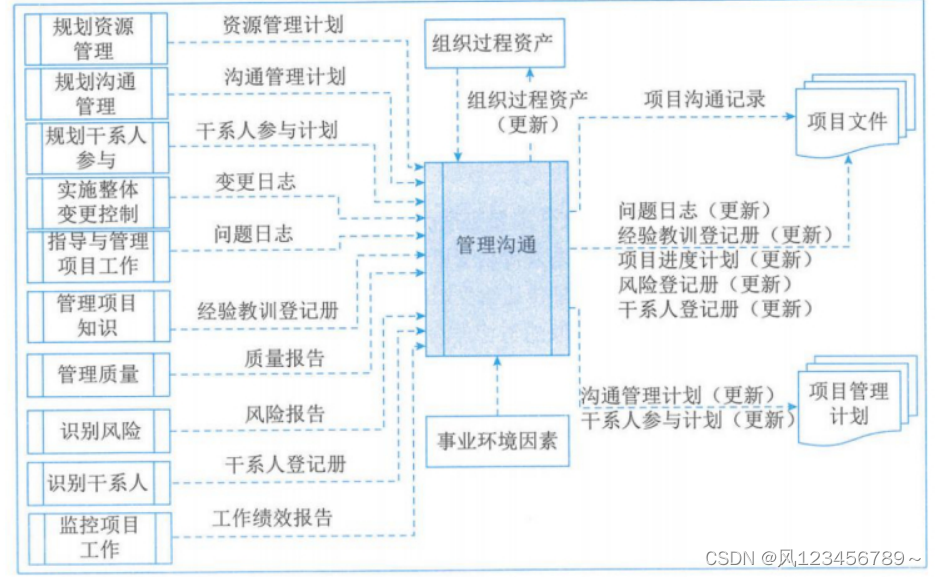
2.2管理沟通

（1）主要内容

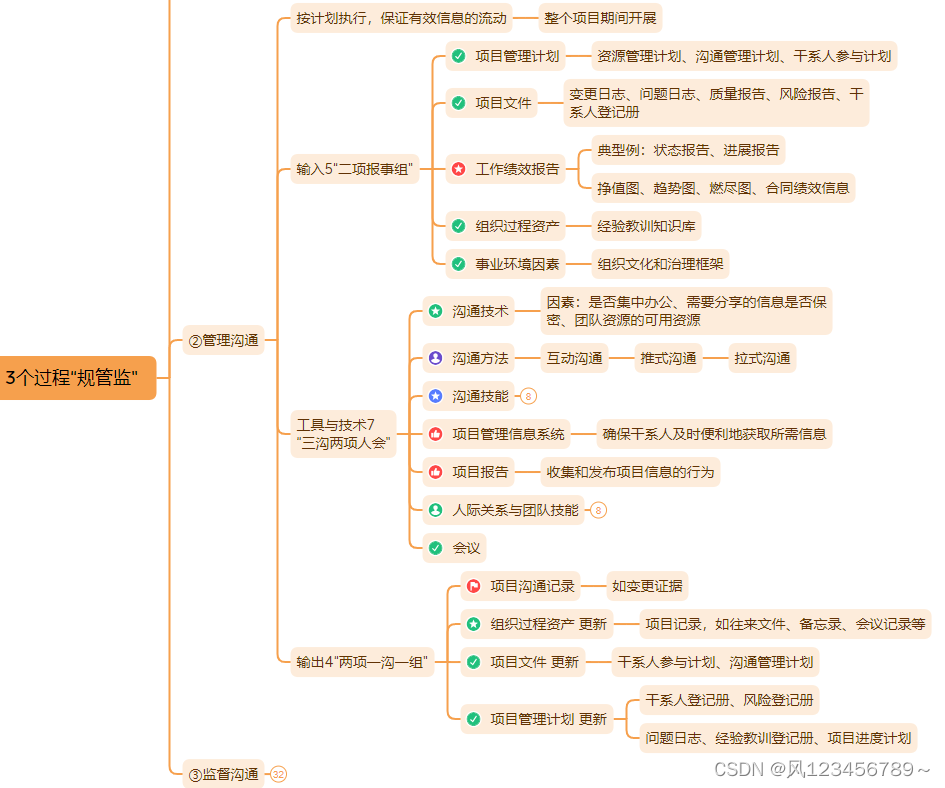
（2）工具与技术

（3）数据流向

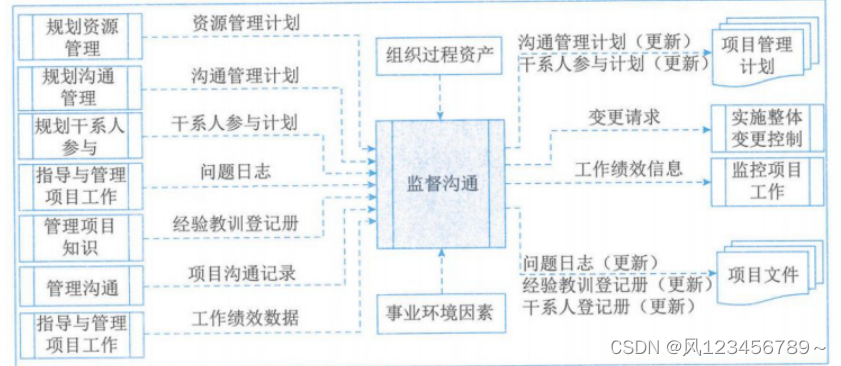
2.3监督沟通

（1）主要内容

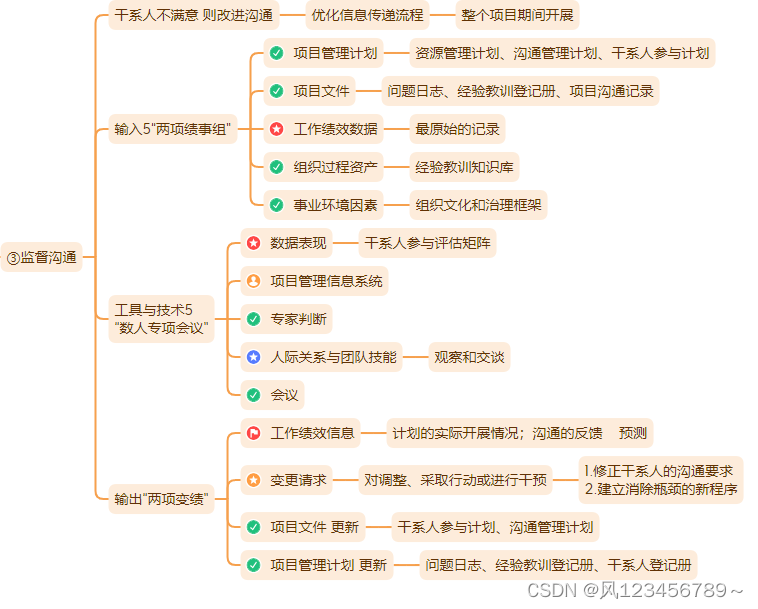
（2）数据流向