（题目来源：力扣）

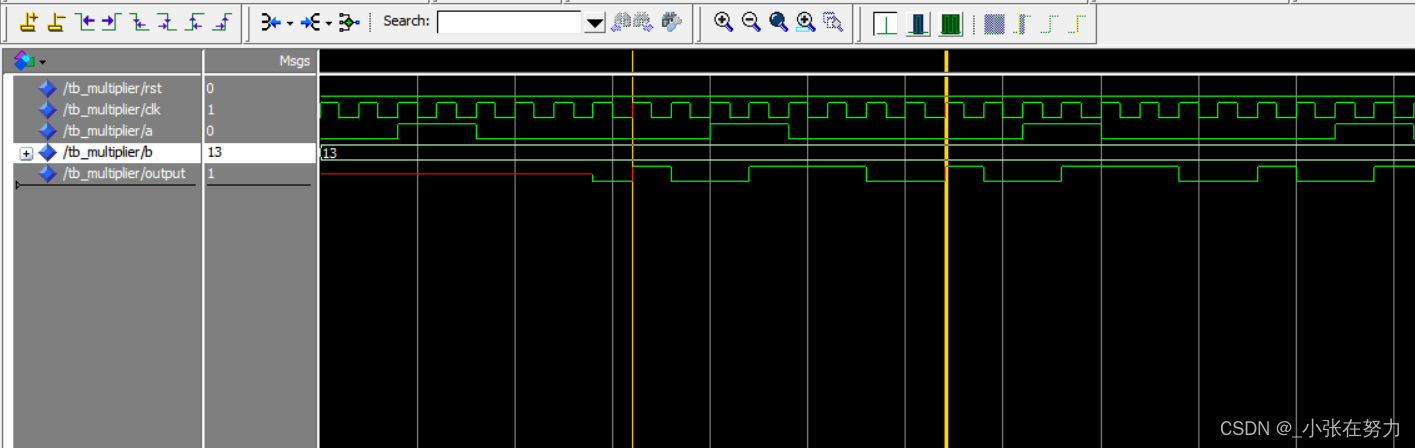
一.判读一个链表是否是环形链表

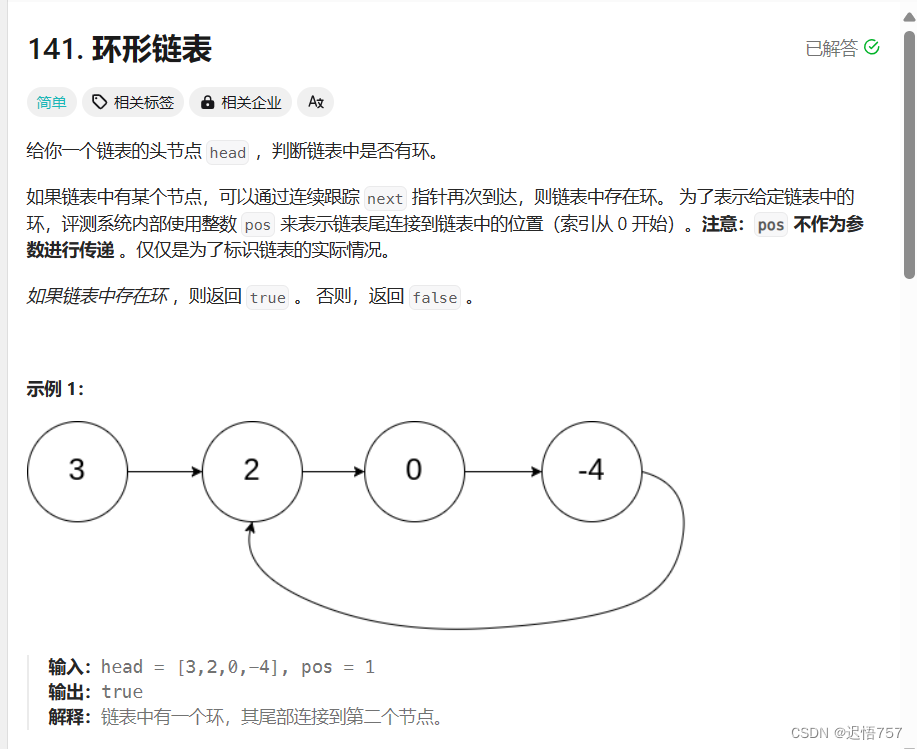
题目： 

解答：

方法：快慢指针法 

内容：分别定义快慢指针（fast和slow），快指针一次走两步，慢指针一次走一步。

原理：若不成环，则快指针(或快指针的next）一定会走到空，据此，写出循环条件，当循环结束时，返回NULL

while(fast&&fast->next)

此时，问题来了，成环怎么办？不能再通过循环条件来判断（因为此时该循环是死循环了）

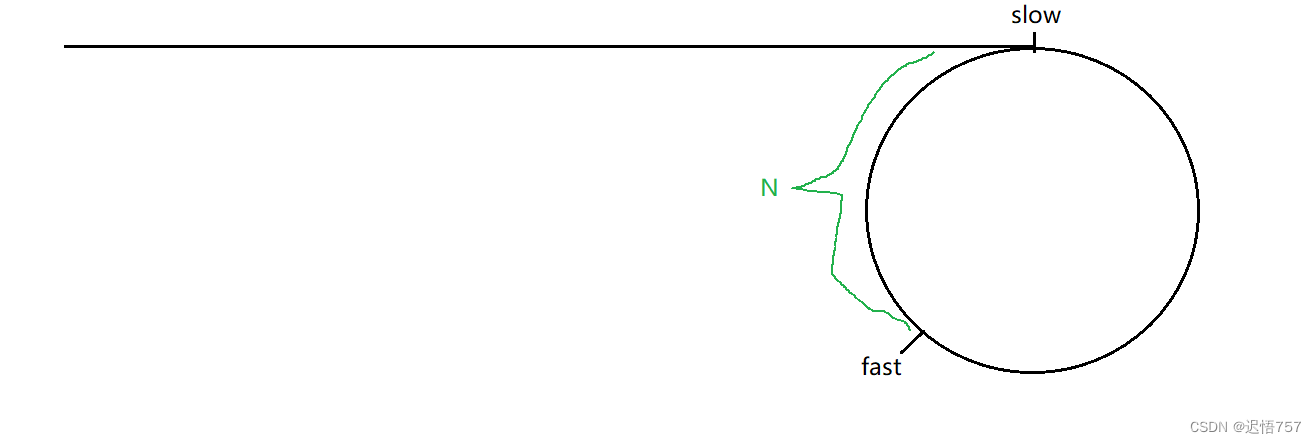
目光再回到快慢指针上，若成环，则快指针一定会有追上慢指针的时候，当它们相遇时，循环结束

证明：

当fast，slow都进入环时：
假设：fast，slow之间相距N（单位：节点）
fast一次走两步，slow一次走一步，则每走一次，二者之间的距离就减1
如此循环往复，距离一定会变为0，即一定相遇

 解题代码（并非完整代码）

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
bool hasCycle(struct ListNode *head) 
{
    struct ListNode* fast = head;
    struct ListNode* slow = head;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(fast == slow)
        {
            return true;
        }
    }
    return false; 
}

拓展：

fast走3步可以吗？n步呢？

当fast一次走3步时：
假设：fast，slow之间相距N（单位：节点）
fast一次走三步，slow一次走一步，则每走一次，二者之间的距离就减2，变为N-2
情况1：N为偶数，则距离一定会变为0，即相遇

情况2：N为奇数

则距离会逐渐递减为-1（N-2,N-4,...3,2,-1）（这里的-1是指fast领先slow指针一步）

fast和slow错过

假设环的总长度为C，那么fast，slow间的距离就变为C-1，继续分类讨论

情况2.1：C-1为偶数，则一定会相遇

情况2.2：C-1为奇数，则二者之间的距离最终又会变为-1，一直错过无法相遇

 总结：当N为奇数，C为偶数时，二者一直错过，无法相遇

真的是这样吗？

C是偶数且N是奇数，这个条件能同时满足吗？

不妨推导一下： 

假设：slow 走过的路程为L，当slow进入环时，fast已经绕环走了x (x>=0) 圈，环的长度为C

（slow 走过的路程简记为slow，fast同理）

slow = L 

fast = L + x*C + C-N

3*slow = fast

则 3*L = L + x*C + C-N

化简得 N =（x+1）* C - 2*L

C是偶数，2*L也是偶数，N一定是偶数，不可能是奇数，所以此条件不可能同时成立，fast与slow一定会相遇

（fast走n步的情况就交给读者自行思考了）

二.找到环形链表开始进入环的第一个节点

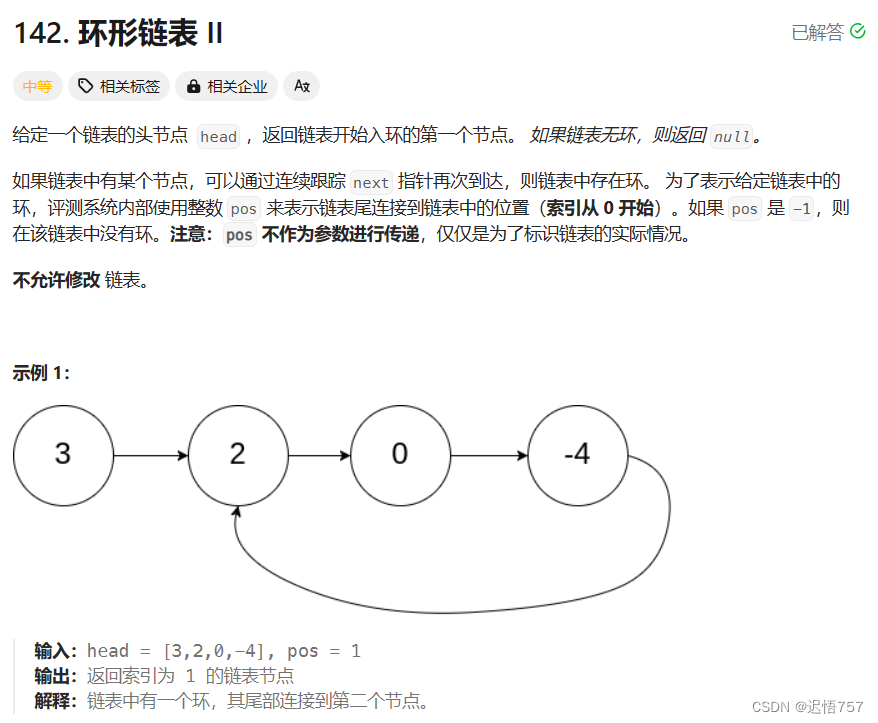
题目： 

解答:

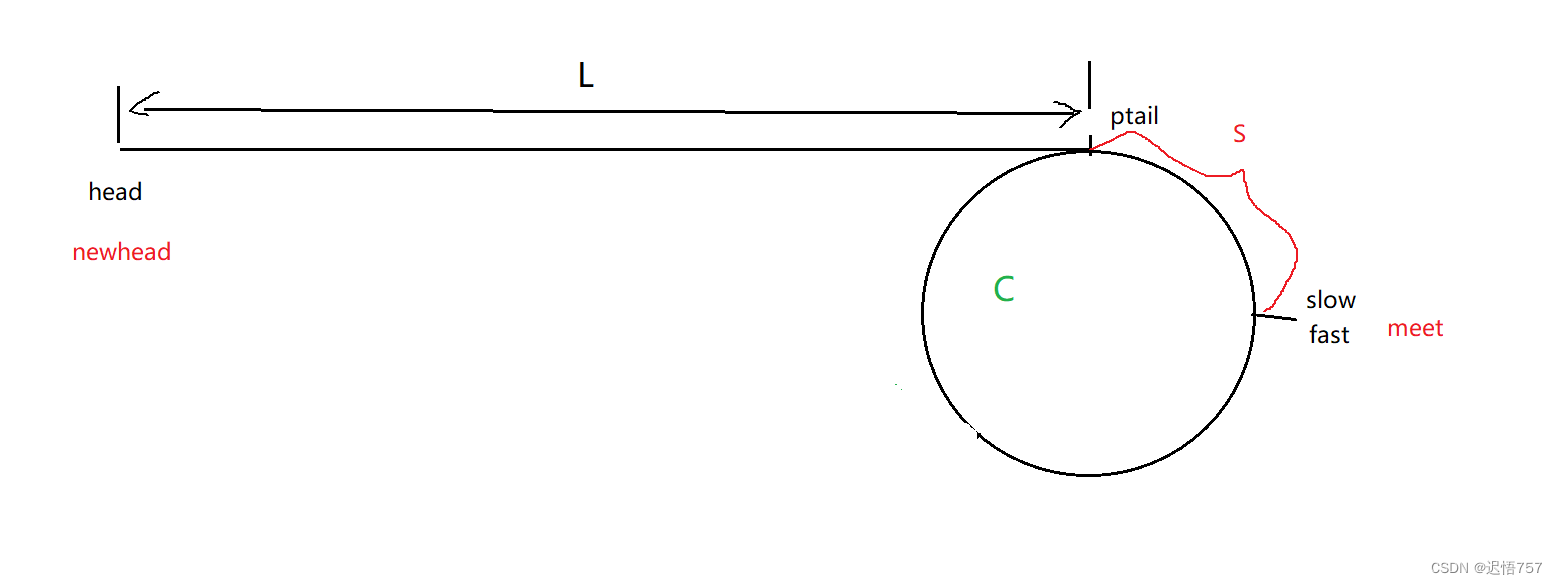
设进入环的第一个节点为 ptail

1.先判断是否是环形链表（同上）

2.找到开始进入环的第一个节点

方法：

先定义快慢指针：fast和slow，fast一次走两步，slow一次走一步

先让fast和slow相遇，定义meet指针指向相遇节点

定义一个新指针newhead 指向链表的头结点，然后让newhead和meet指针同时向前走，他们相遇的节点就是ptail

证明：

假设：slow 走过的路程为L + S(L是环外走过的路程，S是环内走过的路程），相遇时，fast已经绕环走了x圈（x>=1），环的长度为C

（slow 走过的路程简记为slow，fast同理）

（补充：slow和fast相遇时，S一定小于C，因为slow走完一圈之前，二者一定会相遇）

slow = L + S

fast = L + x*C + S

2*slow = fast

2*（L + S）=  L + x*C + S

L  = x*C - S = （x-1）* C + C - S

L 是newhead到ptail间的距离，（x-1）* C是环长度的整数倍，C - S是meet到ptai的距离

所以当newhead和meet一定相遇在ptail节点

证毕

解题代码(非完整代码）

struct ListNode *detectCycle(struct ListNode *head) 
{
    //先判断有无环，并找到相遇时的节点
    struct ListNode* fast = head;
    struct ListNode* slow = head;
    struct ListNode* meet = NULL;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        //相遇
        if(fast == slow)
        {
            meet = fast;
            struct ListNode* newhead = head;
            while(newhead != meet)
            {
            newhead = newhead->next;
            meet = meet->next;
            }
            return meet;
        }
    }
    return NULL;
}