【莫比乌斯变换-04】求解莫比乌斯变换系数

求解莫比乌斯变换系数

在这里插入图片描述

文章目录

一、说明
二、如何确定双线性变换系数
- 2.1 变换基本形式
- 2.2 通过三点确定
三、一般情况的变换
- 3.1 最简单的情况：无穷大
- 3.2 处理无穷大
四、Python 代码

一、说明

上一篇文章是对双线性变换的视觉介绍，又名莫比乌斯变换或分数线性变换。这篇文章是一个简短的后续文章，更多地关注如何计算变换的系数。

二、如何确定双线性变换系数

2.1 变换基本形式

双线性变换（莫比乌斯变换） f 的形式为：

$\frac{az + b}{cz + d}$

其中 $A D - BC \neq = 0$ 。

逆变换，f 的倒数由下式给出

$\frac{dw - b}{-cw + a}$

变换 f 在除 z = –d/c 之外的任何地方都定义，其逆变换在除 w = a/c 之外的任何地方都定义。

所以 f 将复平面减去 1 点到复平面减去 1 点。或者一种优雅的思考方式是通过在无穷远处添加一个点来将 f 和 g 视为球体上的函数。然后我们说

$\begin{align*} f（-d/c） &= \infty \\ g（\infty） &= -d/c \\ f（\infty） = a/c \\ g（a/c） &= \infty \end{align*}$

2.2 通过三点确定

双线性变换有三个自由度。也就是说，您可以在域中选取三个值，并为它们在范围内指定三个位置。唯一的双线性变换发送 z1、z2和 z3至 W1、w2和 w3由下式给出

$\frac{（w - w_2）（w_3 - w_1）}{（w - w_1）（w_3 - w_2）} = \frac{（z - z_2）（z_3 - z_1）}{（z - z_1）（z_3 - z_2）}$

代入常量并求解 w = f（z）。

更新：以下是系数的显式公式。
例如，让我们看一下上一篇文章中的笑脸示例。

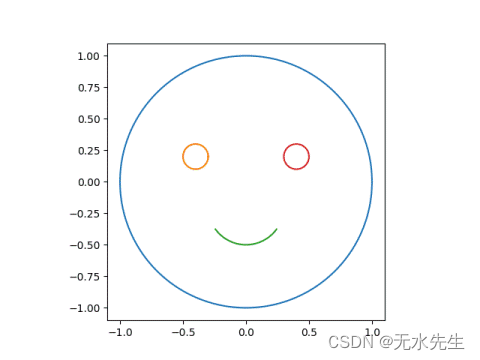
在这里插入图片描述

我们会在脸上选择三个点和三个地方让他们去。
假设我们希望脸部的中心保持原位，将 0 映射到 0。接下来，让我们选择两个眼睛中心的位置。这些在±0.4+.2ji。假设我们希望左眼下降一点到 -0.4，右眼上升一点到 0.5 + 0.3i。

我使用 Mathematica 求解参数。

{z1, z2, z3} = {0, -2/5 + I/5, 2/5 + I/5}
{w1, w2, w3} = {0, -2/5, 1/2 + 3 I/10}
Solve[(w - w2) (w3 - w1)/((w - w1) (w3 - w2)) == 
      (z - z2) (z3 - z1)/((z - z1) (z3 - z2)), w]

这表示参数在 Python 表示法中是，

a = -72 - 16j
b = 0
c = 30 - 35j
d = -75

使用上一篇文章中的代码，我们可以验证此转换是否执行了我们设计它的功能。

print(mobius(0, a, b, c, d))
print(mobius(-0.4 + 0.2j, a, b, c, d))
print(mobius(0.4 + 0.2j, a, b, c, d))

我们可以看看结果。
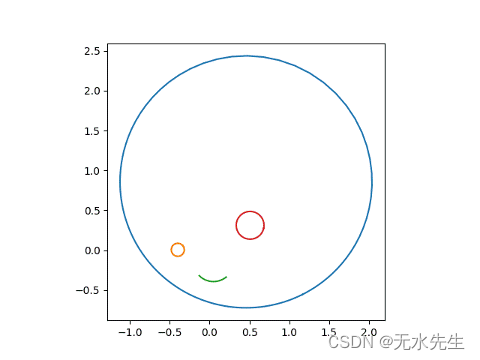
在这里插入图片描述

三、一般情况的变换

上文说明，莫比乌斯变换由其在三个点上的值唯一决定。通过这个信息确定莫比乌斯变换的系数。我说上面计算不失为一个方法，但仍有一些工作要做。在特定情况下，找到系数并不难，但一般来说要找到系数会更难。

给定指定的点 z 的每个参数 a、b、c 和 d 都有一个显式公式1、z2、z3和他们的图像 w1、w2、w3我们稍后将介绍。我们可以很容易地对这些公式进行编码，但有一个复杂因素除外：我们可能希望我们的一个输入，我们的输出是∞的。这不仅仅是一个极端情况：在应用中，例如信号处理，您通常希望指定极点的位置。

3.1 最简单的情况：无穷大

如果输入或输出都不是无限的，则系数由下式给出

$\begin{align*} a &= \begin{vmatrix} z_1w_1 & w_1 & 1 \\ z_2w_2 & w_2 & 1 \\ z_3w_3 & w_3 & 1 \end{vmatrix} \\ b &= \begin{vmatrix} z_1w_1 & z_1 & w_1 \\ z_2w_2 & z_2 & w_2 \\ z_3w_3 & z_3 & w_3 \end{vmatrix} \\ c &= \begin{vmatrix} z_1\phantom{w_1} &w_1 & 1 \\ z_2\phantom{w_1} & w_2 & 1 \\ z_3\phantom{w_1} & w_3 & 1 \end{vmatrix} \\ d &= \begin{vmatrix} z_1w_1 & z_1 & 1 \\ z_2w_2 & z_2 & 1 \\ z_3w_3 & z_3 & 1 \end{vmatrix} \end{align*}$

这是一种解决方案;将所有四个系数乘以一个非零常数可以得到另一个解决方案。但是模常数，解是唯一的。换句话说，莫比乌斯变换是唯一的，但它的表示只有在分子和分母相乘的常数之前是唯一的。

你可能会希望这个公式会起作用，如果你只是让浮点无穷大自己照顾好自己。但是，如果 z 或 w 中的任何一个是无限的，那么上面的每个行列式都是无限的。

3.2 处理无穷大

无穷大的可能情况是：

无穷大
只有一个 z 是无限的
只有一个 w 是无限的
具有相同下标的 z 和 w 是无限的
具有不同下标的 z 和 w 是无限的
我们的 z 和 w 的顺序是任意的，因此为了方便起见，我们可以在必要时重新排列它们。因此，在不失去普遍性的情况下，我们可以假设
无穷大
只有 z1是无限的
只有 w1是无限的
z1 = w1= ∞
z1 = w2= ∞
处理 z 的情况（2）1= ∞，将上面的每个方程除以 z1并将极限设为 z1接近∞。由于矩阵的一行除以一个常数将其行列式除以相同的量，因此在每种情况下，我们将第一行除以 z1.这效果很好，因为 z1只出现在每个矩阵的第一行中。我们可以处理 2 个案例（3）1= ∞ 类似。

处理 z 的情况（4）1 = w1= ∞我们将第一行除以 z1 w1并采取限制。处理 z 的情况（5）1 = w2= ∞我们将第一行除以 z1第二行由 W1并采取限制。

如果你觉得这个限制性业务是可疑的，那也没关系：如果结果是正确的，它就是正确的。由于莫比乌斯变换是由它们在三个点上的值决定的，因此您可以通过坚持 z 来验证每种情况是否正确1、z2、z3并检查你是否得到 W1、w2、w3外。您可以手动执行此操作，我有，或者信任帖子底部的代码输出。

因此，这是我们的解决方案。

（1）无无限
如上所述。
（2）只有 z1= ∞
一个 = W1 (w2– W3)
b = w1 (z2 w3– z3 w2) + w2 w3 (z3– z2)
c = w2– W3
d = w1 (z2– z3)– z2w2 + z3 w3
（3）只有 w1= ∞
a = z1 (w2– W3)– z2w2+ Z3 w3
b = z1 (z2 w3– z3 w2) + z2 z3 (w2– W3)
c = z3– z2
d = z1 (z2– z3)

注意：你可以从案例 z 中推导出这些1= ∞ 通过反转转换。这意味着将 z 与 w 交换，将 a 和 d 交换，并否定 b 和 c。

（4） z1 = w1= ∞
一个 = W2– W3
b = z2 w3– z3 w2
c = 0
d = z2– z3
（5） Z1 = w2= ∞
一个 = W1
b = –z2 w3 + z3 (w3– W1)
c = 1
d = –z2

四、Python 代码

import numpy as np

def all_finite(z1, z2, z3, w1, w2, w3):
    a = np.linalg.det(
            [[z1*w1, w1, 1],
             [z2*w2, w2, 1],
             [z3*w3, w3, 1]])
    b = np.linalg.det(
            [[z1*w1, z1, w1],
             [z2*w2, z2, w2],
             [z3*w3, z3, w3]])
    c = np.linalg.det(
            [[z1, w1, 1],
             [z2, w2, 1],
             [z3, w3, 1]])
    d = np.linalg.det(
            [[z1*w1, z1, 1],
             [z2*w2, z2, 1],
             [z3*w3, z3, 1]])
    return (a, b, c, d)

def z1_infinite(z1, z2, z3, w1, w2, w3):
    assert(np.isinf(z1))
    a = w1*(w2 - w3)
    b = w1*(z2*w3 - z3*w2) + w2*w3*(z3 - z2)
    c = w2 - w3
    d = w1*(z2 - z3) - z2*w2 + z3*w3
    return (a, b, c, d)    

def w1_infinite(z1, z2, z3, w1, w2, w3):
    assert(np.isinf(w1))
    a = z1*(w2 - w3) - z2*w2 + z3*w3
    b = z1*(z2*w3 - z3*w2) + z2*z3*(w2 - w3)
    c = z3 - z2
    d = z1*(z2 - z3)
    return (a, b, c, d)        

def z1w1_infinite(z1, z2, z3, w1, w2, w3):
    assert(np.isinf(z1) and np.isinf(w1))
    a = w2 - w3
    b = z2*w3 - z3*w2
    c = 0
    d = z2 - z3
    return (a, b, c, d)            

def z1w2_infinite(z1, z2, z3, w1, w2, w3):
    assert(np.isinf(z1) and np.isinf(w2))
    a = w1
    b = -z2*w3 + z3*(w3 - w1)
    c = 1
    d = -z2
    return (a, b, c, d)                

def mobius_coeff(z1, z2, z3, w1, w2, w3):

    infz = np.isinf(z1) or np.isinf(z2) or np.isinf(z3)
    infw = np.isinf(w1) or np.isinf(w2) or np.isinf(w3)    

    if infz:
        if np.isinf(z2):
            z1, z2 = z2, z1
            w1, w2 = w2, w1
        if np.isinf(z3):
            z1, z3 = z3, z1
            w1, w3 = w3, w1
        if infw:
            if np.isinf(w1):
                return z1w1_infinite(z1, z2, z3, w1, w2, w3)
            if np.isinf(w3):
                z2, z3 = z3, z2
                w2, w3 = w3, w2
            return z1w2_infinite(z1, z2, z3, w1, w2, w3)
        else:
            return z1_infinite(z1, z2, z3, w1, w2, w3)
        
    if infw: # and all z finite
        if np.isinf(w2):
            z1, z2 = z2, z1
            w1, w2 = w2, w1
        if np.isinf(w3):
            z1, z3 = z3, z1
            w1, w3 = w3, w1
        return w1_infinite(z1, z2, z3, w1, w2, w3)

    return all_finite(z1, z2, z3, w1, w2, w3)

def mobius(x, a, b, c, d):
    if np.isinf(x):
        if c == 0:
            return np.inf
        return a/c
    if c*x + d == 0:
        return np.inf
    else:
        return (a*x + b)/(c*x + d)
    
def test_mobius(z1, z2, z3, w1, w2, w3):
    tolerance = 1e-6
    a, b, c, d = mobius_coeff(z1, z2, z3, w1, w2, w3)
    for (x, y) in [(z1, w1), (z2, w2), (z3, w3)]:
        m = mobius(x, a, b, c, d)
        assert(np.isinf(m) and np.isinf(y) or abs(m - y) <= tolerance)

test_mobius(1, 2, 3, 6, 4, 2)
test_mobius(1, 2j, 3+7j, 6j, -4, 2) 
test_mobius(np.inf, 2, 3, 8j, -2, 0)
test_mobius(0, np.inf, 2, 3, 8j, -2)
test_mobius(0, -1, np.inf, 2, 8j, -2)
test_mobius(1, 2, 3, np.inf, 44j, 0)
test_mobius(1, 2, 3, 1, np.inf, 40j)
test_mobius(-1, 0, 3j, 1, -1j, np.inf)
test_mobius(np.inf, -1j, 5, np.inf, 2, 8)
test_mobius(1, np.inf, -1j, 5, np.inf, 2)
test_mobius(12, 0, np.inf, -1j, 5, np.inf)
test_mobius(np.inf, -1j, 5, 0, np.inf, -1)
test_mobius(6, np.inf, -1j, 0, 8, np.inf)
test_mobius(6, 3j, np.inf, -1j, np.inf, 1)