1.数据集准备

下载数据集 

https://download.openmmlab.com/mmocr/data/wildreceipt.tar

WildReceiptOpenset

• 准备好 WildReceipt。

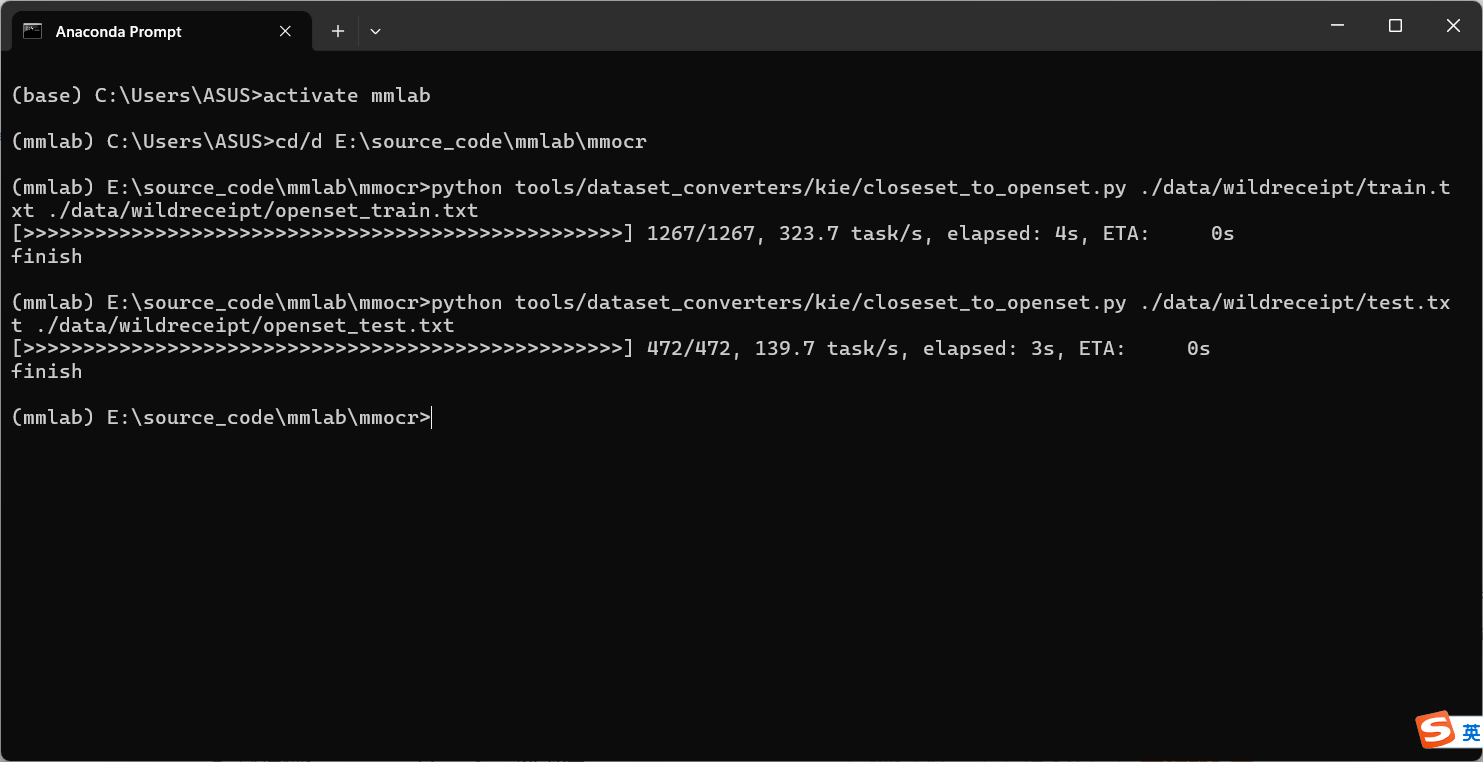
• 转换 WildReceipt 成 OpenSet 格式:

# 你可以运行以下命令以获取更多可用参数：
# python tools/dataset_converters/kie/closeset_to_openset.py -h
python tools/dataset_converters/kie/closeset_to_openset.py ./data/wildreceipt/train.txt ./data/wildreceipt/openset_train.txt
python tools/dataset_converters/kie/closeset_to_openset.py ./data/wildreceipt/test.txt ./data/wildreceipt/openset_test.txt

2.修改配置文件

修改数据路径为自己的路径