0. 统一入口

设置一个统一的排序操作接口。

template <typename T>
void List<T>::sort ( ListNodePosi(T) p, int n ) { //列表区间排序
	switch ( rand() % 3 ) { //随机选择排序算法。可根据具体问题的特点灵活选择或扩充
		case 1: insertionSort ( p, n ); break; //插入排序
		case 2: selectionSort ( p, n ); break; //选择排序
		default: mergeSort ( p, n ); break; //归并排序
	}
}

1. 选择排序

1.1 构思

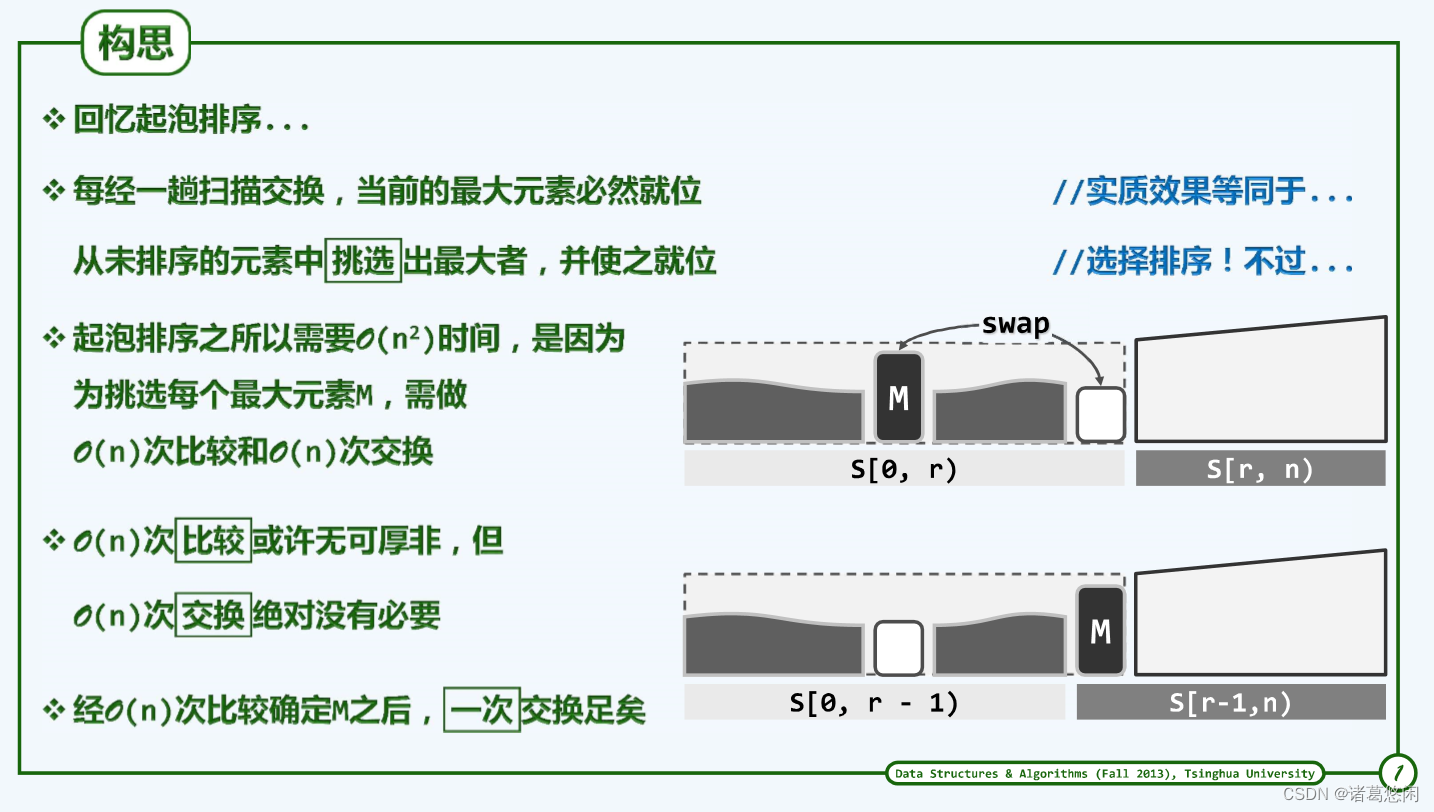
在任何时刻，后缀S[r, n)已经有序，且不小于前缀S[0, r)

起泡排序需要O($n^2$)时间，因为挑选每个最大元素M，需做O（n）次比较和O（n）次交换。

1.2 实例

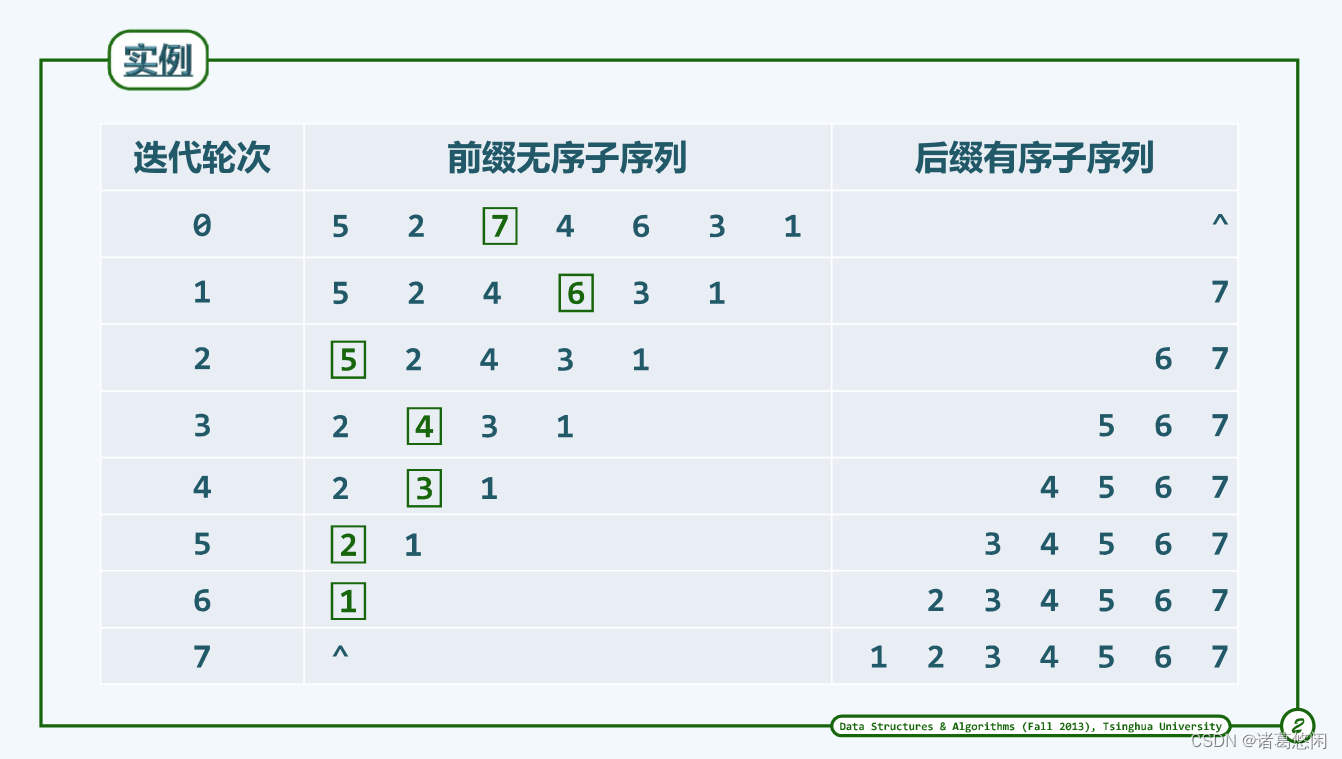
1.3 实现

算法思想：
算法迭代过程如图所示，已排序区间S[T，p+n)，未排序区间U[p,T)。在未排序区间使用selectMax()接口定位最大节点，放入已排序区间。

template <typename T> //对列表中起始于位置p、宽度为n的区间做选择排序
void List<T>::selectionSort( ListNodePosi<T> p, Rank n ) { // valid(p) && Rank(p) + n <= size
   ListNodePosi<T> head = p->pred, tail = p;
   for ( Rank i = 0; i < n; i++ ) tail = tail->succ; //待排序区间为(head, tail)
   while ( 1 < n ) { //在至少还剩两个节点之前，在待排序区间内
      ListNodePosi<T> max = selectMax ( head->succ, n ); //找出最大者（歧义时后者优先）
      insert( remove( max ), tail ); //将其移至无序区间末尾（作为有序区间新的首元素）
      tail = tail->pred; n--;
   }
}

推敲：selectionSort() 算法中insert()和remove()反复new 和delete操作，此操作虽然视为常数复杂度但时间消耗时间大概为基本操作的100倍。

优化思路：

1. 只通过对M和T两处局部引用的修改来实现同样的功能。
2. 只需交换M和T前驱节点的数据域。
   

template <typename T> //从起始于位置p的n个元素中选出最大者
ListNodePosi<T> List<T>::selectMax( ListNodePosi<T> p, Rank n ) {
   ListNodePosi<T> max = p; //最大者暂定为首节点p
   for ( ListNodePosi<T> cur = p; 1 < n; n-- ) //从首节点p出发，将后续节点逐一与max比较
      if ( !lt( ( cur = cur->succ )->data, max->data ) ) //若当前元素不小于max，则
         max = cur; //更新最大元素位置记录
   return max; //返回最大节点位置
}

插入和删除算法见列表02——无序列表。

lt 为 ”≥“ ，遇到重复元素时，返回秩最大者，保证算法的稳定性。

1.4 复杂度

θ($n^2$)的效率应有很大的改进空间。

2. 插入排序

2.1 构思

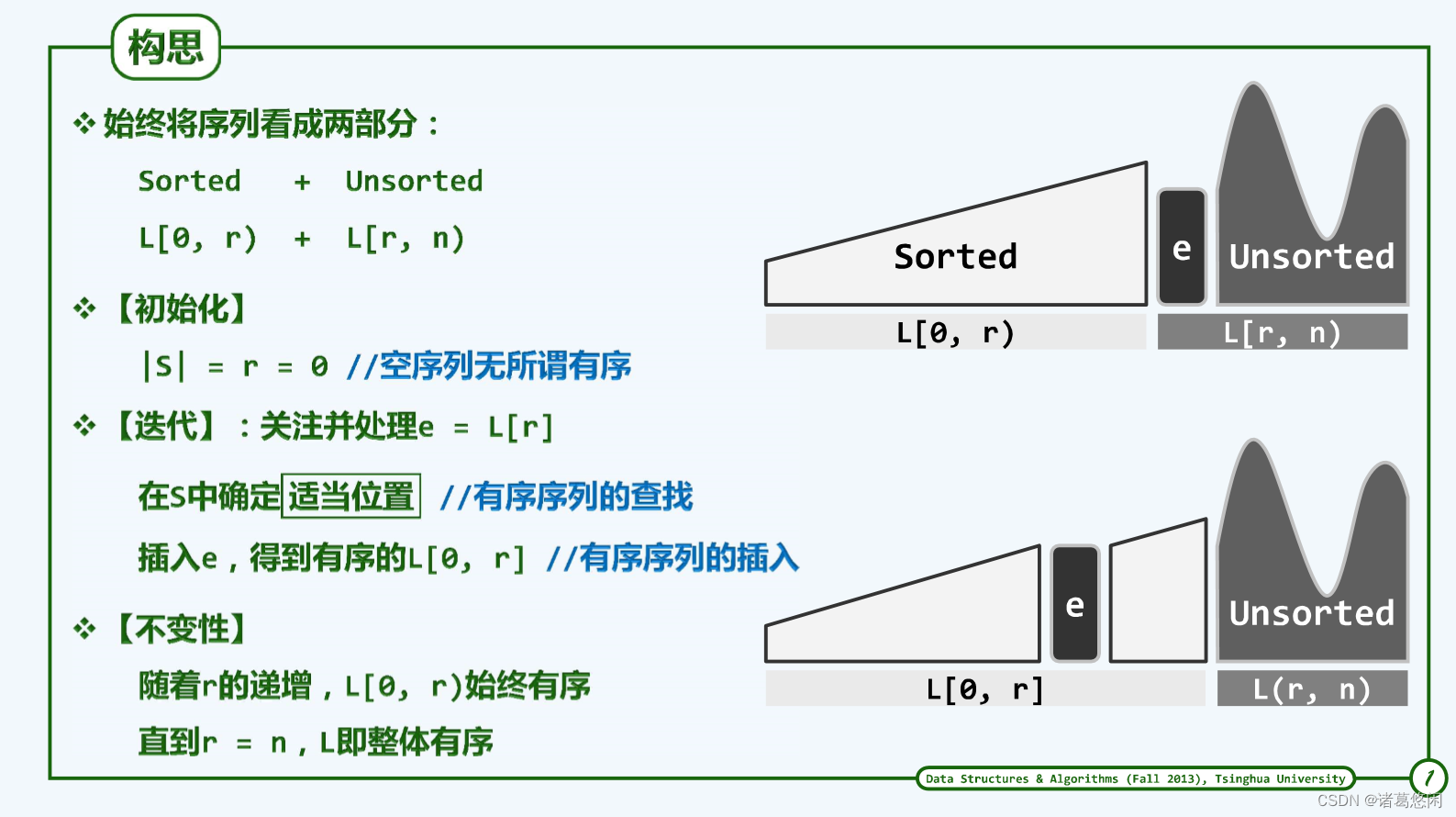
2.2 实例

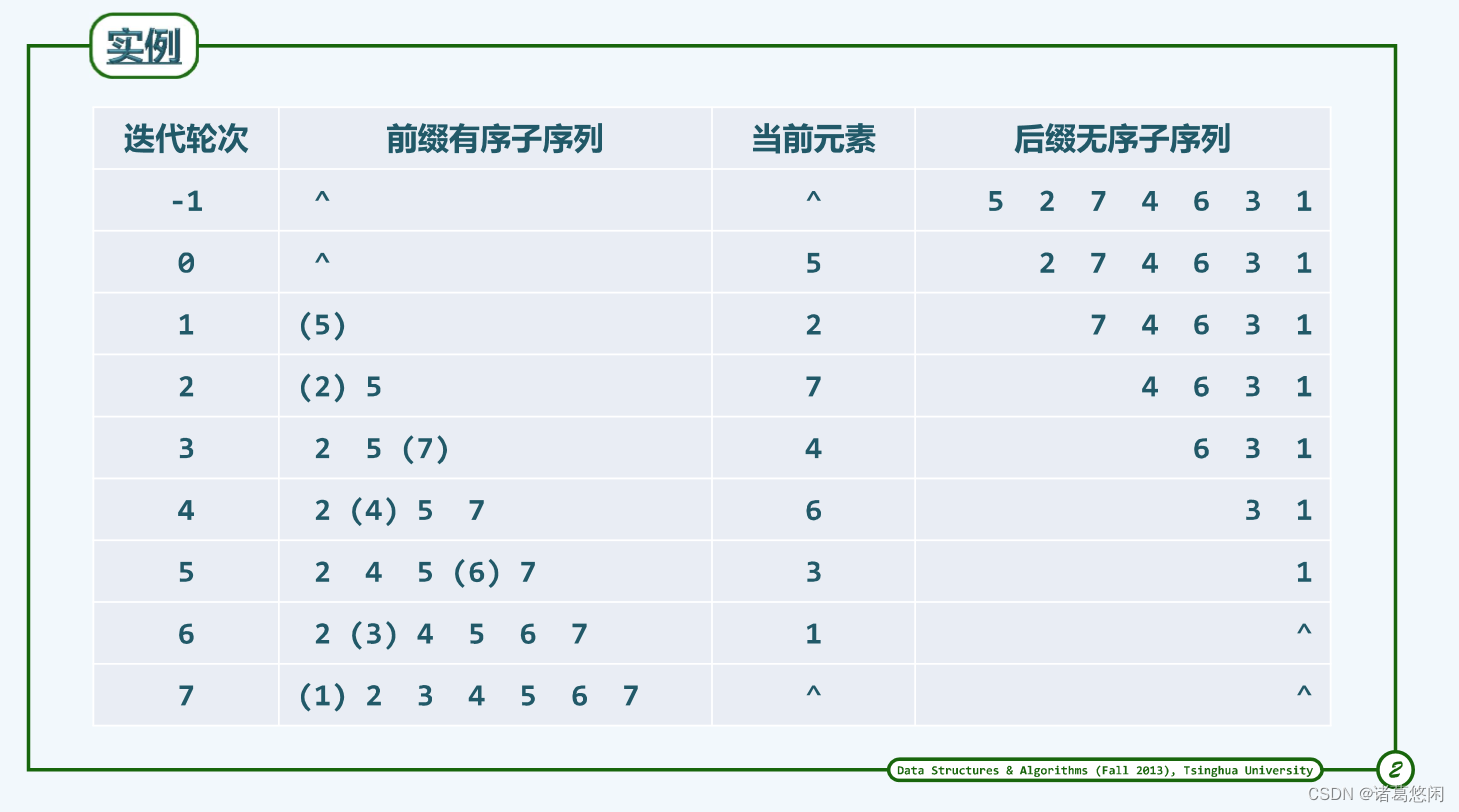
2.3 实现

算法思想：前缀S[0, r)已经有序。接下来，借助有序序列的查找算法，可在该前缀中定位到不大于e的最大元素。于是只需将e从无序后缀中取出，并紧邻于查找返回的位置之后插入，使得有序前缀的范围扩大至S[0, r]。

template <typename T> //对列表中起始于位置p、宽度为n的区间做插入排序
void List<T>::insertionSort( ListNodePosi<T> p, Rank n ) { // valid(p) && Rank(p) + n <= size
   for ( Rank r = 0; r < n; r++ ) { //逐一为各节点
      insert( search( p->data, r, p ), p->data ); //查找适当的位置并插入
      p = p->succ; remove( p->pred ); //转向下一节点
   }
}

2.4 复杂度分析

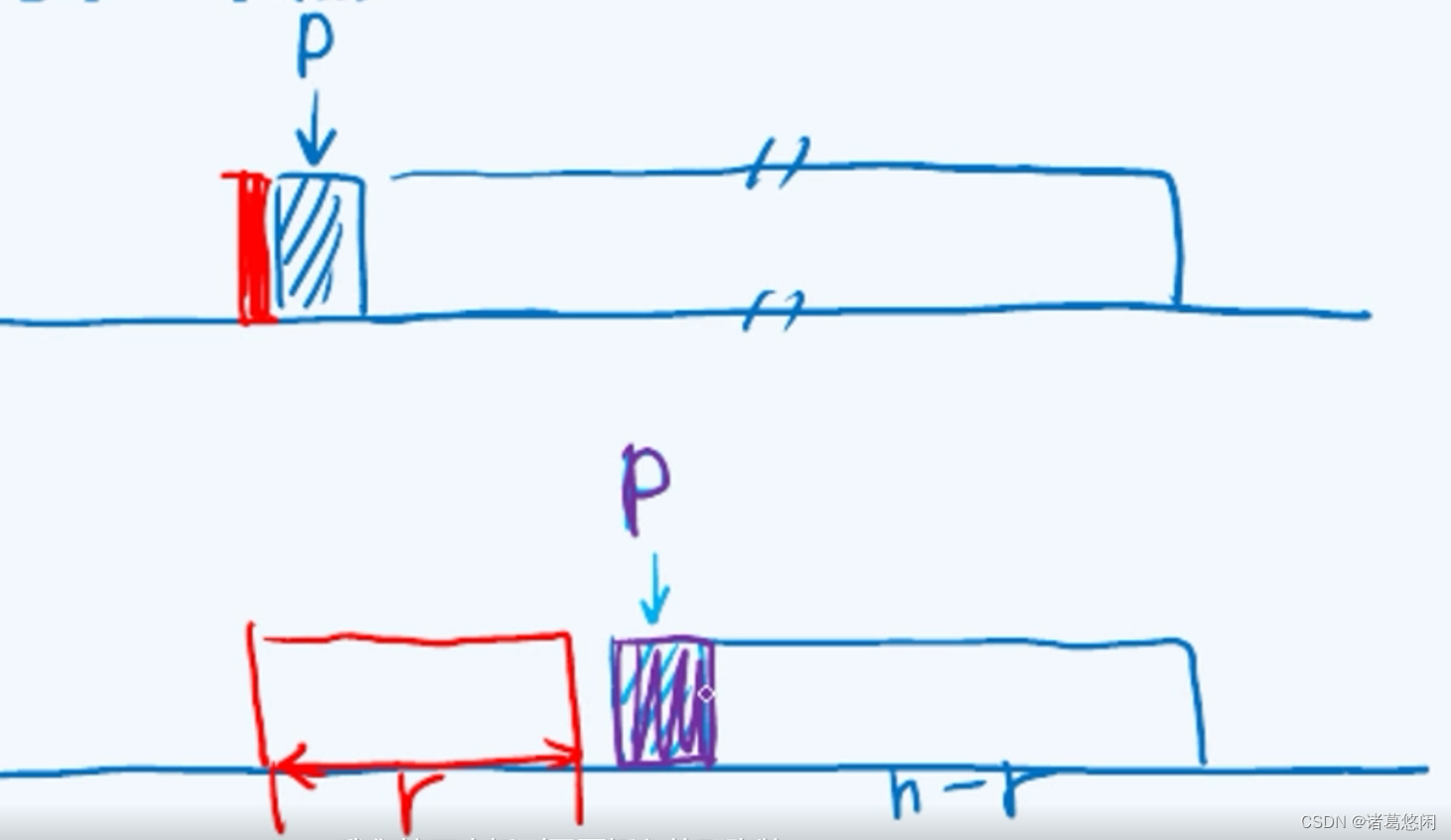
插入操作和删除操作均只需O(1)时间。查找操作search()所需时间可在O(1)至O(n)之间浮动。

当输入序列已经有序时，该算法中的每次search()操作均仅需O(1)时间，总体运行时间为O(n)。但反过来，若输出序列完全逆序，则各次search()操作所需时间将线性递增，累计共需O($n^2$)时间。在等概率条件下，平均仍需要O($n^2$)时间，换而言之，最好情况发生概率极低。

2.5 性能分析

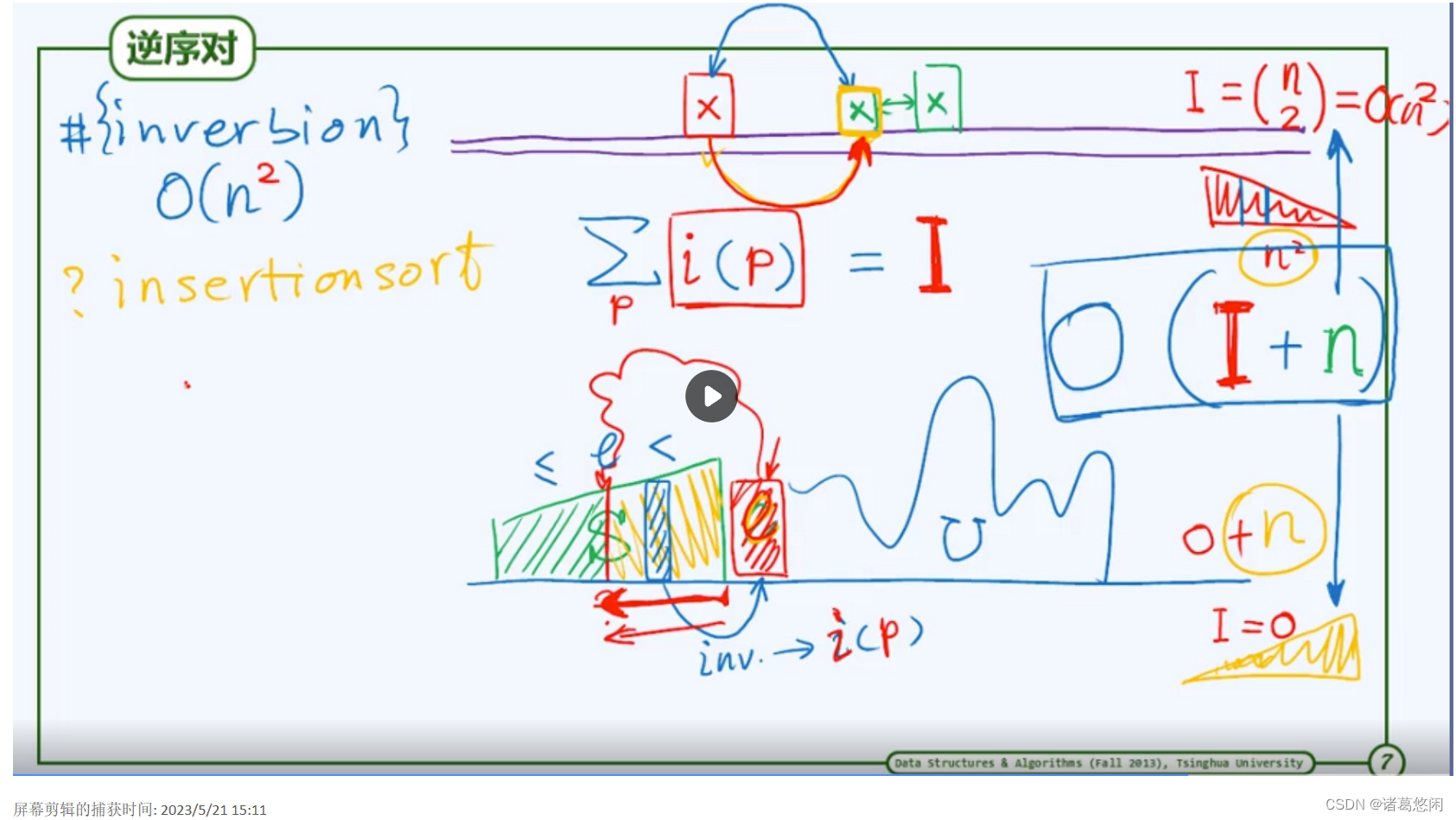
结论：
在等概率条件下，平均仍需要O($n^2$)时间。

• 假定序列中 n 个元素的数值为独立均匀地随机分布，以下结论成立：

1. 列表的插入排序算法平均需做约 $n^2/4=O(n^2)$次元素比较操作；
2. 向量的插入排序算法平均需做约 $n^2/4=O(n^2)$次元素移动操作；
3. 序列的插入排序算法过程中平均有 expected-O(logn)个元素无需移动。

3. 归并排序

3.1 二路归并算法

3.1.1 二路归并算法原理

有序列表的二路归算法同二路归并的向量排序算法，见 向量05——排序器 。能够达到与有序向量二路归并同样高的效率。

3.1.2 二路归并算法实现

算法思想：List::merge()可以将另一有序列表L中起始于节点q、长度为m的子列表，与当前有序列表中起始于节点p、长度为n的子列表做二路归并。

template <typename T> //有序列表的归并：当前列表中自p起的n个元素，与列表L中自q起的m个元素归并
ListNodePosi<T> List<T>::merge( ListNodePosi<T> p, Rank n,List<T>& L, ListNodePosi<T> q, Rank m ) {
   ListNodePosi<T> pp = p->pred; //归并之后p可能不再指向首节点，故需先记忆，以便在返回前更新
   while ( ( 0 < m ) && ( q != p ) ) //q尚未出界（或在mergeSort()中，p亦尚未出界）之前
      if ( ( 0 < n ) && ( p->data <= q->data ) ) //若p尚未出界且v(p) <= v(q)，则
         { p = p->succ; n--; } //p直接后移，即完成归入
      else //否则，将q转移至p之前，以完成归入
         { insert( L.remove( ( q = q->succ )->pred ), p ); m--; }
   return pp->succ; //更新的首节点
}

3.1.3 归并时间

        ~~~~~~~        merge()的时间成本主要消耗于其中的迭代，当且仅当后一子列表中所有节点均处理完毕时，迭代才会终止。因此，在最好情况下，共需迭代m次；而在最坏情况下，则需迭代n次。
        ~~~~~~~        总体而言，共需O(n + m)时间，线性正比于两个子列表的长度之和。

3.2 分治策略

3.2.1 实现

template <typename T> //列表的归并排序算法：对起始于位置p的n个元素排序
void List<T>::mergeSort( ListNodePosi<T>& p, Rank n ) { // valid(p) && Rank(p) + n <= size
   if ( n < 2 ) return; //若待排序范围已足够小，则直接返回；否则...
   Rank m = n >> 1; //以中点为界
   ListNodePosi<T> q = p; for ( Rank i = 0; i < m; i++ ) q = q->succ; //找到后子列表起点
   mergeSort( p, m ); mergeSort( q, n - m ); //前、后子列表各分别排序
   p = merge( p, m, *this, q, n - m ); //归并
} //注意：排序后，p依然指向归并后区间的（新）起点

3.2.2 排序时间

在子序列的划分阶段，向量与列表归并排序算法之间存在细微但本质的区别。前者支持循秩访问的方式，故可在O(1)时间内确定切分中点；后者仅支持循位置访问的方式，故不得不为此花费O(n)时间。幸好在有序子序列的合并阶段二者均需O(n)时间，故二者的渐进时间复杂度依然相等O(nlogn)。

尽管二路归并算法并未对子列表的长度做出任何限制，但这里出于整体效率的考虑，在划分子列表时宁可花费O(n)时间使得二者尽可能接近于等长。反之，若为省略这部分时间而不保证划分的均衡性，则反而可能导致整体效率的下降。

结论：
若为节省每次子列表的划分时间，而直接令 m = min(c, n/2)，其中 c 为较小的常数（比如 5），则总体复杂度反而会上升至 O($n^2$)。

4. 总结

1. 选择排序：U[o,r) + S[r,n)。从未排序元素中挑选最大者并使之就位。时间复杂度为θ($n^2$)，移动操作远远小于起泡排序。
2. 插入排序：S[o,r) + U[r,n)。从未排序元素中挑选最大者并使之就位。输入敏感型算法，最好情况1次比较，0次交换，累计O（n）时间（发生概率低）。最坏情况第k次迭代，需O（k）次比较，1次交换，累计O($n^2$)时间。
3. 归并排序：前提是在划分子列表时宁可花费O(n)时间使得二者尽可能接近于等长，渐进复杂度为O(nlogn)。