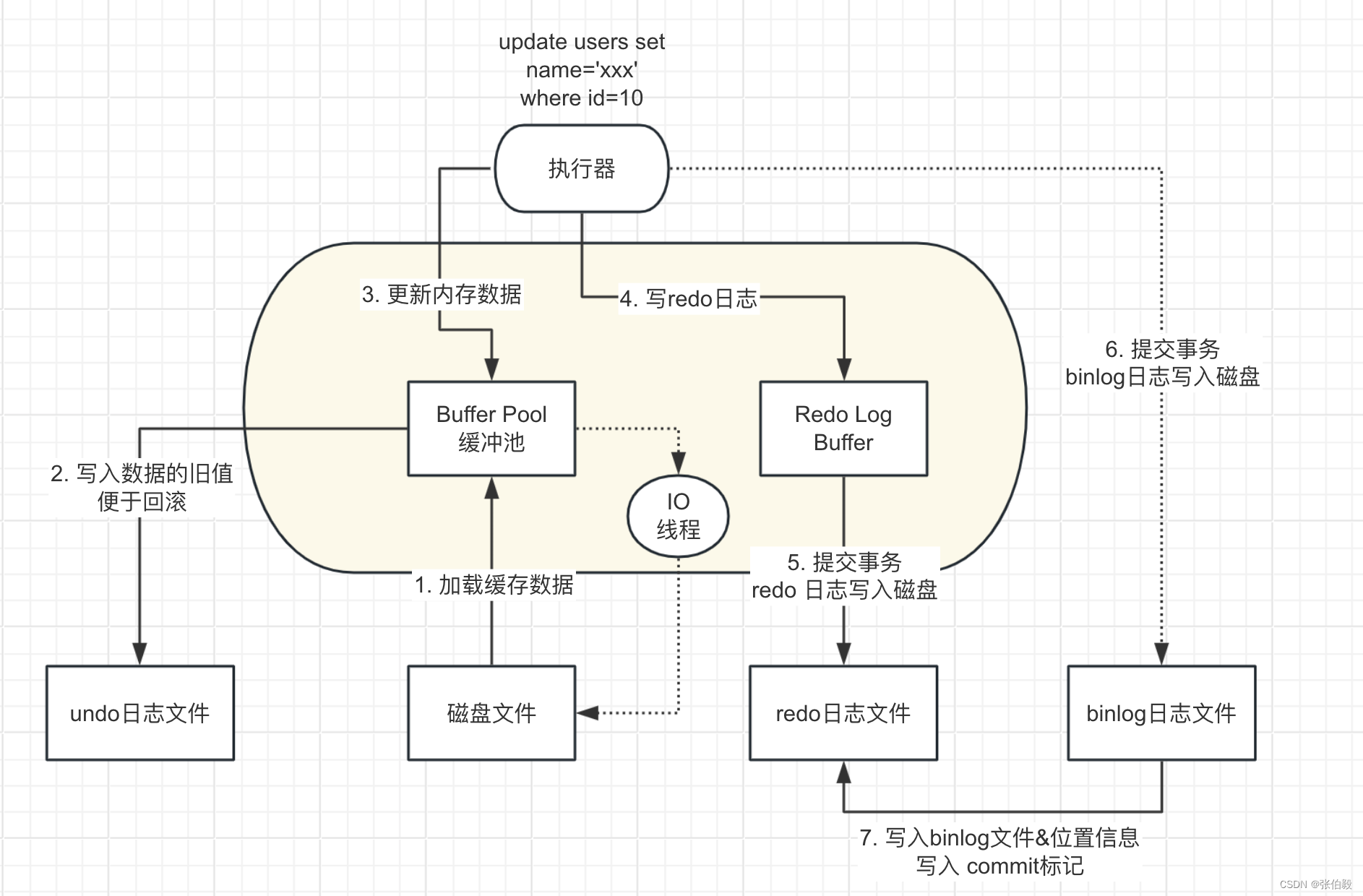
一、二叉树结尾
1、如何判断一棵树是完全二叉树。
我们可以使用层序遍历的思路,利用一个队列,去完成层序遍历,但是这里会有些许的不同,我们需要让空也进队列。如果队列里到最后只剩下空那么这棵树就是完全二叉树。具体的实现如下:
借助了,按层序走,非空节点一定是连续的。
int TreeComplete(BTNode* root)
{
assert(root);
Queue q;
QueueInit(&q);
QueuePush(&q,root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
break;
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
//判断是不是完全二叉树
//后面非空,说明非空节点不是连续的,不是完全二叉树
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front)
return false;
}
QueueDestory(&q);
return true;
}二叉树的销毁
使用后序去销毁
void TreeDestory(BTNode* root)
{
if (root == NULL)
return;
TreeDestory(root->left);
TreeDestory(root->right);
free(root);
}二、排序
1、插入排序。
把一个数据插入到有序的区间,定义一个end变量用来标识区间
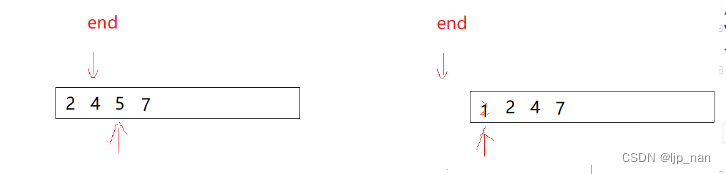
void InsertSort(int* a, int n)
{
for (int i = 1; i < n; i++)
{
//单躺排序
int temp = a[i];
int end = i - 1;
while (end >= 0)
{
if (temp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
{
//为什么要break,这里会有end为-1的位置
break;
}
}
a[end + 1] = temp;
}
}
2、希尔排序
(1)预排序--目标:数组接近有序,分组插入排序,间隔为gap分为一组,对每组数据插入排序,假设gap == 3;
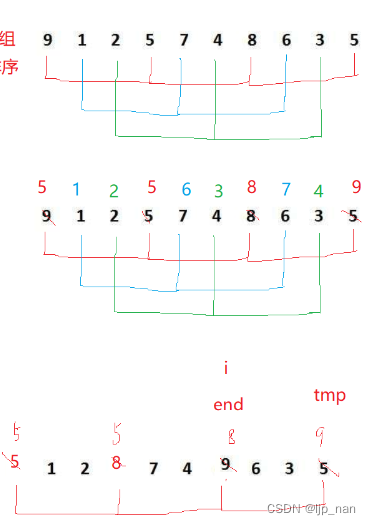
gap为3时的一趟直接插入排序
int end;
int gap = 3;
int temp = a[end+gap];
while (end >= 0)
{
if (temp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = temp;gap为3时的红色组数据的排序
void ShellSort(int* a, int n)
{
int gap = 3;
for (int i = gap; i < n; i += gap)
{
int end = i - gap;
int temp = a[end + gap];
while (end >= 0)
{
if (temp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = temp;
}
}三组都排完
void ShellSort(int* a, int n)
{
int gap = 3;
for (int j = 0; j < gap; j++)
{
for (int i = gap + j; i < n; i += gap)
{
int end = i - gap;
int temp = a[end + gap];
while (end >= 0)
{
if (temp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = temp;
}
}
}把上述代码改成i++可以减少一层循环,就变成了多组并排的方式
gap到底时多少合适呢?
gap越大,跳的越快,越不接近有序
gap越小,跳的越慢,越接近有序
gap = gap/1
gap = gap/3 + 1
//希尔排序
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 2;
for (int j = 0; j < gap; j++)
{
for (int i = gap + j; i < n; i += gap)
{
int end = i - gap;
int temp = a[end + gap];
while (end >= 0)
{
if (temp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = temp;
}
}
}
}
(2)直接插入排序
gap为1的时候为直接插入排序
gap >1的时候为预排序
时间复杂度O(n^1.3)左右的样子
3、选择排序
我们可以找到最大的交换到右边和最小的交换到左边,但是如果left == maxi,一交换mini和left的值就会把maxi里的值交换到mini上。我们需要做一个修正,maxi = mini
void Swap(int* a, int* b)
{
int temp = *a;
*a = *b;
*b = temp;
}
void SelectSort(int* a, int n)
{
//首先进行选数
int left = 0;
int right = n - 1;
while (left < right)
{
int maxi = left, mini = left;
for (int i = left; i <= right; i++)
{
if (a[i] < a[mini])
mini = i;
if (a[i] > a[maxi])
maxi = i;
}
//选数完毕交换两个数
Swap(&a[mini], &a[left]);
//进行矫正
if (left == maxi)
maxi = mini;
Swap(&a[maxi], &a[right]);
left++;
right--;
}
}选择排序最坏和最好的时间复杂度为O(n^2)
4、堆排序已经在二叉树堆已经讲过了
5、冒泡排序
void BubbleSort(int* a, int n)
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n - i; j++)
{
if(a[j] > a[j+1])
Swap(&a[j], &a[j + 1]);
}
}
}优化:
void BubbleSort(int* a, int n)
{
for (int i = 0; i < n; i++)
{
bool exchange = false;
for (int j = 0; j < n - i; j++)
{
if (a[j] > a[j + 1])
{
Swap(&a[j], &a[j + 1]);
//没有改成true证明已经有序了
exchange = true;
}
}
if (exchange == false)
break;
}
}部分有序时插入排序和冒泡排序就是有差距的。
6、快速排序
选出一个关键值key,把它放到正确的位置(最终排好序要在的位置)单趟排序
左边放比key小的,右边放比key大的
HOARE版本
左边做key,右边先走(相遇后,相遇位置正好是小的),右边找比key小的。左边找比key大的,然后交换

快排是一个递归的思想,分成左右区间,然后再排
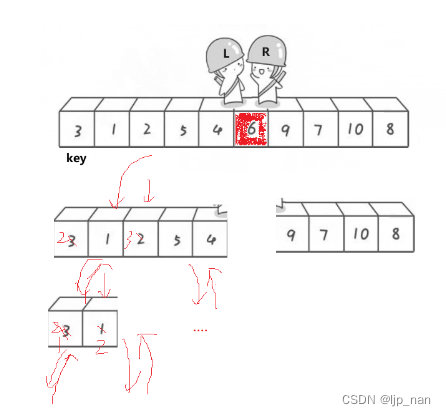
begin = 0 keyi = end
end = 1 keyi + 1 = 2 end = 1 左大于等于右不存在这个区间 (递归的出口)
void QuickSort(int* a, int left,int right)
{
if (left >= right)
{
return;
}
int keyi = left;
int begin = left, end = right;
while (left < right)
{
//相等的话没有必要交换
//不加前面的条件会越界访问
//一定先让右先走
//右边找小
while (left < right && a[right] >= a[keyi])
right--;
//左边找大
while(left < right && a[left] <= a[keyi])
left++;
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
keyi = left;
//[begin,keyi-1][keyi][keyi+1,end]
QuickSort(a,begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}时间复杂度O(NlogN)

上面有一个错误应该是n-2^i+1
最坏的情况是逆序和顺序的时候。它的时间复杂度就已经变到了O(N^2),可能会栈溢出。
优化
我们可以随机选key也可以使用三数取中法选key
int GetMidNumi(int* a, int left, int right)
{
int midi = (right + left) / 2;
if (a[left] < a[midi])
{
if (a[midi] < a[right])
{
return midi;
}
else if (a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
else //a[left] > a[midi]
{
if (a[midi] > a[right])
{
return midi;
}
else if (a[left] < a[right])
{
return left;
}
else
{
return right;
}
}
}
void QuickSort(int* a, int left,int right)
{
if (left >= right)
{
return;
}
/*int randi = left + (rand() % (right - left));
Swap(&a[left], &a[randi]);*/
//三数取中找到下标
//int keyi = left;
int midi = GetMidNumi(a, left, right);
Swap(&a[left], &a[midi]);
int keyi = left;
int begin = left, end = right;
while (left < right)
{
//相等的话没有必要交换
//不加前面的条件会越界访问
//一定先让右先走
//右边找小
while (left < right && a[right] >= a[keyi])
right--;
//左边找大
while(left < right && a[left] <= a[keyi])
left++;
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
keyi = left;
//[begin,keyi-1][keyi][keyi+1,end]
QuickSort(a,begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}那么为什么相遇的位置一定比key小
左边做key,右边先走,保证相遇位置比key要小
1、R找小,L找大没有找到,L遇到R或者就是key的位置
2、R找小找不到,R直接跟L相遇,要么就是一个比key小的位置,或者直接到keyi
类似的道理右边做key左边先走也是这样的。相遇的位置比key要大
挖坑法
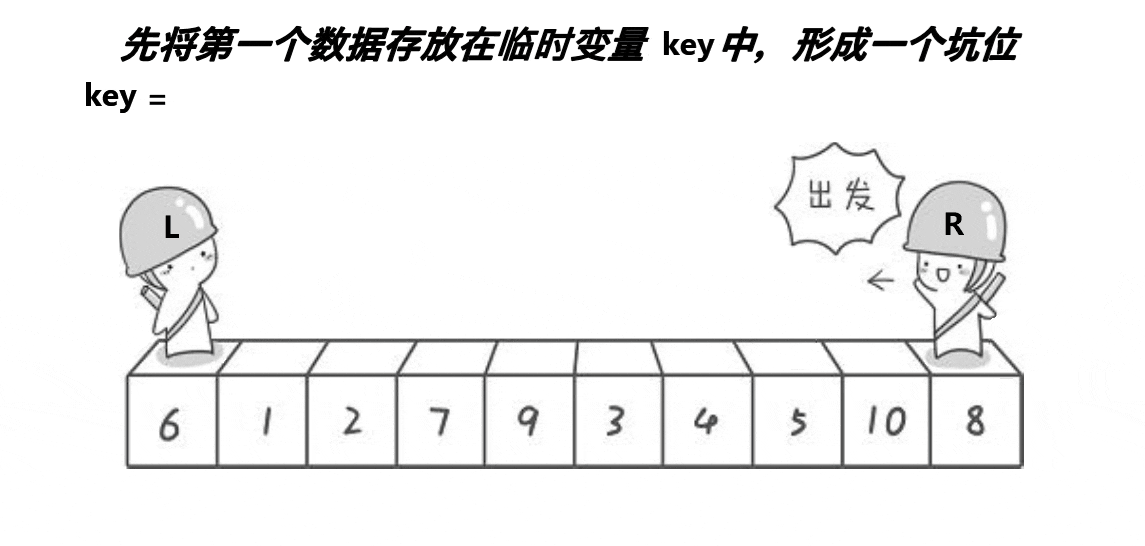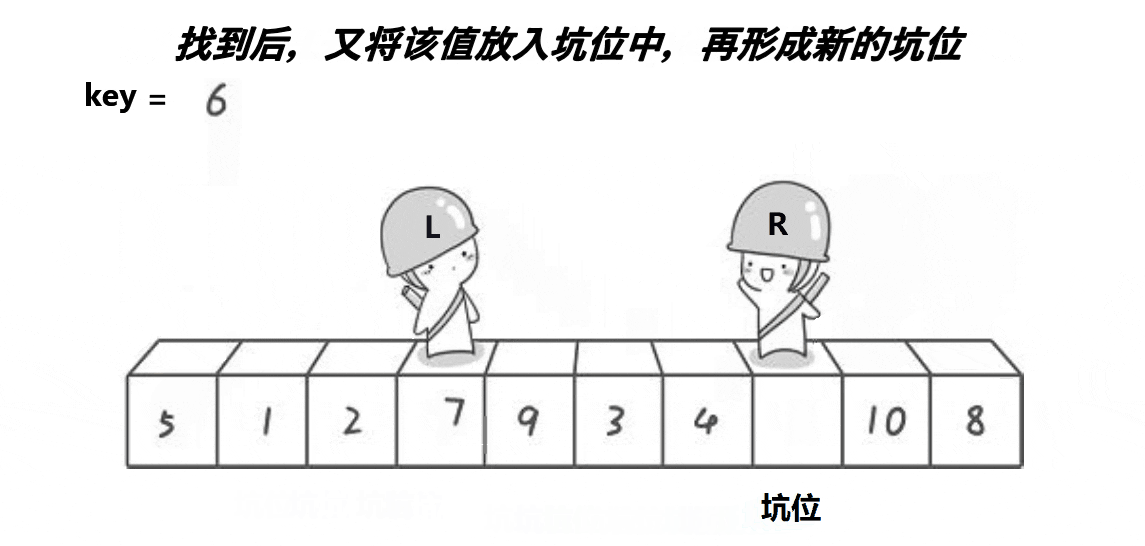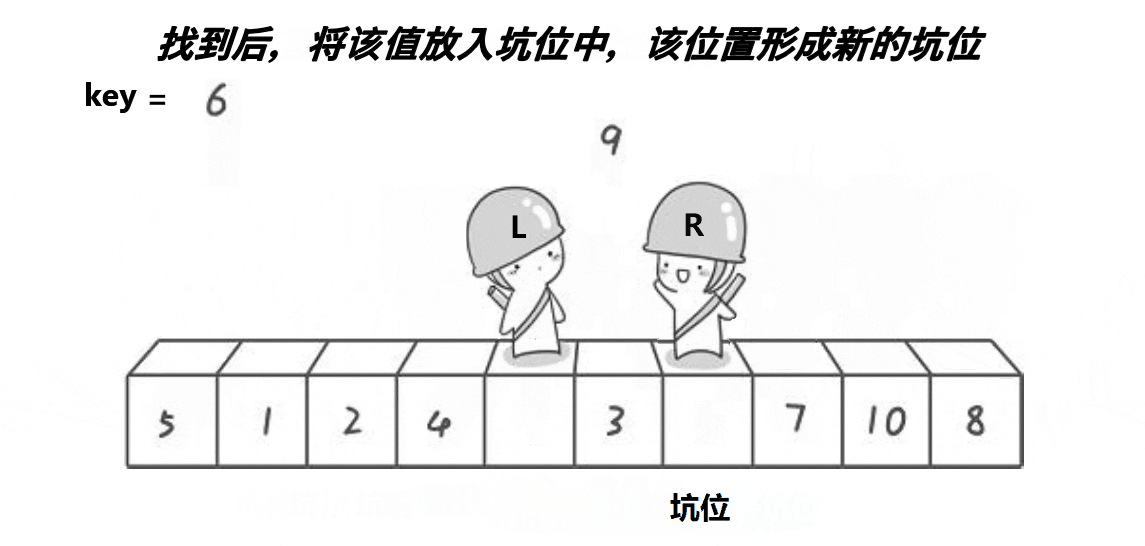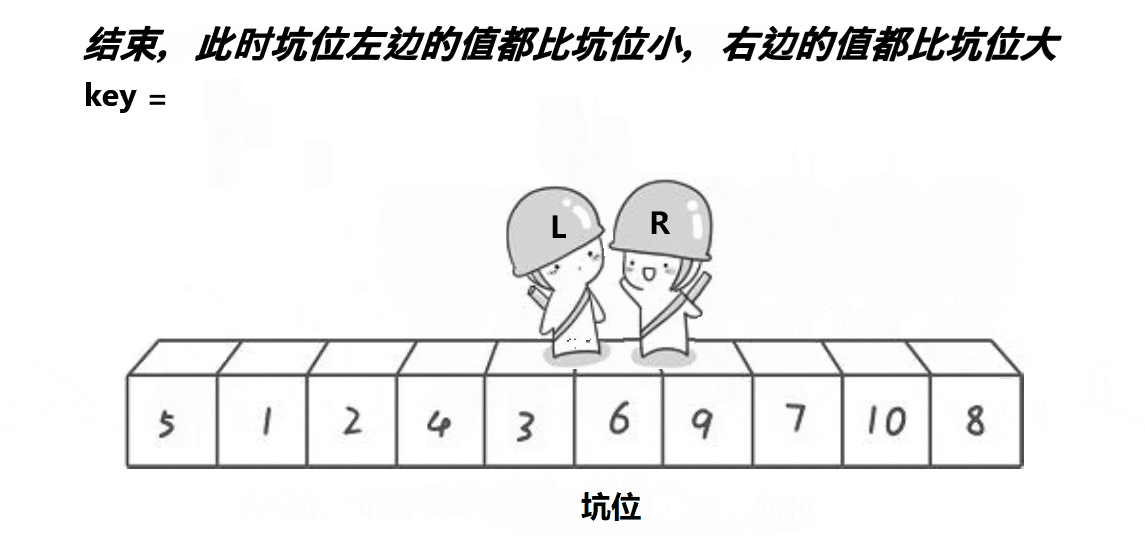
void QuickSort2(int* a, int left, int right)
{
if (left >= right)
{
return;
}
/*int randi = left + (rand() % (right - left));
Swap(&a[left], &a[randi]);*/
//三数取中找到下标
//int keyi = left;
int midi = GetMidNumi(a, left, right);
Swap(&a[left], &a[midi]);
int begin = left, end = right;
int key = a[left];
int hole = left;
while (left < right)
{
//相等的话没有必要交换
//不加前面的条件会越界访问
//一定先让右先走
//右边找小
while (left < right && a[right] >= key)
right--;
//找到以后把值放到left上面
a[hole] = a[right]; //形成新的坑位
hole = right;
//左边找大
while (left < right && a[left] <= key)
left++;
//找到后把值放到right上面
a[hole] = a[left]; //形成新的坑位
hole = left;
}
a[hole] = key;
//[begin,keyi-1][keyi][keyi+1,end]
QuickSort(a, begin, hole - 1);
QuickSort(a, hole + 1, end);
}双指针法
1、cur找到比key小的值++prev,cur和prev位置的值交换,++cur
2、cur找到比key大的值,++cur
说明:prev要么紧跟着cur(prev下一个就是cur)
prev跟cur中间间隔着比key大的一段值的区间。
把比key大的值往右翻,比key小的值,翻到左边。
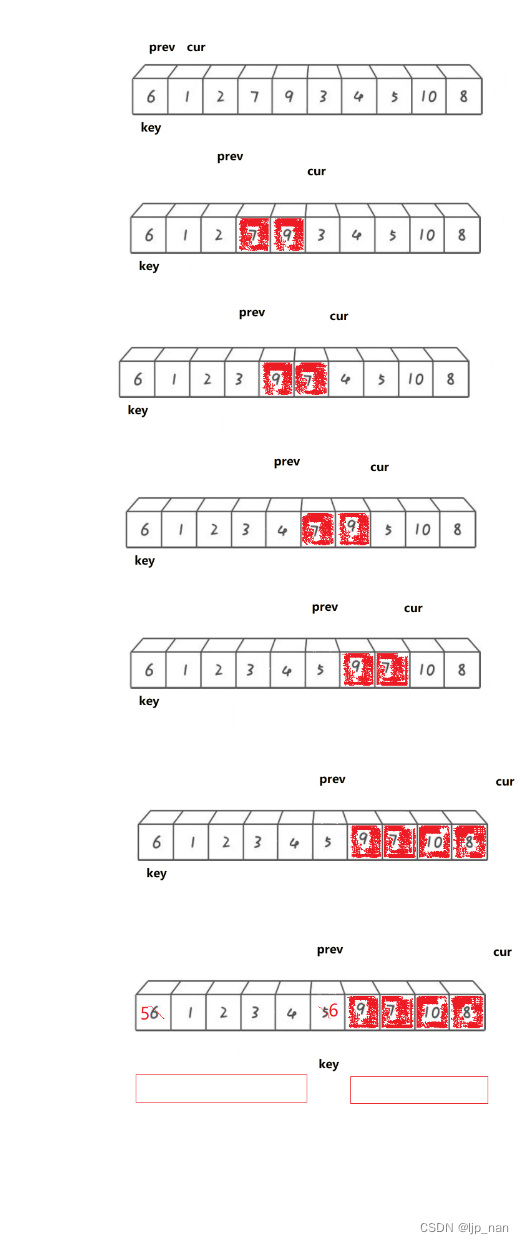
void QuickSort3(int* a, int left, int right)
{
if (left >= right)
return;
int midi = GetMidNumi(a, left, right);
Swap(&a[left], &a[midi]);
int keyi = left;
int cur = left + 1;
int prev = left;
while (cur <= right)
{
//cur找到比key小的值,++prev,然后交交换两个位置的值,cur++
//cur找到比key大的值,++cur
if (a[keyi] > a[cur]&&++prev != cur)
Swap(&a[prev], &a[cur]);
cur++;
}
Swap(&a[prev], &a[keyi]);
keyi = prev;
QuickSort3(a, left, keyi-1);
QuickSort3(a, keyi + 1, right);
}
小区间优化
到了递归的最后三层的时候,我们可以使用直接插入排序来排序,这样我们会减少百分之87.5的递归。这样的优化为小区间优化。小区间直接插入排序
void QuickSort3(int* a, int left, int right)
{
if (left >= right)
return;
//加上小区间优化
if ((right - left + 1) > 10)
{
int keyi = PartSort3(a, left, right);
QuickSort3(a, left, keyi - 1);
QuickSort3(a, keyi + 1, right);
}
else
{
InsertSort(a + left, right - left + 1);
}
}
快排的非递归
递归的问题
效率,深度太深,会栈溢出。
递归改非递归
直接改成循环
使用栈辅助改循环
如何改非递归,递归栈帧里面放的是区间。区间在变化,所以我们可以在栈里面存区间。最开始存0 - 9,进行单趟排,左区间是0 4,有区间是[ 6 ,9] 可以把这两个区间入栈,每次入栈如此反复。先入右区间,再入左区间。
1、栈里面取一段区间,单趟排序
2、单趟分割子区间入栈
3、子区间只有一个值或者不存在就不入栈
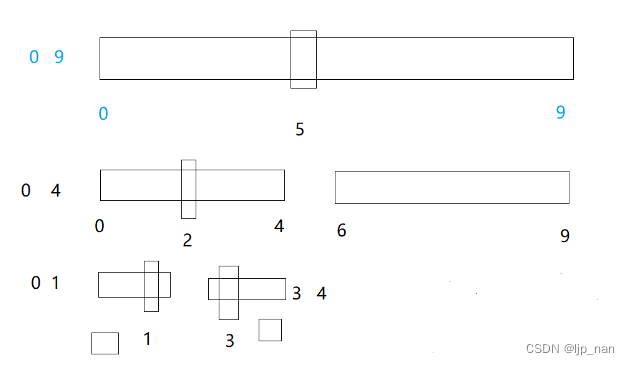
//实质就是利用自己实现的栈,来模拟编译器中的栈帧
void QuickSortNonR(int* a, int left, int right)
{
ST st;
STInit(&st);
//先让0-9区间入栈
STPush(&st, right);
STPush(&st, left);
while (!STEmpty(&st))
{
//第二步,出栈,得到区间
int begin = STTop(&st);
STPop(&st);
int end = STTop(&st);
STPop(&st);
//取出区间后进行一趟排序
int keyi = PartSort3(a, begin, end);
//然后划分出区间
//[begin,keyi-1][keyi][keyi+1,end]
if (keyi + 1 < end)
{
STPush(&st, end);
STPush(&st, keyi + 1);
}
if (begin < keyi - 1)
{
STPush(&st, keyi - 1);
STPush(&st, begin);
}
}
STDestory(&st);
}7、归并排序
两个有序区间归并:依次比较,小的尾插到新空间。
但是不满足有序区间呢。我们可以使用分治的思想,使左右区间有序。相当于二叉树的后续遍历,先分区间,再归并。时间复杂度为O(NlogN)。
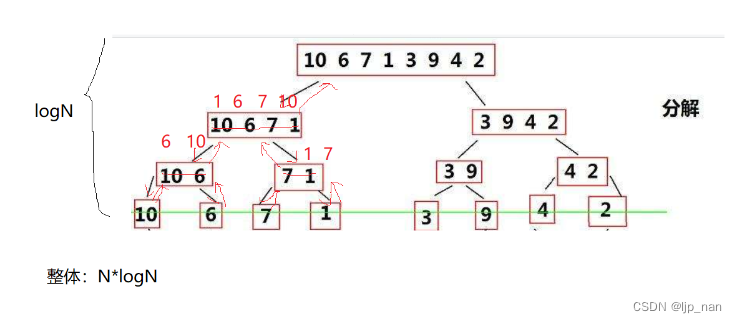
开一个临时数组,归并到临时数组,完了以后再拷贝回去。递归左区间再递归右区间
左右有序,再归并
void _MergeSort(int* a, int left, int right, int* temp)
{
//递归返回条件
if (left >= right)
{
return;
}
//首先划分区间
int mid = (right + left) / 2;
//然后使左右区间有序,采用分治的思想
//[left,mid][mid + 1,right]
_MergeSort(a, left, mid, temp);
_MergeSort(a, mid + 1, right, temp);
//接下来进行归并
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
//谁小就尾插进去
int i = left;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
temp[i++] = a[begin1++];
}
else
{
temp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
temp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
temp[i++] = a[begin2++];
}
//归并完成进行拷贝
memcpy(a + left, temp + left, sizeof(int) * (right - left + 1));
}
void MergeSort(int* a, int n)
{
int* temp = (int*)malloc(sizeof(int) * n);
if (temp == NULL)
{
perror("malloc");
return;
}
_MergeSort(a, 0, n - 1, temp);
free(temp);
}归并排序的非递归可以使用循环来实现,思路是

但是这个方法的边界处理有点麻烦
gap是归并过程中每组的个数,边界的控制
第一组:[i, i+gap-1]
第二组:[i + gap,i+2*gap-1]
那么如果遇到是奇数个可能会导致越界访问。
1、end1越界了怎么办? 不归并了

2、end1没有越界 begin2越界了,跟1一样处理
3、end2越界了,前面的都没有越界,修正end2到n-1
void MergeSortNonR(int* a, int n)
{
int* temp = (int*)malloc(sizeof(int) * n);
if (temp == NULL)
{
perror("malloc");
return;
}
int gap = 1;
//接下来进行归并
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//谁小就尾插进去
//如果是奇数个怎么办,我们可以分类讨论进行修正
if (end1 >= n || begin2 >= n)
{
break;
}
else if (end2 >= n)
{
end2 = n - 1;
}
int j = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
temp[j++] = a[begin1++];
}
else
{
temp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
temp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
temp[j++] = a[begin2++];
}
//归并完成进行拷贝
memcpy(a + i, temp + i, sizeof(int) * (end2 - i + 1));
}
gap *= 2;
}
free(temp);
}上面的排序除了归并排序外,都是内排序,也就是在内存中排序。归并排序内外都可以。
非比较排序:
1、计数排序
统计每个数据出现的个数
进行排序

总结:

void CountSort(int* a,int n)
{
//先求出范围
int max = a[0], min = a[0];
for (int i = 0; i < n; i++)
{
if (a[i] > max)
max = a[i];
if (a[i] < min)
min = a[i];
}
int range = max - min + 1;
//求出每个数出现的次数
int* countA = (int*)malloc(sizeof(int) * range);
memset(countA, 0, sizeof(int) * range);
for (int i = 0; i < n; i++)
{
countA[a[i] - min]++;
}
//进行排序
int j = 0;
for (int i = 0; i < range; i++)
{
while (countA[i]--)
{
a[j++] = i + min;
}
}
free(countA);
}2、基数排序
3、桶排序
上面的排序基本上不会用到,这里就不在描述
时间复杂度总结
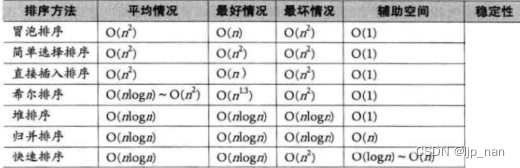
稳定性:相同数据的相对顺序是否稳定,注意是相等的数谈稳定性
稳定:冒泡排序,插入排序,归并排序。
不稳定:选择排序,希尔排序,堆排序,快速排序。