首先在了解堆排序之前我们先来回顾一下什么叫做堆吧!
基本概念
-
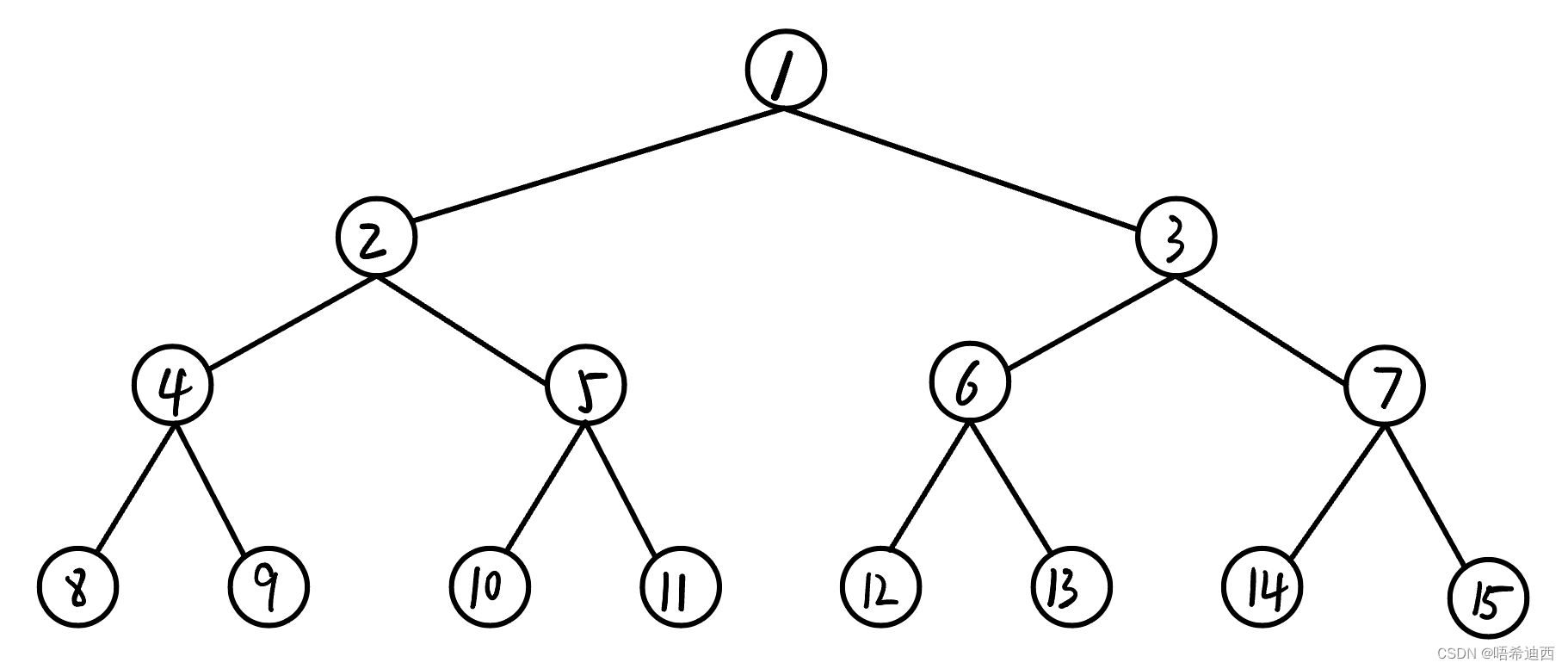
堆(Heap):是一种特殊的完全二叉树,其中每个节点的值都大于或等于(大顶堆)或小于或等于(小顶堆)其子节点的值。堆常通过数组来表示,方便快速访问和调整结构。
-
大顶堆:堆顶元素(树的根节点)是最大值,适合做降序排序的基础。
-
小顶堆:堆顶元素是最小值,适合做升序排序的基础。
让我们简单的来回顾一下大根堆是如何创建的吧!
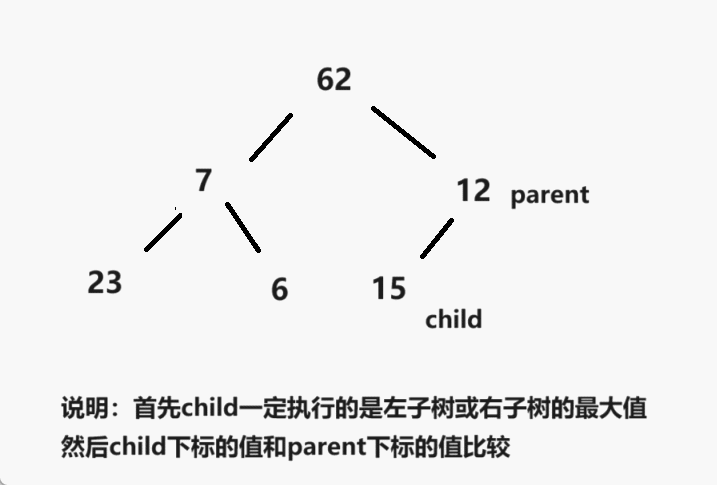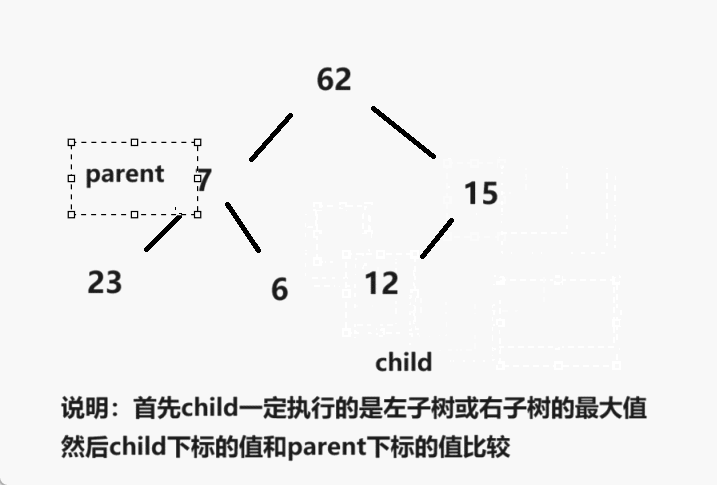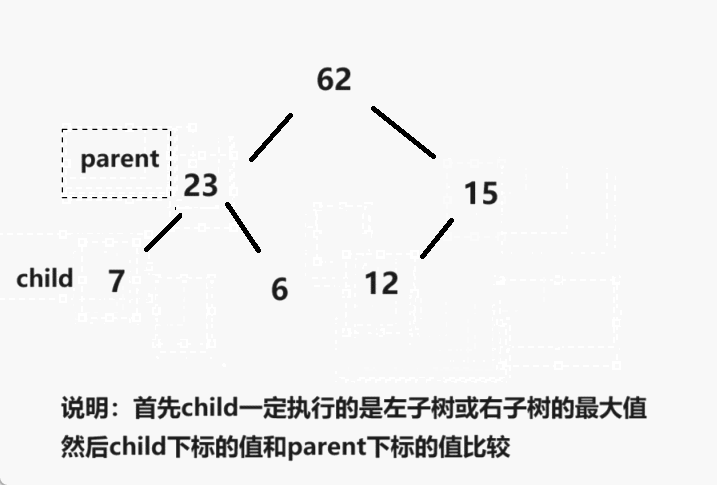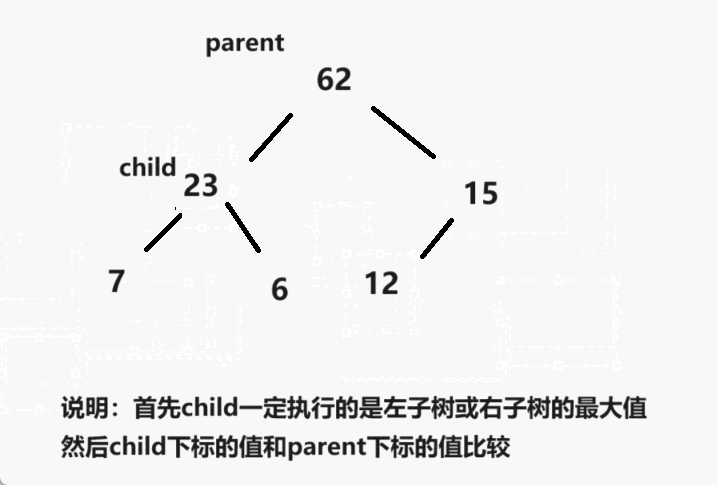
这里让我再来为大家解释一下:首先parent指向的是最后一个父亲节点的位置,然后child默认是左孩子树,但是在比较的过程中child会指向左孩子树或者是右孩子树的最大值,然后再与parent下标的值进行比较,这里因为创建的是大根堆,所以,child下标的位置比parent下标的位置大的话那么就需要交换。
那么创建大根堆的代码我就放在下面了
public static int[] createBigHeap(int[] array){
for (int parent = (array.length-1-1)/2; parent>0; parent--) {
shifDown(array,parent,array.length);
}
return array;
}
private static void shifDown(int[] array,int parent,int end){
int child = parent*2+1;
while(child<end){
if(child+1<end && array[child]<array[child+1]){
child++;
}
if(array[child] > array[parent]){
swap(array,parent,child);
parent = child;
child = parent*2+1;
} else {
break;
}
}
}通过上面我们已经了解了什么是堆,那么如何进行堆排序呢?
首先堆排序是一种高效的排序算法,它利用了一种叫做“堆”的特殊数据结构来实现。堆是一个近似完全二叉树,其中每个父节点的值都大于或等于其子节点的值(在大顶堆中)或者小于或等于其子节点的值(在小顶堆中)。
排序阶段包括以下重复步骤,直到整个序列变为有序:
- 将堆顶元素(即当前最大或最小值)与序列的最后一个元素交换位置。这样,最大值(或最小值)就被放置在了正确的位置(序列的末尾)。
- 将剩下的元素重新调整为堆,确保去掉一个元素后仍然满足堆的性质。这不包括刚刚被交换到末尾的元素。
- 重复上述交换和调整堆的过程,每次都将下一个最大(或最小)元素移到已排序部分的末尾。
代码实现:
public static int[] heapsort(int[] array){
createBigHeap(array);
int end = array.length-1;
while(end>=0){
swap(array,0,end);
shifDown(array,0,end);
end--;
}
return array;
}
时间复杂度:堆排序的平均和最坏情况时间复杂度都是O(n log n),其中n是数组长度。这是因为构建堆的时间复杂度为O(n),而每次调整堆的时间复杂度为O(log n),总共需要调整n-1次。
空间复杂度:堆排序是原地排序算法,除了排序过程中的一些临时变量外,不需要额外的存储空间,因此其空间复杂度为O(1)。
稳定性:堆排序是一种不稳定的排序算法,因为在调整堆的过程中相等的元素可能会改变它们的原始相对位置。