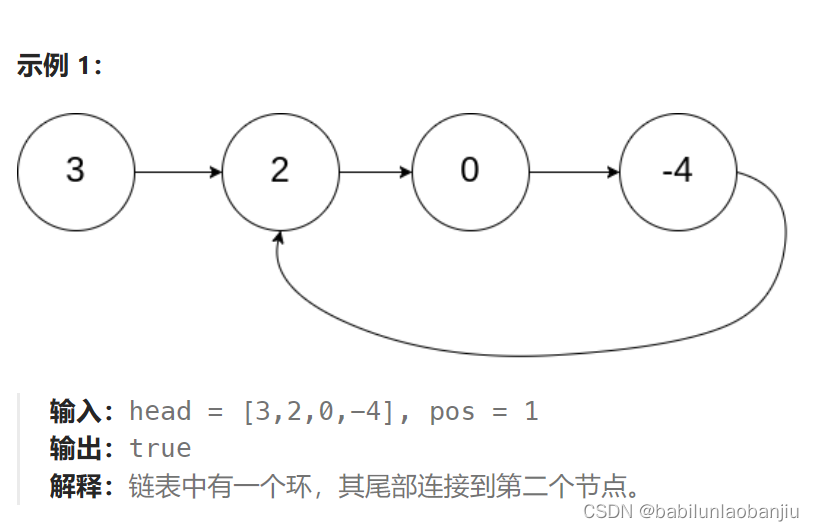
二、思路

1.使用快慢指针，快指针一次走两步，慢指针一次走一步，二者相对速度为1

2.当慢指针刚好进入环时，设二者的相对距离为N

3.如果链表中存在环，快指针就会追上慢指针。快慢指针就会相遇。

4.设环的结点数量为C

三、代码

bool hasCycle(struct ListNode *head) {
    struct ListNode*fast=head;
    struct ListNode*slow=head;
    while(fast&&fast->next)
    {
        fast=fast->next->next;
        slow=slow->next;
        if(fast==slow)
        return true;
    }
    return false;

}

因为快指针一次性走两步，所以要对fast  和   fast->next  进行判断是否为NULL。

fast  指针 一次走两步，slow  一次性走 一步，二者相对速度为1，所以，fast 一定能追上 slow。二者在有环存在的情况下，一定能相遇。

四、思考（如果fast一次性走3步能否成功）

fast  指针 一次走3步，slow  一次性走 1步，二者相对速度为2，所以，fast 一定能追上 slow。二者在有环存在的情况下，可能遇见，也可能错过。

1.二者的相对距离N为偶数时，

N%2==0，说明二者一定能遇见，说明fast一次走3步能成立。

2.二者的相对距离N为奇数时，

N%2==1，说明二者距离减到 1时，没有遇见，距离再次减2，距离为-1.  第一轮无法相遇

这时，快慢指针的距离为C-1

（1）当C为偶数时（C-1为奇数）

这时二者的相对距离C-1为奇数，（C-1）%2==1.

可以说明 ：

说明二者距离减到 1时，没有遇见，距离再次减2，距离为-1.  第一轮无法相遇

这时，快慢指针的距离为C-1，一直陷入死循环，无法成功

（2）当C为奇数时（C-1为偶数）

这时二者的相对距离C-1为偶数，（C-1）%2==0.

可以说明 ，在第二轮的时候， 二者一定能遇见，说明fast一次走3步能成立

3.逻辑总结：

当慢指针刚好进入环时，二者的相对距离为N  环的结点数量为C

1.当N为偶数时，fast一次走3步能成立

2.当N为奇数时并且C为奇数时，fast一次走3步也能成立

3.当N为奇数并且C为偶数时，fast一次走3步不能成立

4.数学方法思考

设进入环之前的路程为L

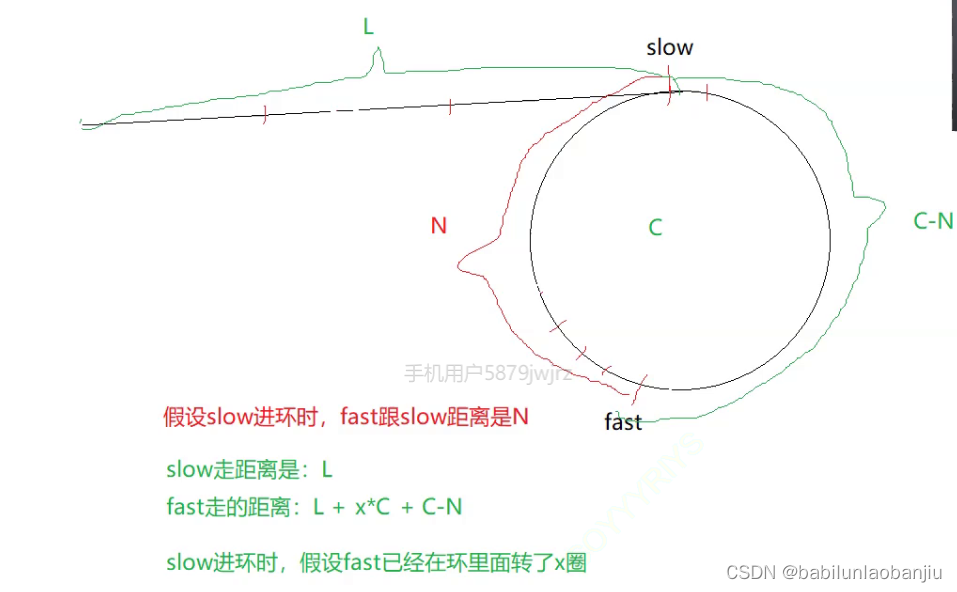
因为：fast  指针 一次走3步，slow  一次性走 1步

所以： 3*L  == L + x*C + C - N

化简得： 2*L == （X+1）*C - N

观察此式子 等号左边  2*L 一定是 偶数 ，所以等号 右边一定也是 偶数

此时，N和C可以都是 奇数，也可以都是 偶数,

当N是奇数，C是偶数 时    （X+1）*C - N是一个奇数！

说明：N不能是奇数的同时C是偶数，上述总结的  （3.当N为奇数并且C为偶数时，fast一次走3步不能成立）  这种情况不存在

综上所有的分析：fast  一次性走3 步 也可以成功！！！