先上公式：

• 递归算法的时间复杂度 = 递归次数 x 每次递归消耗的时间颗粒数
• 递归算法的空间复杂度 = 递归深度 x 每次递归消耗的内存空间大小

---

注意：

• 时间复杂度指的是在执行这一段程序的时候，所花费的全部的时间，即时间的总和
• 而空间复杂度可不是你在执行这段程序的时候，所花费的内存空间大小的总和！它指的是在执行这段程序的过程中，可以同时占据内存空间的最大空间数

---

解释：其实所有的递归法图像化以后，都可以写做N叉树的形式，下面我就以二叉树为例讲解

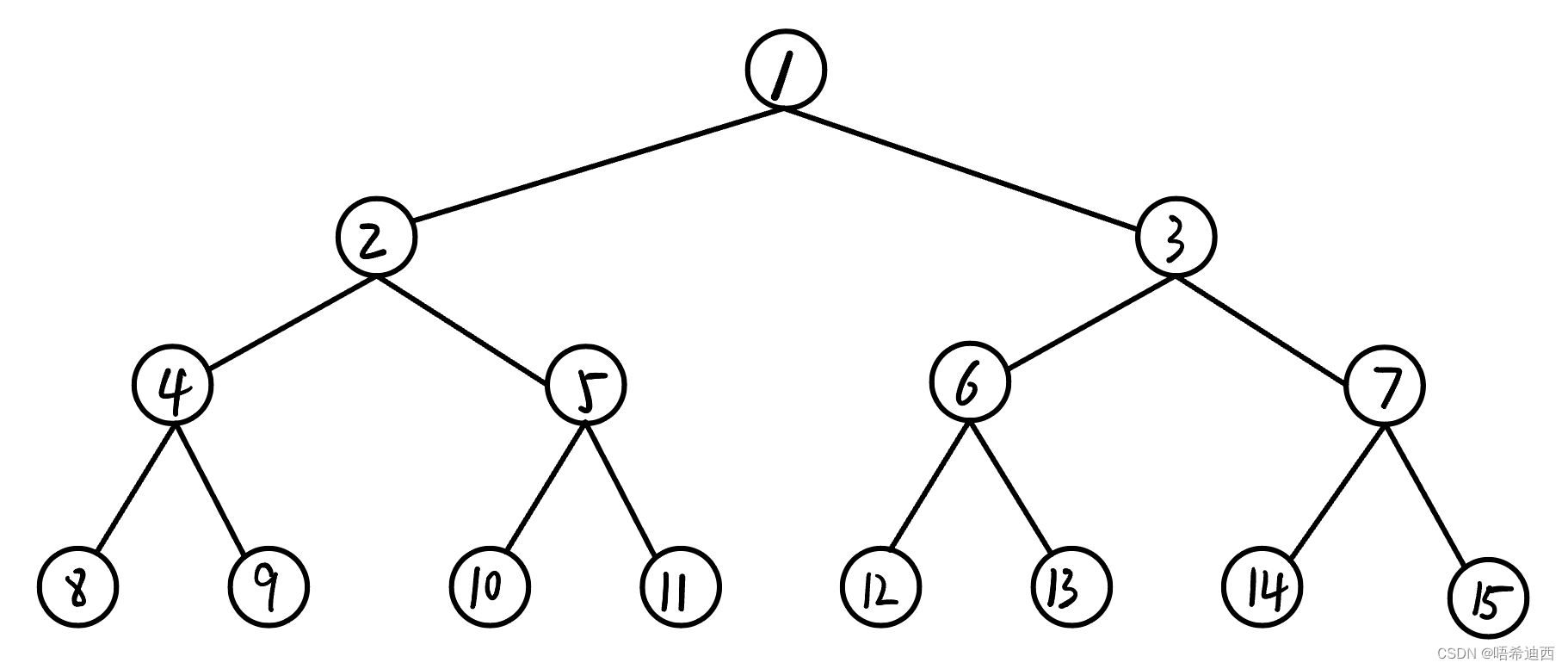
每个节点都是一个递归体，如果计算时间复杂度，那么每个节点都需要被执行，所以时间复杂度应该是15 x 每个节点所消耗的时间；

但是空间复杂度可不是15 x 每个节点所消耗的内存空间；因为在节点1处向下递归时，是将节点1中的同一个变量传递给节点2和节点3的，并没有开辟新的变量，将一个变量传递给节点2，另一个传递给节点3；

在节点4，5，6，7处的递归体中，这四个递归体并不是同一时间执行的，只有在执行完节点4的递归体后，才会执行节点5的递归体；同时这四个节点的递归函数体可是一样的，假设递归体中要向下传递的参数是a，那么在执行完节点4后，参数a就被释放掉了，然后到节点5，又创建了节点5中的参数a，执行完节点5这个参数a又被释放掉了；所以不可能说节点4，5，6，7的所有参数a同时存在，因此在二叉树的这一层中，只会存在一个参数a；

这样一来，二叉树有几个深度，就有几个同时存在的参数a；而在二叉树中同一层上，是不会同时存在参数a的；