NO.3

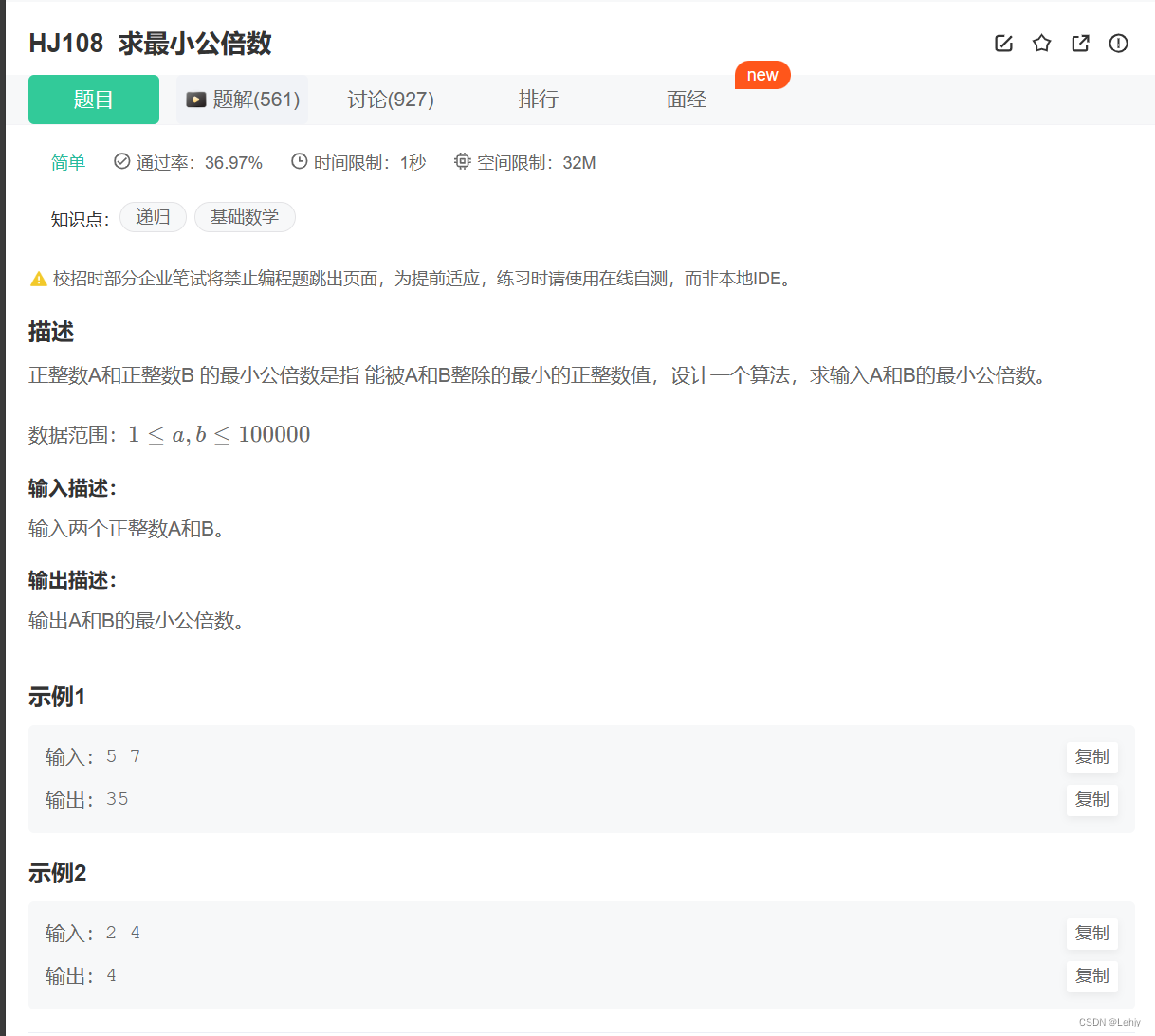
思路：相乘除以最大公约数等于最小公倍数。最小公倍数等于gcd（a，a%b）递归直到b等于0。
代码实现：

#include <iostream>
using namespace std;

int gcd(int a,int b)
{
    if(b==0) return a;
    return gcd(b,a%b);
}

int main() {
    int a,b;
    cin>>a>>b;
    cout<<(a*b/gcd(a,b))<<endl;
}

NO.2

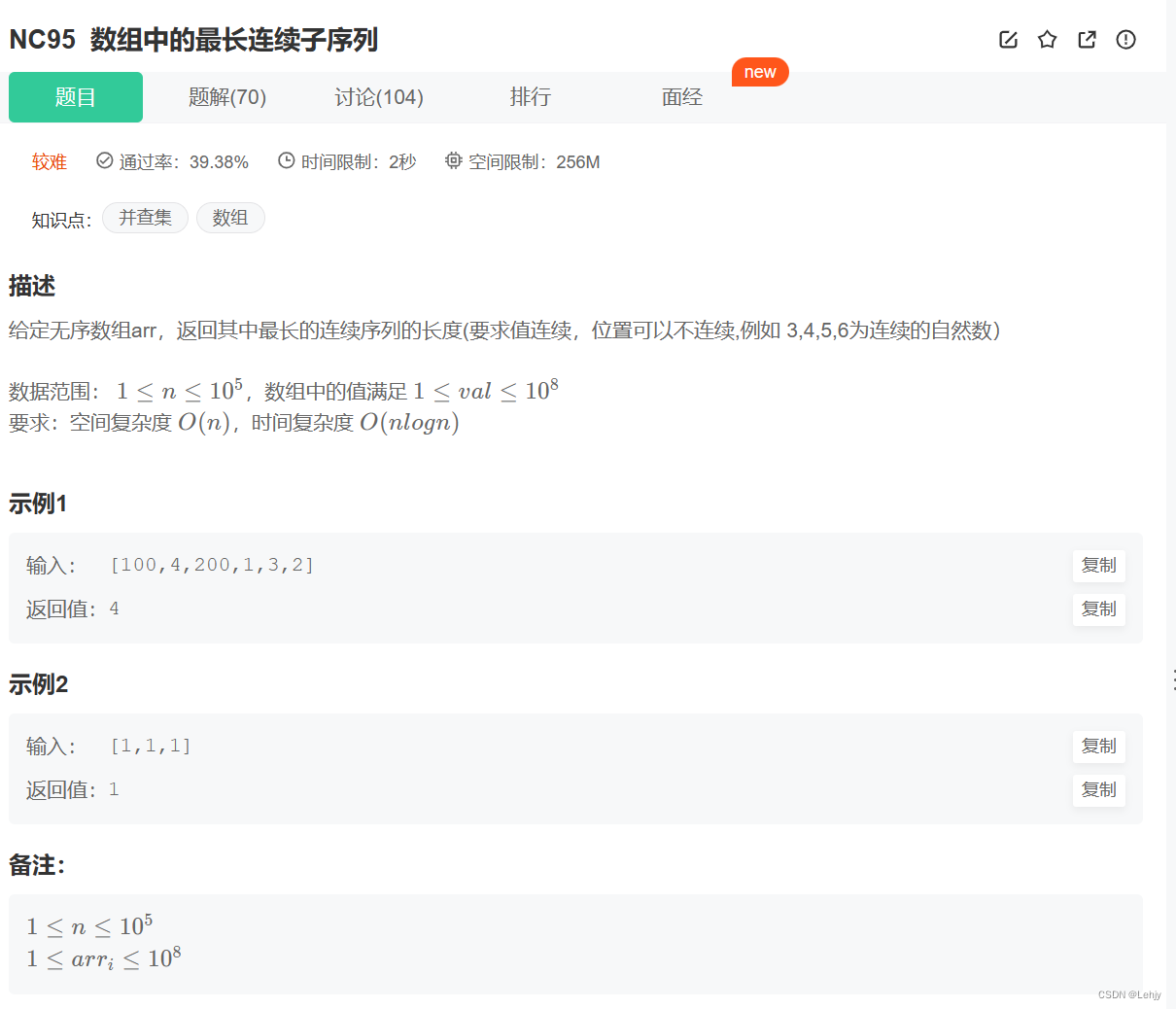
思路：排序+双指针。先排序，定义两个自变量表示下标，i进行遍历，j=i+1，如果j位置的值减去j-1位置de值为1，count++，j++，如果j位置的值减去j-1位置de值为0，j++，否则break跳出循环。最后更新长度。

代码实现：

class Solution {
public:
    
    int MLS(vector<int>& arr) {
        int ret=0,n=arr.size();
        sort(arr.begin(),arr.end());
        for(int i=0;i<n;)
        {
            int j=i+1,count=1;
            while(j<n)
            {
                if(arr[j]-arr[j-1]==1)
                {
                    count++;
                    j++;
                }
                else if(arr[j]-arr[j-1]==0)
                {
                    j++;
                }
                else
                {
                    break;
                }
            }
            ret=max(ret,count);
            i=j;
        }
        return ret;
    }
};

NO.3

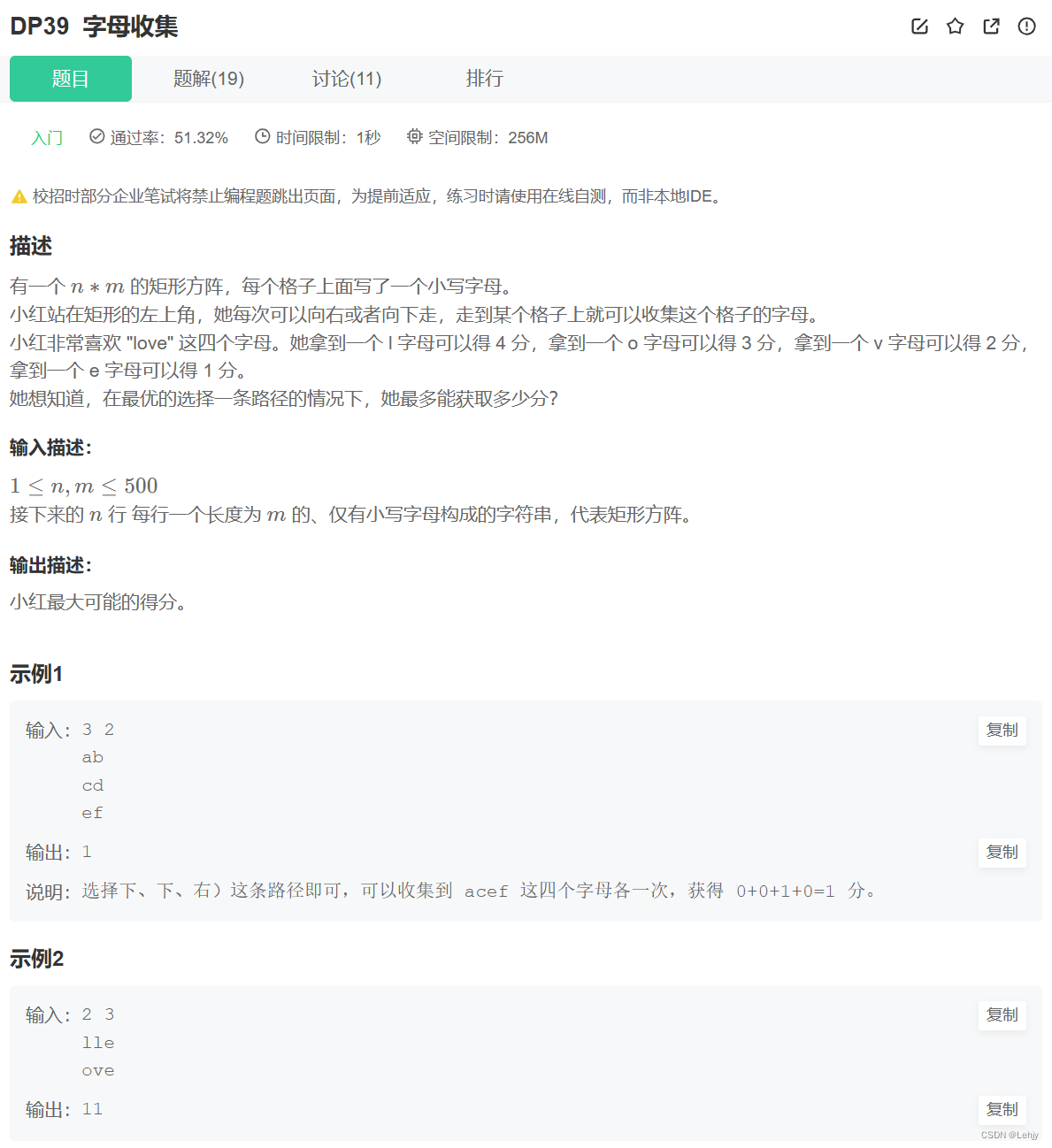
思路：dp。

代码实现：

#include <iostream>
using namespace std;

const int N=510;
char arr[N][N];
int dp[N][N];
int main() {
    int m,n;
    cin>>m>>n;
    for(int i=1;i<=m;i++)
    {
        for(int j=1;j<=n;j++)
        {
            cin>>arr[i][j];
    
        }
    }
    for(int i=1;i<=m;i++)
    {
        for(int j=1;j<=n;j++)
        {
            int t=0;
            if(arr[i][j]=='l') t=4;
            else if(arr[i][j]=='o') t=3;
            else if(arr[i][j]=='v') t=2;
            else if(arr[i][j]=='e') t=1;
            dp[i][j]=max(dp[i-1][j],dp[i][j-1])+t;
    
        }
    }

    cout<<dp[m][n]<<endl;
    return 0；
}