一、题目描述

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：

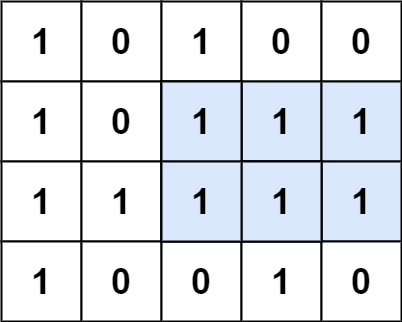
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：6
解释：最大矩形如上图所示。

示例 2：

输入：matrix = [["0"]]
输出：0

示例 3：

输入：matrix = [["1"]]
输出：1

提示：

• rows == matrix.length
• cols == matrix[0].length
• 1 <= row, cols <= 200
• matrix[i][j] 为 '0' 或 '1'

二、解题思路

1. 计算每个点的连续高度：对于矩阵中的每一行，计算从当前行向上连续的’1’的个数，将这些个数作为一个直方图的高度。
2. 使用单调栈求解最大矩形：在计算每一行的直方图高度后，使用单调栈来找出直方图中最大矩形的面积。单调栈可以用来快速找出每个柱子左右两边第一个比它矮的柱子。
3. 更新最大面积：每找到一个矩形的面积，就与当前记录的最大面积进行比较，取较大值作为新的最大面积。

三、具体代码

import java.util.Stack;

public class Solution {
    public int maximalRectangle(char[][] matrix) {
        if (matrix == null || matrix.length == 0) {
            return 0;
        }
        int maxArea = 0;
        int[] heights = new int[matrix[0].length];
        
        for (int i = 0; i < matrix.length; i++) {
            // 更新直方图的高度
            for (int j = 0; j < matrix[0].length; j++) {
                if (matrix[i][j] == '1') {
                    heights[j]++;
                } else {
                    heights[j] = 0;
                }
            }
            // 使用单调栈求解最大矩形
            maxArea = Math.max(maxArea, largestRectangleArea(heights));
        }
        
        return maxArea;
    }
    
    private int largestRectangleArea(int[] heights) {
        Stack<Integer> stack = new Stack<>();
        int maxArea = 0;
        int p = 0;
        
        while (p < heights.length) {
            if (stack.isEmpty() || heights[p] >= heights[stack.peek()]) {
                stack.push(p);
                p++;
            } else {
                int h = heights[stack.pop()];
                int w = stack.isEmpty() ? p : p - stack.peek() - 1;
                maxArea = Math.max(maxArea, h * w);
            }
        }
        
        while (!stack.isEmpty()) {
            int h = heights[stack.pop()];
            int w = stack.isEmpty() ? heights.length : heights.length - stack.peek() - 1;
            maxArea = Math.max(maxArea, h * w);
        }
        
        return maxArea;
    }
}

四、时间复杂度和空间复杂度

1. 时间复杂度

• 遍历矩阵中的每个元素需要 O(m * n) 的时间，其中 m 是矩阵的行数，n 是矩阵的列数。
• 对于每一行，使用单调栈计算最大矩形面积的时间复杂度是 O(n)，因为每个元素最多被压入和弹出栈一次。
• 因此，总的时间复杂度是 O(m * n)。

2. 空间复杂度

• 需要一个额外的数组 heights 来存储每一行的直方图高度，其大小为 O(n)。
• 单调栈 stack 的大小最大也为 O(n)，因为栈中最多存储一行的所有列索引。
• 因此，总的空间复杂度是 O(n)。

综上所述，这段代码的时间复杂度是 O(m * n)，空间复杂度是 O(n)。

五、总结知识点

1. 二维数组和字符串处理：

• 使用二维字符数组 char[][] matrix 来表示矩阵，其中每个元素是 ‘0’ 或 ‘1’。
• 使用一维整型数组 int[] heights 来存储每一行的直方图高度。

2. 栈（Stack）的使用：

• 利用 Stack<Integer> 来实现单调栈，用于快速计算最大矩形面积。
• 栈的特点是后进先出（LIFO），在处理直方图时，可以保持栈内元素的单调性（递增或递减）。

3. 单调栈算法：

• 单调栈是一种特殊的栈结构，用于解决一类特定的问题，如找到每个元素左边或右边第一个比它大或小的元素。
• 在本题中，单调栈用于找到每个直方图柱子左右两边第一个比它矮的柱子，从而计算矩形的面积。

4. 动态规划思想：

• 虽然代码中没有直接使用动态规划，但是在计算直方图高度时，实际上是在使用动态规划的思想。
• 对于每一行，直方图的高度是基于上一行的高度和当前行的字符值计算得出的。

5. 遍历和迭代：

• 使用嵌套的 for 循环来遍历矩阵的每一行和每一列。
• 在 largestRectangleArea 方法中，使用 while 循环来迭代直方图的高度数组，并使用栈来计算最大矩形面积。

6. 数学和逻辑运算：

• 在计算最大矩形面积时，使用了基本的数学运算（乘法和比较）。
• 使用条件语句（if-else）和逻辑运算符来控制程序的流程。

7. 函数和方法的定义与调用：

• 定义了 maximalRectangle 和 largestRectangleArea 两个方法，分别用于解决整个问题和解决子问题（计算直方图的最大矩形面积）。
• 在主方法中调用子方法，实现了解耦和模块化。

以上就是解决这个问题的详细步骤，希望能够为各位提供启发和帮助。