Raft算法
Raft是如何解决成员变更问题的
在日常工作中,你可能会遇到服务器故障的情况,这时你需要替换集群中的服务器。如果遇到需要改变数据副本数的情况,则需要增加或移除集群中的服务器。总的来说,在日常工作中,集群中的服务器数量是会发生变化的。也许你会问,Raft算法是共识算法,它对集群成员进行变更时(比如增加2台服务器),会不会因为集群分裂出现两个领导者呢?在我看来,的确会出现这个问题,因为Raft算法的领导者选举是建立在"大多数"的基础之上,那么当成员变更,集群成员发生变化时,就可能同时存在新旧配置的两个"大多数",出现两个领导者,从而破坏了Raft集群的领导者唯一性,影响了集群的运行。成员变更不仅是Raft算法中比较难理解也非常重要的一部分,而且是Raft算法中唯一被优化和改进的部分。比如,最初成员变更的是联合共识(Joint Consensus),但这个方法实现起来很难,后来Raft算法的作者就提出了一种改进后的方法,单节点变更(single-server change).
在分析之前,我们先介绍以下"配置"这个词。配置是成员变更中一个非常重要的概念,可以这样理解:配置用于说明集群由哪些节点组成,是集群各节点地址信息的集合。比如节点A、B、C组成的集群配置就是【A,B,C】集合。
假设有一个由节点A、B、C组成的Raft集群,现在我们需要增加数据副本数。即增加两个副本(也就是增加两台服务器),扩展为由节点A、B、C、D、E这5个节点组成的新集群,如图所示。那么在集群配置变更时,Raft算法是如何保障集群稳定运行,而不出现两个领导者呢?老话说的好,认识问题,才能解决问题。为了更好地理解单节点变更地方法,我们先来看一看成员变更时到底会出现什么样的问题
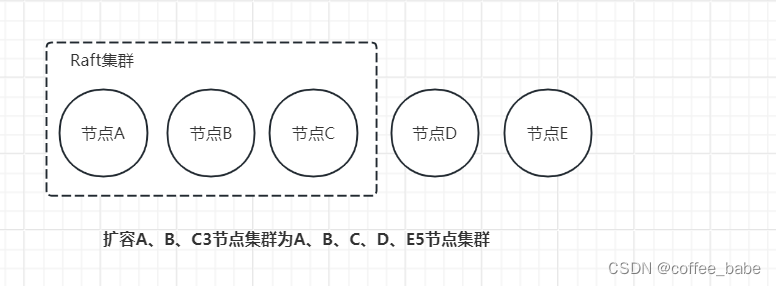
成员变更问题
在我看来,上图所示的集群中进行成员变更的最大风险是,可能会同时出现两个领导者。比如在进行成员变更时,节点A、B、C之间发生了分区错误,节点A、B组成旧配置中的"大多数",也就是变更前的3节点集群中的"大多数",那么这时的领导者(节点A)依旧是领导者。然后,节点C和新节点D、E组成了新配置的"大多数",也就是变更后的5节点集群中的"大多数",它们可能会选举出新的领导者(比如节点C)。那么这时旧出现了同时存在两个领导者的情况,如图所示
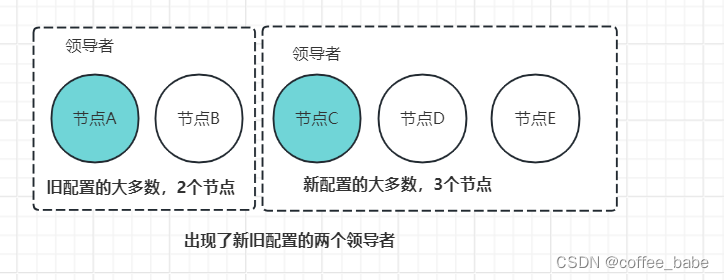
两个领导者违背了"领导者的唯一性"的原则,进而影响到集群的稳定运行。如何解决这个问题呢?也许有人想到下面这种解决办法。
集群在启动时的配置是固定的,不存在成员变更,此时,Raft算法的领导者选举能保证只有一个领导者,也就是说,这时不会出现多个领导者的问题,那么我们是否可以先将集群关闭再启动新集群,即先关闭节点A、B、C组成的集群,待成员变更后,再启动由节点A、B、C、D、E组成的新集群?
在我看来,这个方法不可行。为什么呢?因为每次变更都要重启集群,意味着在集群变更期间服务不可用,这势必会影响用户体验。想象以下,你正在玩王者荣耀,但时不时会受到系统弹出的对话框,通知你,系统升级,游戏暂停3分钟。这种体验糟糕不糟糕?既然这种办法影响用户体验,根本行不通,那应该怎样解决成员变更的问题呢?最常用的方法就是单节点变更。
注意。
成员变更的问题主要在于成员变更时,可能存在新旧配置的两个"大多数",导致集群中同时出现两个领导者,破坏了Raft算法的领导者的唯一性原则,影响了集群的稳定运行
如何通过单节点变更解决成员变更问题
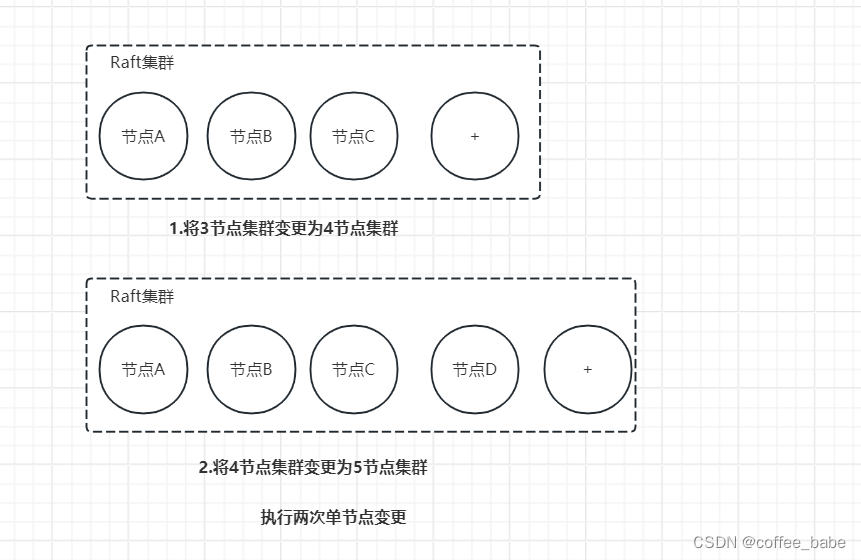
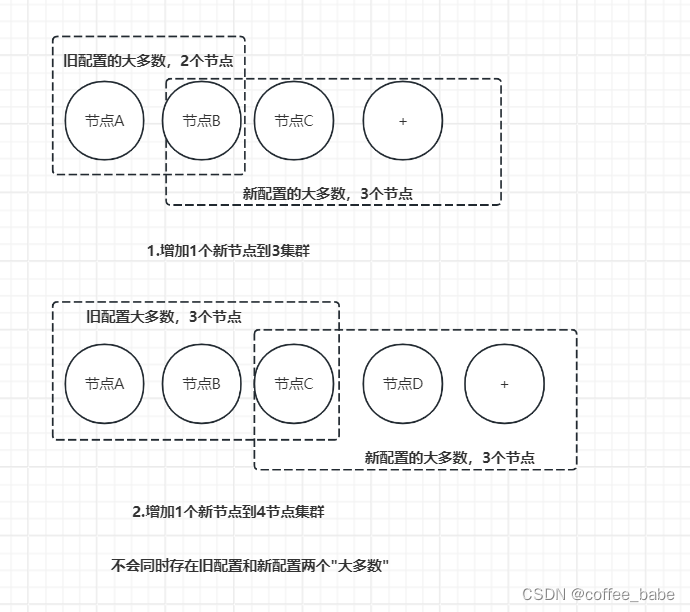
单节点变更就是通过一次变更一个节点实现成员变更。如果需要变更多个节点,则需要执行多次单节点变更。比如在将3节点集群扩容为5节点集群时,你需要执行两次单节点变更,先将3节点集群变更为4节点集群,再将4节点集群变更为5节点集群,如图所示。
让我们回到前面的思考题,看看如何通过单节点变更的方法解决成员变更的问题。为了演示方便,我们假设节点A是领导者,如图所示。
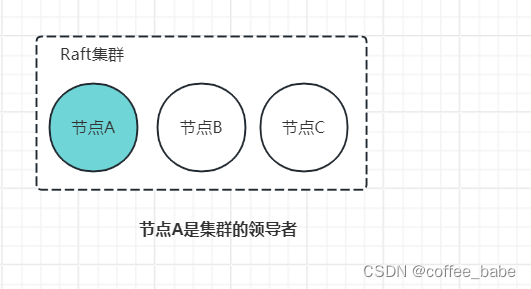
目前的集群配置为【A,B,C】,我们先向集群中加入节点D,这意味着新配置为【A,B,C,D】。具体实现步骤如下:
- 1.第一步,领导者(节点A)向新节点(节点D)同步数据
- 2.第二步,领导者(节点A)将新配置【A,B,C,D】作为一个日志项复制到新配置中的所有节点(节点A、B、C、D)上,然后将新配置的日志项应用到本地状态机,完成单节点变更,如图所示。
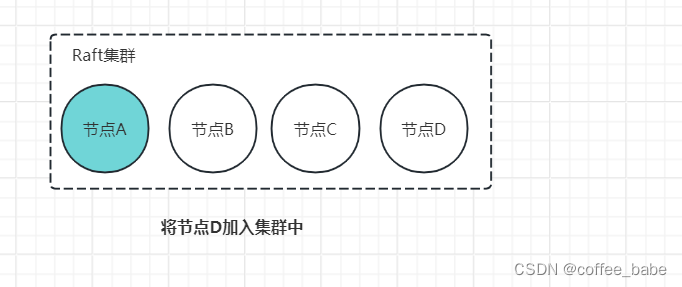
变更完成后,集群配置变为【A,B,C,D】,我们再向集群中加入节点E,也就是说,新配置为【A,B,C,D,E】。具体实现步骤与上面类似。
- 1.第一步,领导者(节点A)向新节点(节点E)同步数据
- 2.第二步,领导者(节点A)将新配置【A,B,C,D,E】作为一个日志项复制到新配置中的所有节点(A、B、C、D、E)上,然后将新配置的日志项应用到本地状态机,完成单节点变更,如图所示。
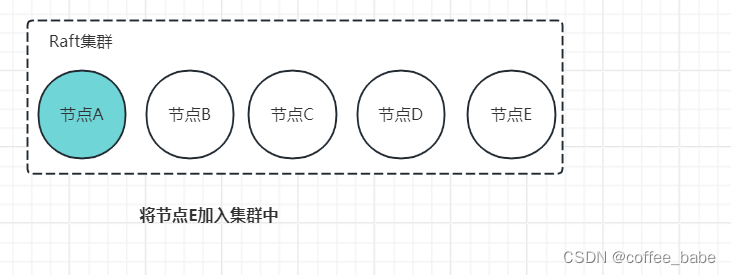
这样一来,我们就通过一次变更一个节点的方式完成了成员变更,保证了集群中始终只有一个领导者,也保证了集群稳定运行,持续提供服务。
在正常情况下,不管旧的集群配置是怎么组成的,旧配置的"大多数"和新配置的"大多数"都会有一个节点是重叠的。也就是说,不会同时存在旧配置和新配置两个"大多数"。
如果你遇到这种情况,可以在领导者启动时创建一个NO_OP日志项(也就是空的日志项),当领导者应用该NO_OP日志项后,再执行成员变更请求。具体实现可参考Hashicorp Raft的源码,也就是runLeader()函数,代码如下:
noop :=&logFuture{
log: Log{
Type:LogNoop,
},
}
r.dispatchLogs([*logFuture{noop}])
当然,有的人会好奇"联合共识",在我看来,联合共识难以实现,很少被Raft算法采用。比如,除了Logcabin外,目前还没有其他常用Raft算法采用这种方式。
注意。
因为联合共识实现起来复杂,所以绝大多数Raft算法采用的都是单节点变更的方法(比如Etcd、Hashicorp Raft),其中,Hashicorp Raft单节点变更的实现是由Raft算法的作者迭戈安加罗(Diego Ongaro)设计的,很有参考价值