01.Android简介
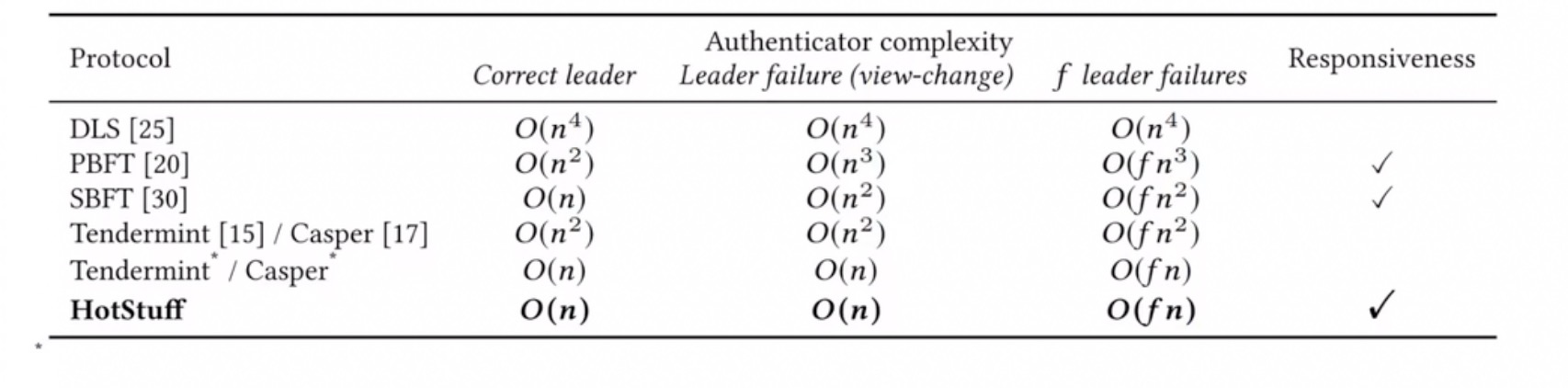
Android(安卓)是一种基于Linux内核(不包含GNU组件)的开源操作系统,最初由安迪·鲁宾开发,主要支持手机。2005年8月由Google收购注资;2007年11月,Google与84家硬件制造商、软件开发商及电信营运商组建开放手机联盟共同研发改良Android系统。随后Google以Apache开源许可证的授权方式,发布了Android的源代码。在开发5年后,全世界采用Android的设备数量就已达到10亿台。下图所示为知名流量检测机构StatCounter统计的2022年9月至2023年2月全球移动操作系统市场份额占比情况,其中Android始终占据全球移动操作系统70%以上的市场份额:
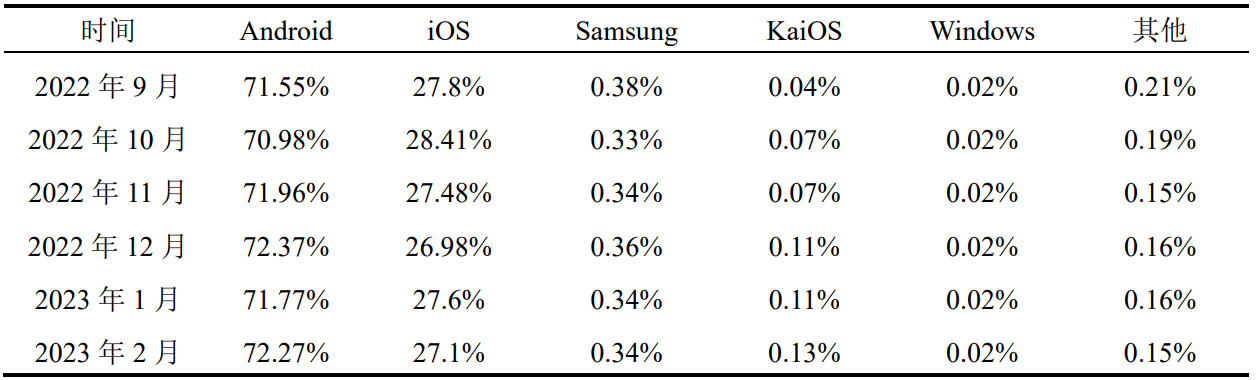
▲全球移动操作系统市场份额占比
Android系统以其开源性、丰富的应用生态系统、硬件兼容性、用户可定制性,广泛应用于智能手机、平板电脑、电视、机器人、汽车等设备。Android在汽车车载系统领域的应用始于2014年,由谷歌牵头与知名汽车制造商联合推出了名为Open Automotive Alliance的新组织。该联盟由谷歌、通用、本田、奥迪、现代和芯片制造商Nvidia组成,专注于将“成功的移动操作系统”以“专为汽车而设计的方式”引入车载娱乐系统,并于当年推出了Android Auto系统(支持将智能手机上的内容传送至汽车屏幕)。发布3年后的2017年,Android系统工程副总裁帕特里克·布雷迪(Patrick Brady)表示,当前支持Android Auto的汽车已达300多款。
02.基于SkyEye运行Android
对于移动设备的开发而言,其软件开发与硬件研制往往是相辅相成的,复杂、耗时、高价的硬件环境搭建经常会成为导致开发滞后的重大阻碍。天目全数字实时仿真软件SkyEye,能够帮助搭建与真实硬件运行速率一致的仿真目标系统,并运行移动设备操作系统,大大改善移动设备操作系统受硬件设备资源制约的困境。
考虑到Android在移动设备操作系统开发中的普遍性,SkyEye早在2012年推出的skyeye-1.3.5版本中就已适配Android,下文将演示基于SkyEye模拟Android的运行过程。
03.实例演示:
Step 1:在Linux系统下安装skyeye-1.3.5版本。
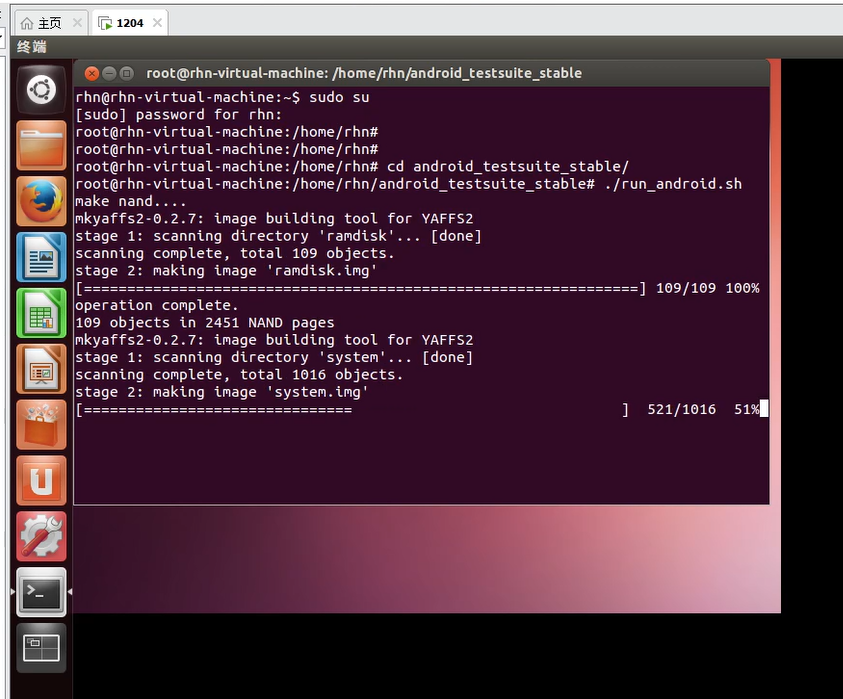
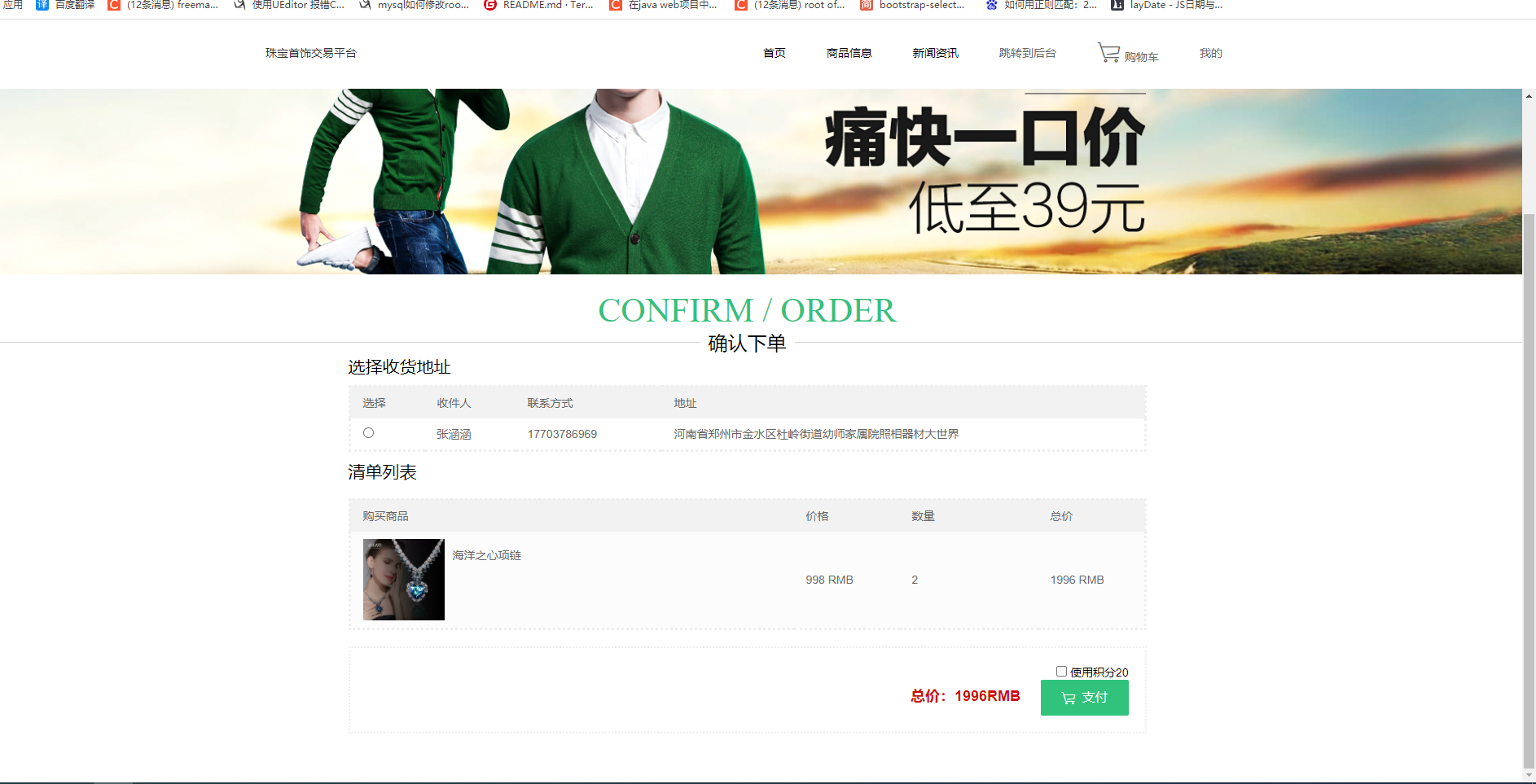
Step 2:进入Android测试用例的文件夹,直接运行用例,即可呈现Android外观界面。

Step 3:可通过运行小游戏测试程序运行情况,这里以“愤怒的小鸟”为例。

Step 4:运行成功,同样证明基于SkyEye运行Android运行成功。