免安装SQL管理工具HeidiSQL

---

一、安装

到官方网址：https://www.heidisql.com/

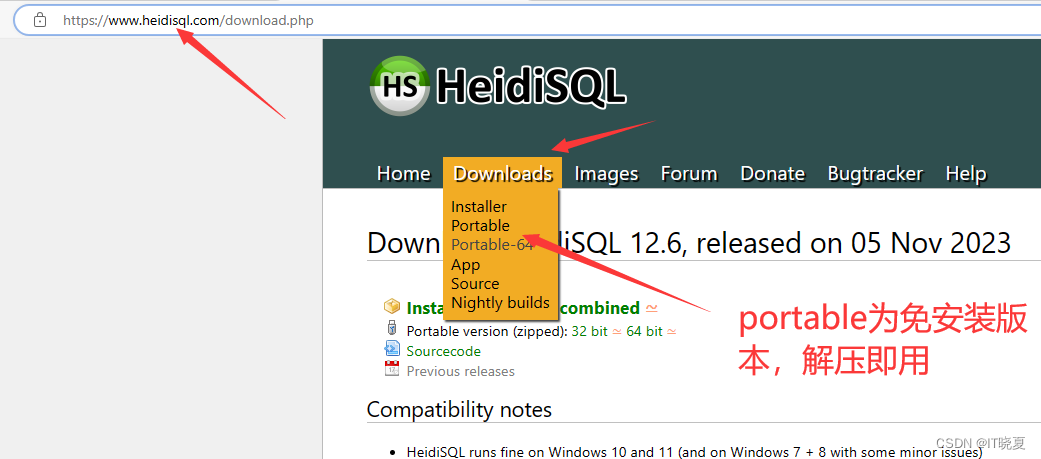
下载后按不同版本安装或解压，运行目录中的heidisql应用程序。
该工具可以对MariaDB, MySQL, Microsoft SQL, PostgreSQL ，SQLite数据库实现可视化的、方便的管理。

二、建库

创建数据库时，工具默认的字符校对（其他工具有时也叫字符集、字符编码)是Latin1_swedish_ci
一般我们都会选择utf8mb4作为多语言的通用字符集支持，但该工具下面有非常多的utf8mb4选项（如图），他们的区别是什么？又如何选择？

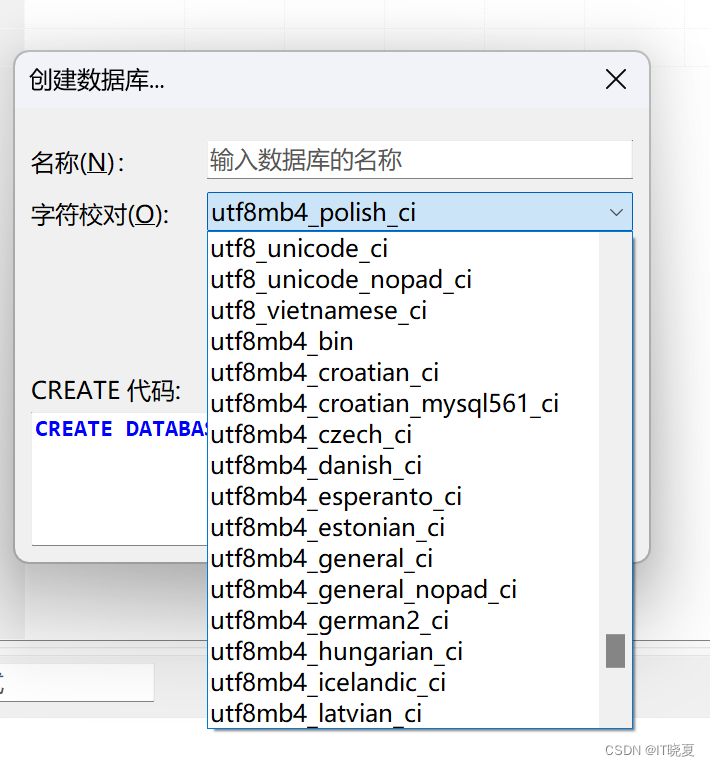
这些字符编码集的命名规则是：

字符集_[编码|语言][_重音][_大小写敏感][_bin]

其中：
字符集： 例如：utf8mb4
编码或者语言：可选，包括0900、unicode、unicode_520或某个特别定制的语言，例如 _thai 泰国
重音：ai 表示不区分重音，as 表示区分重音
大小写敏感： ci 表示不区分大小写，cs 表示区分大小写
如果是：
bin: 采用二进制比较和排序。

**

因此，通常我们选择：

**

• utf8mb4_general_ci——不区分大小写的通用排序规则，适用于多语言环境。
• utf8mb4_bin—— 二进制比较和排序，区分大小写和字符编码

更详细的编码说明参考：https://blog.csdn.net/m0_47406832/article/details/135395392
heidisql工具使用参考：https://blog.csdn.net/qq_29864051/article/details/134018451