片头
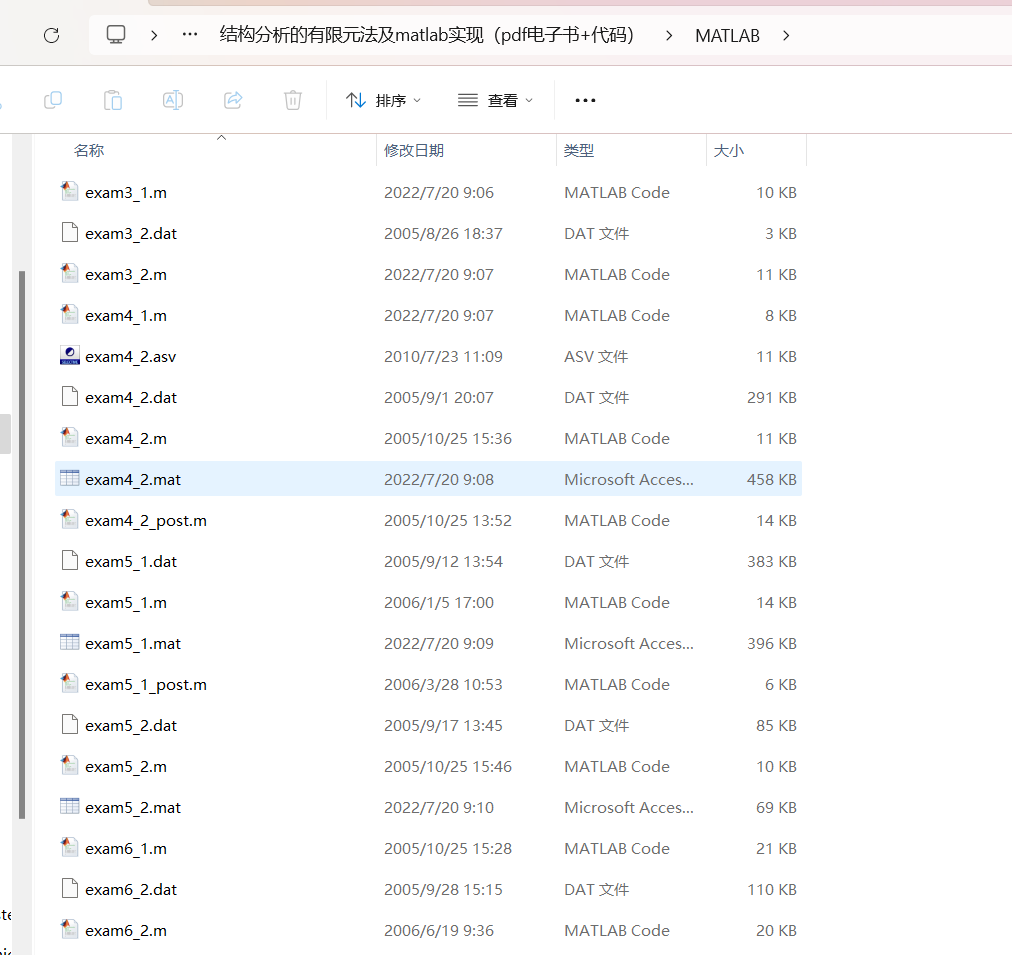
嗨!小伙伴们,大家好!今天我们来深入理解堆这种数据结构,分析一下堆排序以及TOP-K问题,准备好了吗?我要开始咯!

一、堆排序
这里我们先假设要排成升序,也就是从左到右,结点的值依次增大
思路一:①先有堆这个数据结构,②给定一个数组arr, 我们可以把arr数组里面的元素全部拷贝到堆中,然后利用堆自身向下调整算法来进行排序,排成小堆,排好序后,再逐一拷贝回arr数组。
向下调整算法有一个前提:左右子树必须是堆
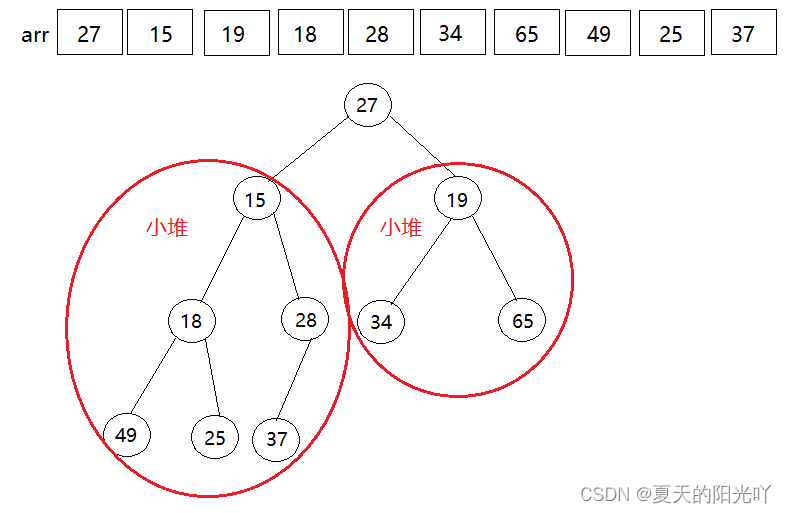
采用向下调整算法,从第一个结点(下标为0)开始,逐个进行比较,如果子节点比父节点大,则交换
第一次:
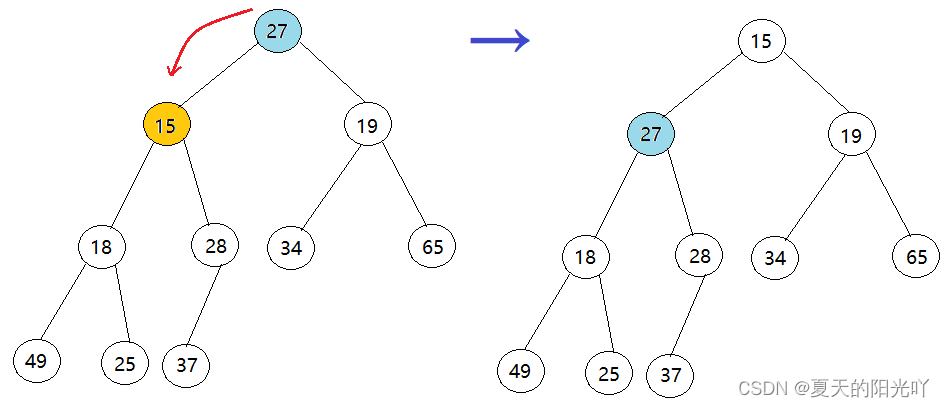
第二次:
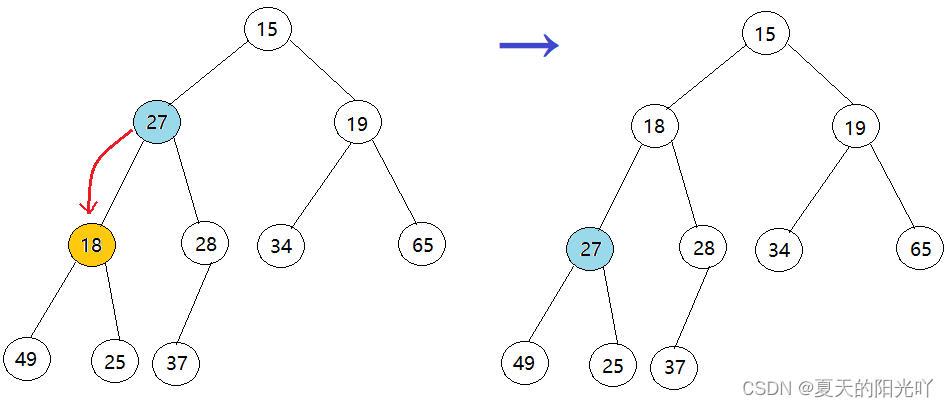
第三次:

好啦,了解完向下调整算法后,那什么是向下调整建堆呢?
举个例子,接下来的内容可要仔细听好咯~

假设我们需要建立大堆,我们可以保持最后一层不动,也就是叶子结点的那一层不变,调整它的上一层,也就是从倒数第一个叶子结点的父节点开始向下调整,比较父节点的左孩子和右孩子,如果孩子结点比父节点大,那么交换,然后比较下一个父节点和它的孩子结点。
第一次:最后一个节点的下标为size-1,那么它的父节点(倒数第一个非叶子结点)的下标为(size-1-1)/2 , 比较父节点的左孩子和右孩子

第二次:从倒数第一个非叶子结点依次往前找父节点,也就是 (size-1-1)/2 -1 ,然后比较它的左孩子和右孩子
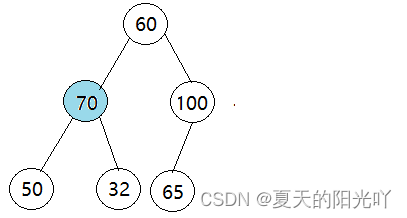
此时我们比较“70”的左孩子“50”和右孩子“32”,发现左右孩子都比父节点的值小,因此我们不作处理,继续往前寻找父节点。
第三次:往前找父节点,也就是 (size-1-1)/2 -1 -1, 我们找到了“60”这个父节点,这里有一个隐藏的细节,不知道大家发现了没:“60”这个结点的左右子树都是大堆,这时,比较它的左孩子“70”和右孩子“100”,发现右孩子"100"比左孩子大,因此将父节点的值和子节点交换。
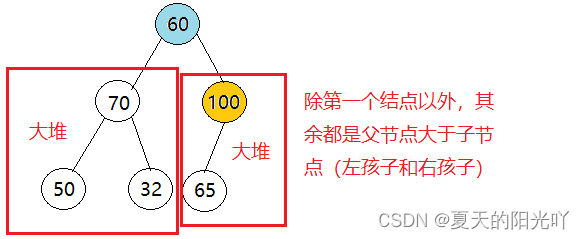

第四次:我们寻找“60”这个父节点的孩子结点,发现它只有左孩子结点,并且左孩子结点的值比父节点大,因此交换
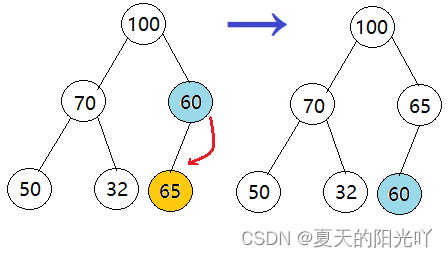
OK啦,我们向下调整建堆就完成啦!
代码如下:
//交换
void Swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
//向下调整算法(小堆)
void AdjustDown(ElemType* arr, int size, int parent) {
assert(arr);
int child = parent * 2 + 1;//假设左孩子比右孩子小
while (child < size)
{ //还没有遍历到叶子结点的时候,进入循环
if (child + 1 < size && arr[child + 1] < arr[child])
{ //如果右孩子存在,并且右孩子的值小于左孩子
child = child + 1;
}
if (arr[child] < arr[parent])
{ //如果子节点小于父节点,交换
Swap(&arr[parent], &arr[child]);
parent = child;//将子节点赋给父节点
child = parent * 2 + 1;//寻找下一个子节点
}
else
{ //如果父节点小于子节点,退出循环
break;
}
}
}
//堆的构建
void HeapCreate(Heap* hp, ElemType* a, int n) {
//断言,防止传入空指针
assert(hp);
//断言,防止传入空指针
assert(a);
//将堆的动态数组arr开辟一个能存放n个元素的空间
hp->arr = malloc(n * sizeof(ElemType));
if (hp->arr == NULL) { //如果内存不足,开辟失败
perror("malloc fail!\n");
exit(1);
}
//将a数组里面的所有元素拷贝到堆的动态数组中
memcpy(hp->arr, a, n * sizeof(ElemType));
//堆的容量为n
hp->capacity = n;
//堆的大小为n
hp->size = n;
//向上调整建堆
//从下标为1的元素开始,一直到下标为size-1的元素结束
/*for (int i = 1; i < hp->size; i++) {
AdjustUp(hp->arr, i);
}*/
//向下调整建堆,将堆里面的所有元素调整成小堆
//从最后一个结点的父节点开始,一直到根节点结束
for (int i = (hp->size-1-1)/2 ; i >= 0; i--) {
AdjustDown(hp->arr, hp->size, i);
}
}
//堆的判空
int HeapEmpty(Heap* hp) {
assert(hp);//断言,防止传入空指针
return hp->size == 0;//判断堆的大小是否为0
}
//取堆顶的数据
ElemType HeapTop(Heap* hp) {
assert(hp);//断言,防止传入空指针
return hp->arr[0];//获取堆顶元素
}
//堆的删除
void HeapPop(Heap* hp) {
assert(hp);//断言,防止传入空指针
Swap(&hp->arr[0], &hp->arr[hp->size - 1]);//将堆顶元素和最后一个元素进行交换
hp->size--;//堆的大小减一
AdjustDown(hp->arr, hp->size, 0);//向下调整算法
}
//堆的销毁
void HeapDestroy(Heap* hp) {
assert(hp);//断言,防止传入空指针
if (hp->arr)
{ //如果堆的动态数组存在,那么就释放占用的内存空间
free(hp->arr);
hp->arr = NULL;//置空
}
hp->capacity = 0;//堆的容量为0
hp->size = 0;//堆的大小为0
}
// 对数组进行堆排序
void HeapSort(int* a, int n) {
assert(a);//断言,防止传入空指针
Heap hp;//创建堆这个结构体
HeapCreate(&hp, a, n);//堆的创建,将数组的元素全部拷贝到堆中,进行堆排序
int i = 0;//数组下标从0开始
while (!HeapEmpty(&hp))
{ //将堆里面的数据依次拷贝到数组中
a[i++] = HeapTop(&hp);
HeapPop(&hp);//每拷贝完一次,堆就删除堆顶元素
}
HeapDestroy(&hp);//堆的销毁,防止内存泄漏
}测试一下:
#include"Heap.h"
int main() {
int arr[] = { 23,45,89,12,33,78,100 };
HeapSort(arr, sizeof(arr) / sizeof(arr[0]));
for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++) {
printf("%d ", arr[i]);
}
return 0;
}运行结果为:
23 45 12 33 78 89 100
思路一理解起来很简单,但是它有2个致命的缺陷:①必须要提供堆这种数据结构!②空间复杂度为O(N) , 那还有没有其他方法呢?
思路二:①直接对数组进行向下调整建堆,先排成大堆 ②再采用交换思想,逐步排成小堆
不过,有一个小问题:我想排成升序,为啥不能直接建小堆呢?
来,咱们举个例子~

我们现在需要获取次小的元素,于是我们把栈顶元素删除

因此,如果要排成升序,只能选择建大堆!
还是arr数组,我们再来画一遍图~ 这次是建大堆,别忘记哈!

我们想要排成升序,该怎么做呢?
很简单~ 我们现在已知最大的元素是“9”,是堆顶元素,下标为0;最小的元素是“0”,是堆底元素,下标为 n-1 (n代表数组arr的个数),我们已知最大元素和最小元素,那么就让它们交换,将最大的元素放在最后

接下来把最后一个数不看作堆里面,也就是说堆里面原本有n个数,现在把最后一个数“9”不看作堆里面,现在一共有n-1个数。然后我们再开始从根节点向下调整,继续调整成大堆。(因为之前已经创建好大堆了,因此不需要从倒数第一个非叶子结点开始向下调整)
第一次:从下标为0的元素开始,比较它的左孩子和右孩子,如果其中一个子节点大于父节点,就进行交换。

第二次:继续比较父节点和它的子节点,如果其中一个子节点大于父节点,就进行交换。

第三次:继续比较父节点和它的子节点,如果其中一个子节点大于父节点,就进行交换。

完整过程如下:

OK,现在我们将剩余的元素又排成了大根堆,我们继续将堆顶元素“8”和堆底元素“4”进行交换~
第一次:

第二次:
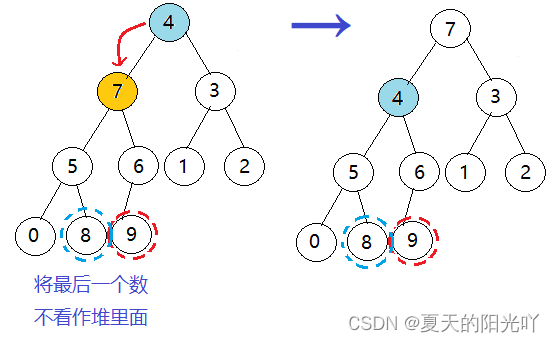
第三次:
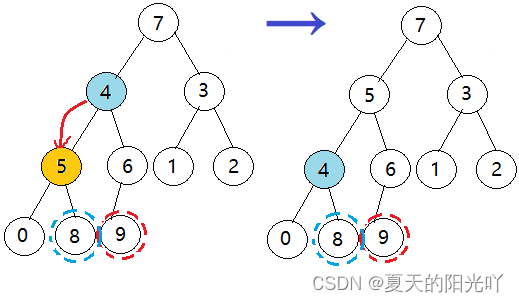
OK,此时已经符合大根堆,也就是堆中每一个父节点都大于子节点,左右子树都是大堆。
完整过程如下:

OK,现在我们将剩余的元素又排成了大根堆,我们继续将堆顶元素“7”和堆底元素“0”进行交换~
后面的过程和前面一样,这里就不画图了~
代码如下:
//交换
void Swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
//向下调整算法(大堆)
void AdjustDown(ElemType* arr, int size, int parent) {
assert(arr);
int child = parent * 2 + 1;//假设左孩子比右孩子大
while (child < size)
{ //还没有遍历到叶子结点的时候,进入循环
if (child + 1 < size && arr[child + 1] > arr[child])
{ //如果右孩子存在,并且右孩子的值大于左孩子
child = child + 1;
}
if (arr[child] > arr[parent])
{ //如果子节点大于父节点,交换
Swap(&arr[parent], &arr[child]);
parent = child;//将子节点赋给父节点
child = parent * 2 + 1;//寻找下一个子节点
}
else
{ //如果父节点大于子节点,退出循环
break;
}
}
}
//堆排序
void HeapSort1(int* a, int n) {
assert(a);//断言,防止传入空指针
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{ //从最后一个结点的父节点开始,一直到根节点结束
AdjustDown(a, n, i);//向下调整算法,调整成大堆
}
//这里的n-1有2层含义:
//①数组最后一个元素的下标为n-1
//②数组总共有n个数,交换后将最后一个值不看作堆里面,共n-1个数
int end = n - 1;
while (end > 0) {
Swap(&a[0], &a[end]);//将首尾元素交换
AdjustDown(a, end, 0);//向下调整算法,从下标为0的元素开始
end--;//每交换完一次,都要把最后一个数不看作堆里面
}
}好啦,堆排序的两种方法讲解完毕,接下来我们继续学习TOP-K问题
二、TOP-K问题
代码如下:
//交换
void Swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
//向下调整算法
void AdjustDown(ElemType* arr, int size, int parent) {
assert(arr);
int child = parent * 2 + 1;//假设左孩子比右孩子小
while (child < size)
{ //还没有遍历到叶子结点的时候,进入循环
if (child + 1 < size && arr[child + 1] < arr[child])
{ //如果右孩子存在,并且右孩子的值小于左孩子
child = child + 1;
}
if (arr[child] < arr[parent])
{ //如果子节点小于父节点,交换
Swap(&arr[parent], &arr[child]);
parent = child;//将子节点赋给父节点
child = parent * 2 + 1;//寻找下一个子节点
}
else
{ //如果父节点小于子节点,退出循环
break;
}
}
}
//文件中找TopK问题
void CreateNDate()
{
// 造数据
int n = 10000;
srand(time(0));//生成随机数
const char* file = "data.txt";
//打开文件
FILE* fin = fopen(file, "w");
if (fin == NULL)
{
perror("fopen error");
return;
}
for (size_t i = 0; i < n; ++i)
{
int x = rand() % 1000000;
fprintf(fin, "%d\n", x);
}
//关闭文件
fclose(fin);
}
void PrintTopK() {
printf("请输入k :>");
int k = 0;
scanf("%d", &k);
//打开文件
const char* file = "data.txt";
FILE* fout = fopen(file, "r");
if (fout == NULL) {
perror("fopen error");
return -1;
}
int* minheap = malloc(sizeof(int) * k);//开辟空间
if (minheap == NULL) //如果空间不足,则开辟失败
{
perror("malloc fail!\n");
return -1;
}
for (int i = 0; i < k; i++) //往堆里面存入数据
{
fscanf(fout,"%d", &minheap[i]);
}
//建k个数据的小堆(倒数第一个非叶子结点开始向下调整)
for (int i = (k - 1 - 1) / 2; i >= 0; i--) {
AdjustDown(minheap, k, i);
}
//读取剩余的数据,比堆顶的值大,就替换它进堆
//将剩余n-k个元素依次与堆顶元素交换,如果比堆顶的值大,就替换它进堆
int x = 0;
while (fscanf(fout, "%d", &x) != EOF) {
if (x > minheap[0]) {
minheap[0] = x;
AdjustDown(minheap, k, 0);//从第一个结点开始向下调整
}
}
for (int i = 0; i < k; i++) {
printf("%d ", minheap[i]);
}
fclose(fout);
fout = NULL;
}
int main(){
PrintTopk();
return 0;
}片尾
今天我们学习了堆排序以及堆的TOP-K问题,希望看完这篇文章能对友友们有所帮助!!!
求点赞收藏加关注! ! !
谢谢大家! ! !

![JSP简介——[JSP]1](https://img-blog.csdnimg.cn/direct/4e8a23fd4dd94eb48de2fe48f7c8da70.png)