原数据

import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import metrics### 数据抽取,读⼊数据
df = pd.read_csv("customers1997.csv") #相对路径读取数据
print(df.info())
print(df.columns)
print(df.describe())
# 特征选择,选择RFM
df = df.drop(labels=['customer_id','country','education','gender','member_card','total_children'],axis=1)一、 K-means聚类
1. K-means聚类
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
kmeans = KMeans(n_clusters=4) #构造聚类模型,划分为 4 类
kmeans.fit(df) # 聚类
pre_y = kmeans.predict(df) # 预测点在哪个聚类中,或者是直接采用 kmeans.labels_ 提取
print(pre_y) # 输出每个样本的聚类标签from sklearn import metrics
print("轮廓系数:",metrics.silhouette_score(df, pre_y,metric='euclidean'))
# print("轮廓系数:",metrics.silhouette_score(df, kmeans.labels_,metric='euclidean'))2. 轮廓系数

轮廓系数取值范围[-1,1]
- -1的效果最差
- 1 的效果最好
二、分箱法分类
1. 分类
数据分析--客户价值分析RFM(分箱法/标准化)-CSDN博客
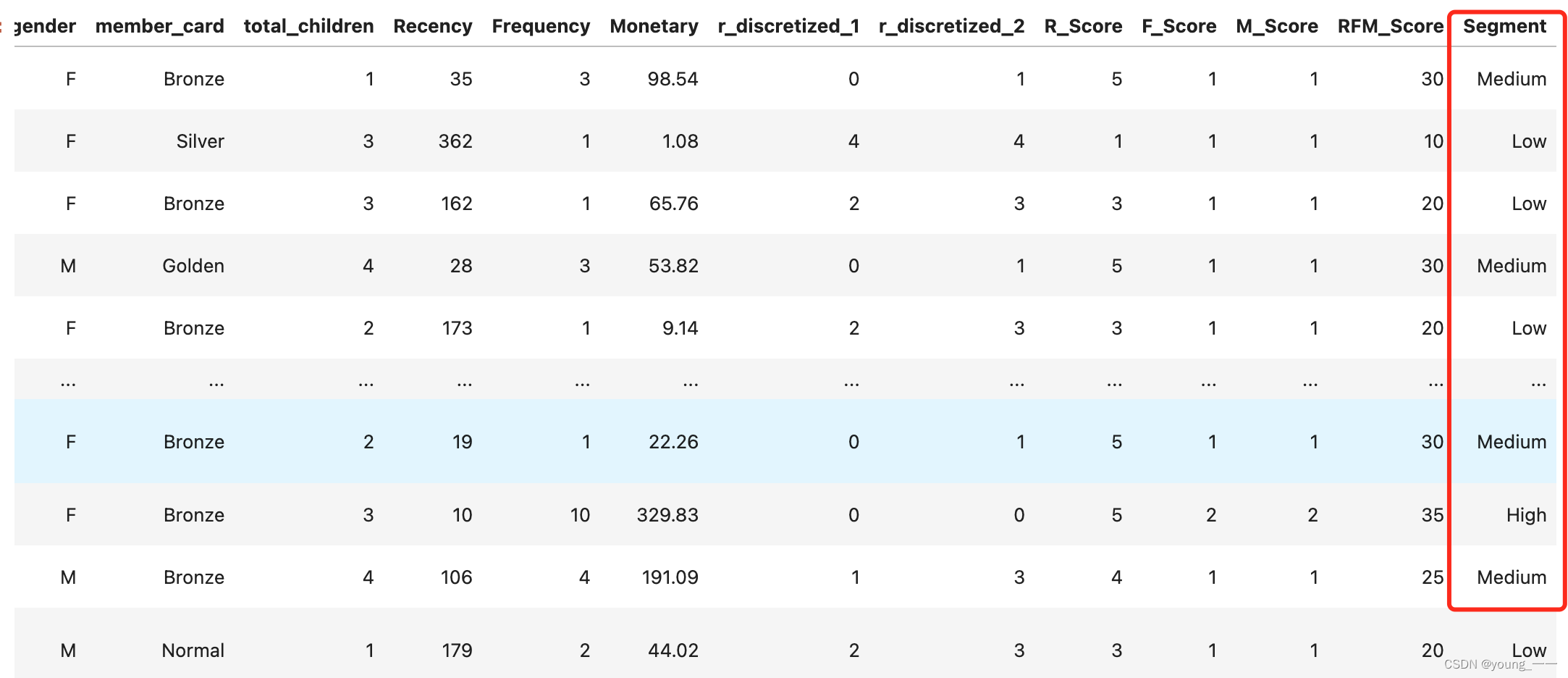
2.轮廓系数
from sklearn import metrics
df_rfm = df[['Recency','Frequency', 'Monetary']]
print("轮廓系数:",metrics.silhouette_score(df_rfm, df['Segment'],metric='euclidean'))
Python——Kmeans聚类算法、轮廓系数(算法理论、代码)_python kmeans-CSDN博客