超越数据的确定性：通过概率主成分分析拥抱不确定性

原文地址：beyond-determinism-in-data-embracing-uncertainty-with-probabilistic-principal-component-analysis

2024 年 4 月 24 日

主成分分析法（Principal Component Analysis，PCA）是一种统计方法，它可以通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，这组变量称为主成分。主成分分析的目标是在数据中找到方差最大的方向，并将这些方向作为新的坐标轴，以最大的保留数据的方差信息。具体来说，PCA通过以下步骤实现：
1. 数据标准化：为了消除不同变量间的量纲影响，首先需要对数据进行标准化处理。
2. 计算协方差矩阵：协方差矩阵描述了数据中各变量间的相关性。
3. 计算特征值和特征向量：通过对协方差矩阵进行特征分解，找到其特征值和对应的特征向量。
4. 选择主成分：根据特征值的大小，选择最大的几个特征值对应的特征向量作为主成分。
5. 形成新的数据集：将原始数据投影到选取的主成分上，形成新的数据集。
主成分分析法在数据降维、信号处理、图像处理等领域有广泛的应用。通过PCA，可以去除数据中的噪声和冗余信息，简化数据的复杂性，同时尽可能保留原始数据的信息量。

介绍

在现代工业数据驱动的环境中，在承认固有数据不确定性的同时有效降低维度的能力可能会产生重大影响。这就是概率主成分分析 (PPCA) 作为强大的统计工具的闪光点，它通过结合概率框架来增强传统主成分分析 (PCA) 的功能。

背景

概率主成分分析（PPCA）是一种统计技术，它扩展了经典的主成分分析（PCA）方法。PCA 试图找到一组能解释数据中最大方差的正交方向（主成分），而 PPCA 则整合了一个概率框架，允许对观测数据和相关不确定性进行建模。

PPCA 将数据 X 建模为由低维潜在变量 Z 加上一些噪声生成。数据生成过程可描述为

xi=Wzi+μ+ϵ

这里，ϵW 是载荷或权重矩阵，? 是数据的平均值，zi 是与第 i 个数据点相关的潜变量，ϵ 代表高斯噪声。

PCA 对数据进行确定性分解，而 PPCA 则不同，它为潜变量 Z 和噪声ϵ 建立了一个概率模型。通常，噪声被假定为各向同性的高斯噪声：

ϵ∼N(0,σ2I)

潜变量也假设为高斯分布：

zi∼N(0,I)

W、σ2 和 ?μ 通常通过最大似然法估算。由于期望最大化（EM）算法能有效处理模型的潜在变量结构，因此经常被用于此目的。

与 PCA 相比的优势

不确定性建模： PPCA 可量化数据表示中的不确定性，更清晰地显示主成分的稳健性。
处理缺失数据： PPCA 可以自然地处理数据中的缺失值，这对标准 PCA 来说是一个挑战。
灵活性：概率框架可以通过各种方式进行扩展，例如为噪声或潜在变量整合不同的分布。

了解 PPCA

PPCA 的核心是通过引入一个用于降维的概率模型来扩展 PCA。这种方法将观察到的数据建模为来自低维度潜空间的数据，再加上一些附加的高斯噪声。它假定每个观测数据点 xi 都是通过线性变换 W 从潜在变量 zi 生成的，并经过平均值 μ 的调整和噪声 ϵ 的扰动。这种噪声被假定为各向同性的高斯噪声，从而使该方法对现实世界中的数据异常具有鲁棒性，而现实世界中的数据异常往往是有噪声和不完整的。

实践中的优势

处理缺失数据： PPCA 最实用的优势之一是其处理缺失数据的能力。传统的 PCA 只有在面对缺失数据点时才会使用估算法，这可能会带来偏差。相比之下，PPCA 可以使用 EM（期望最大化）算法估计缺失值，作为算法执行的一部分。这一功能在生物信息学和社会科学等领域尤为有用，因为在这些领域中，缺失数据是共享的，如果处理不当，可能会使结果出现偏差。
量化不确定性： PPCA 可对其提供的数据表示的不确定性进行估计。这对于数据分析师和科学家来说至关重要，因为他们需要了解预测和分析得出的主成分的可靠性。在金融和天气预报等领域，决策在很大程度上取决于对预测的信心，而 PPCA 能提供更细致入微、更有信心意识的见解。
灵活性和扩展性： PPCA 的概率框架允许各种扩展。例如，它可以根据应用的具体要求进行调整，以纳入不同的噪声分布或对潜变量进行不同的建模。这种灵活性使 PPCA 成为一种通用工具，可适应各种数据集和分析要求。

PPCA 的实际应用

生物信息学：在生物信息学中，PPCA 可用于分析遗传数据，因为测量过程会引入噪声，而且数据往往不完整。通过比传统方法更有效地处理不完整数据，PPCA 可帮助识别导致疾病的潜在遗传因素。
金融：金融数据分析是 PPCA 极其有用的另一个领域。股票市场数据通常不完整且噪声较大，使用 PPCA 可以更好地分析这些数据，从而找出影响市场走势的潜在因素。这有助于制定更稳健的风险管理和投资策略。
图像处理：在图像处理中，特别是在人脸识别和图像压缩等任务中，PPCA 可以更有效地处理不同的光照条件、遮挡和损坏的数据元素。这种适应性提高了图像重建的质量和分析的准确性。

代码

下面，我将提供一个在合成数据集上使用概率主成分分析（PPCA）的完整 Python 代码块。代码将包括数据生成、特征工程、超参数调整、交叉验证、评估指标和结果可视化。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.metrics import explained_variance_score
from sklearn.pipeline import Pipeline
# Generating synthetic data
np.random.seed(42)
true_latent_dim = 2
n_samples = 300
noise_level = 0.1
# True latent variables
Z = np.random.normal(size=(n_samples, true_latent_dim))
W = np.random.uniform(low=-2, high=2, size=(true_latent_dim, 10))  # Weight matrix
mu = np.random.uniform(low=-1, high=1, size=10)  # Mean of the data
X = Z.dot(W) + mu + np.random.normal(scale=noise_level, size=(n_samples, 10))
# Feature scaling
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# Splitting the dataset into training and testing sets
X_train, X_test = train_test_split(X_scaled, test_size=0.2, random_state=42)
# PCA Pipeline and hyperparameter tuning
pipeline = Pipeline([
    ('pca', PCA())
])
param_grid = {
    'pca__n_components': range(1, 6)  # Testing different numbers of components
}
grid_search = GridSearchCV(pipeline, param_grid, cv=5, scoring='explained_variance')
grid_search.fit(X_train)
# Best model
best_model = grid_search.best_estimator_
# Prediction and metrics
X_train_pca = best_model.transform(X_train)
X_test_pca = best_model.transform(X_test)
explained_variance = explained_variance_score(X_test, best_model.inverse_transform(X_test_pca))
print(f"Best number of components: {grid_search.best_params_['pca__n_components']}")
print(f"Explained Variance on Test Set: {explained_variance}")
# Plotting the results
plt.figure(figsize=(12, 6))
if X_train_pca.shape[1] > 1:
    plt.subplot(1, 2, 1)
    plt.scatter(X_train_pca[:, 0], X_train_pca[:, 1], c='blue', alpha=0.5, label='Train')
    plt.scatter(X_test_pca[:, 0], X_test_pca[:, 1], c='red', alpha=0.5, label='Test')
    plt.xlabel('Principal Component 1')
    plt.ylabel('Principal Component 2')
else:
    plt.subplot(1, 2, 1)
    plt.scatter(X_train_pca[:, 0], np.zeros_like(X_train_pca[:, 0]), c='blue', alpha=0.5, label='Train')
    plt.scatter(X_test_pca[:, 0], np.zeros_like(X_test_pca[:, 0]), c='red', alpha=0.5, label='Test')
    plt.xlabel('Principal Component 1')
    plt.yticks([])
plt.title('PCA Projection')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(np.cumsum(best_model.named_steps['pca'].explained_variance_ratio_))
plt.xlabel('Number of Components')
plt.ylabel('Cumulative Explained Variance')
plt.title('Explained Variance Ratio')
plt.tight_layout()
plt.show()

说明

数据生成：我们使用真实潜在空间创建合成数据集，并添加高斯噪声。
特征工程：对数据集进行标准缩放，对特征进行归一化处理。
建立模型：建立 PCA 管道。GridSearchCV 用于根据解释的方差找到主成分的最佳数量。
交叉验证：使用 5 倍交叉验证来评估 PCA 模型的性能。
指标：使用解释方差得分对模型进行评估，解释方差得分可量化主成分在测试数据中所占的方差比例。
曲线图：结果包括 PCA 投影的散点图和显示累积解释方差比的折线图，以解释附加成分对解释方差的贡献。

该代码提供了全面的分析，使 PCA 在保留信息的同时降低维度的有效性得到评估和可视化。

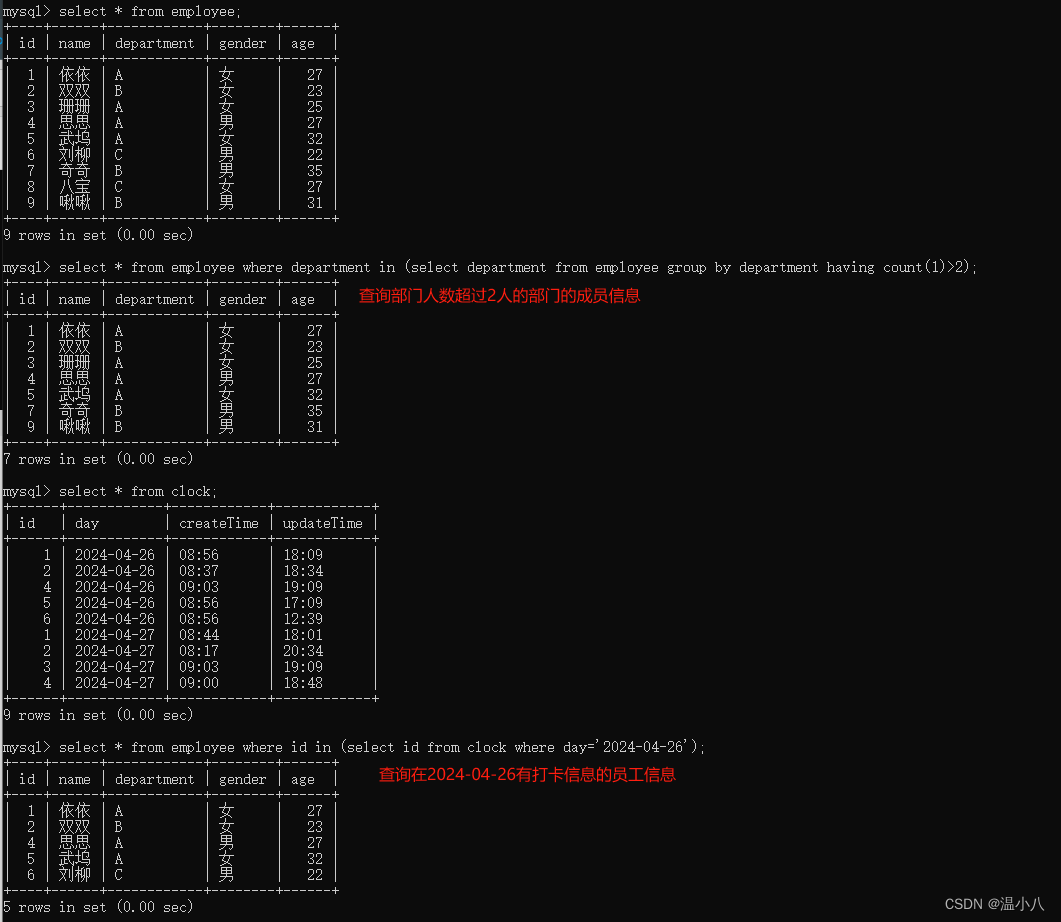
在 PCA 分析中，确定的最佳分量数为一个，该图是投影到第一个主分量上的数据的可视化图。这表明，PCA 发现单个分量足以捕捉数据中的大部分方差。

测试集的解释方差约为 0.549，这意味着测试数据中约 54.9% 的方差可以用这个单一的主成分来解释。这是一个适中的解释方差，意味着虽然主成分捕捉到了一半以上的方差，但数据中仍有很大一部分方差是主成分无法解释的。

Best number of components: 1
Explained Variance on Test Set: 0.5490705019396915

根据具体情况和领域，0.549 的解释方差可能是可以接受的。对于某些应用，捕捉到一半以上的方差可能就足以实现分析目标。而对于其他应用，尤其是信息缺失成本较高的应用，这可能并不令人满意，因此可能需要考虑其他方法或更复杂的模型。

值得注意的是，PCA 是一种线性技术，如果数据具有非线性关系，PCA 可能无法捕捉到所有相关结构。在这种情况下，我们可以探索非线性降维技术，如 t-SNE、UMAP 或自动编码器，可能会捕捉到更多的数据方差。

结论

概率主成分分析是数据分析领域的一大进步，它提供了一种复杂的工具，承认并纳入了真实世界数据固有的不确定性。随着各行各业继续朝着更加以数据为中心的方向发展，概率主成分分析的实际应用可能会不断扩大，为各个领域提供更强大、可靠和细致入微的洞察力。因此，采用概率主成分分析法可以增强数据科学家和分析师的工具包，使各行业能够在深入了解数据的基础上做出更明智的决策。