1、创建向量、矩阵

在R中,c()函数用于创建向量或组合数据对象。它在某些情况下可能会被省略,因为R有一些隐式的向量创建规则。例如,当你使用:操作符创建一个数字序列时,R会自动创建一个向量,所以你不需要显式地调用c()函数。
例如,a = 1:9就是一个隐式调用c()函数的例子,它创建了一个包含1到9的整数序列的向量。而在某些情况下,你可能需要显式地使用c()函数来组合元素,例如当你想要手动创建一个包含不连续元素的向量时,就需要使用c()函数了,比如 b = c(1, 3, 5, 7, 9)。
结果
默认竖着s型填充
2、矩阵运算
运算结果


setwd("E:/adstats") #设置自定义工作目录E:/adstats
source('msaR.R') #加载自定函数
# 第2章 多元数据的数学表达 ---------------------
## —— 2.3 数据矩阵及R表示 ----
#### 创建一个向量
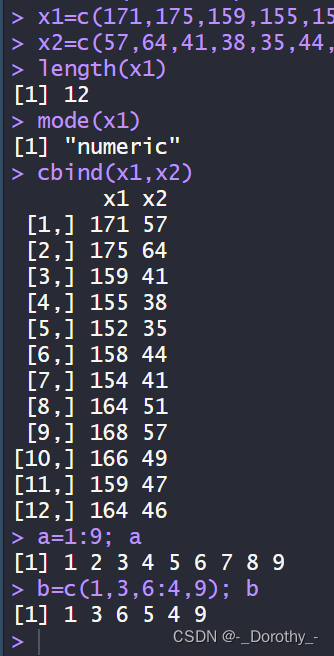
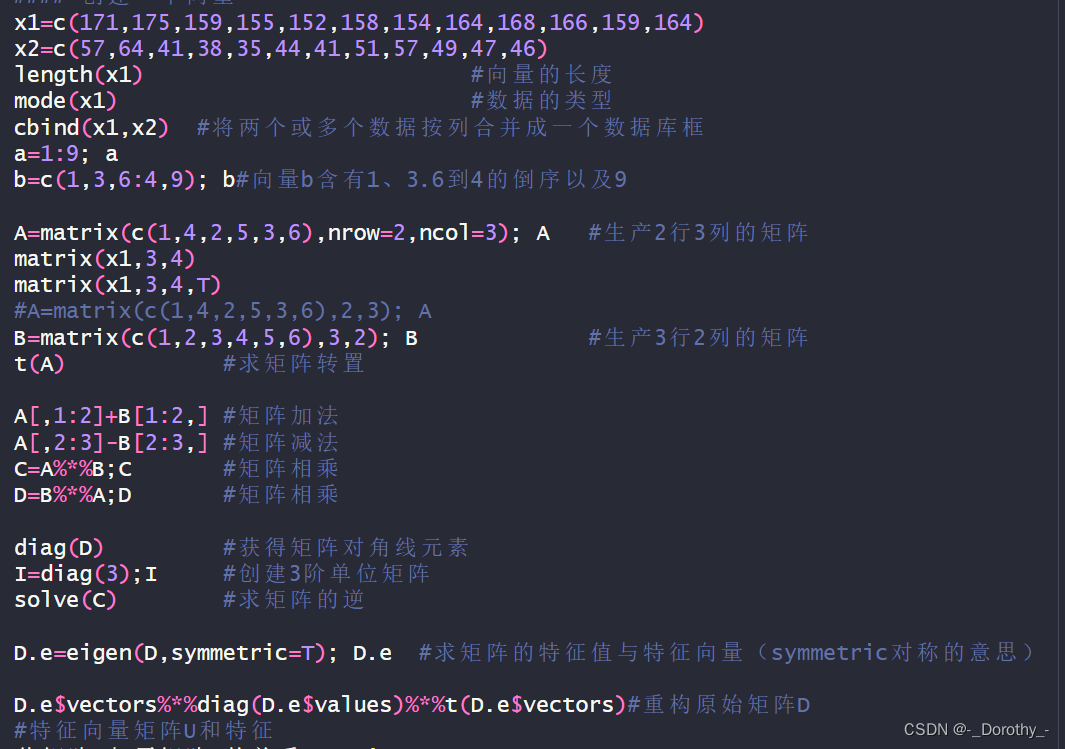
x1=c(171,175,159,155,152,158,154,164,168,166,159,164)
x2=c(57,64,41,38,35,44,41,51,57,49,47,46)
length(x1) #向量的长度
mode(x1) #数据的类型
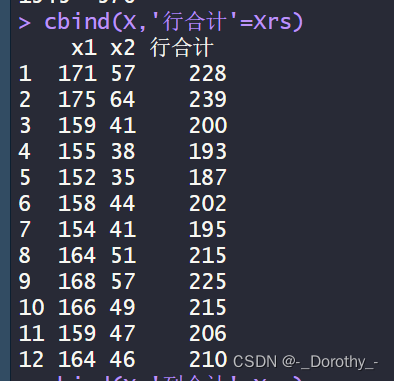
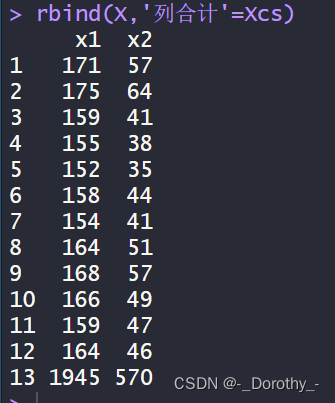
cbind(x1,x2) #将两个或多个数据按列合并成一个数据库框
a=1:9; a
b=c(1,3,6:4,9); b#向量b含有1、3.6到4的倒序以及9
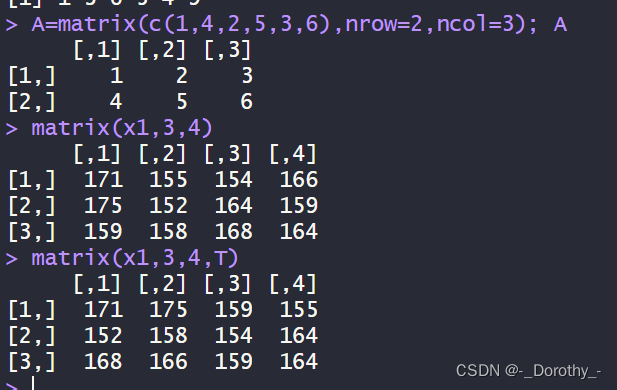
A=matrix(c(1,4,2,5,3,6),nrow=2,ncol=3); A #生产2行3列的矩阵
matrix(x1,3,4)
matrix(x1,3,4,T)
#A=matrix(c(1,4,2,5,3,6),2,3); A
B=matrix(c(1,2,3,4,5,6),3,2); B #生产3行2列的矩阵
t(A) #求矩阵转置
A[,1:2]+B[1:2,] #矩阵加法
A[,2:3]-B[2:3,] #矩阵减法
C=A%*%B;C #矩阵相乘
D=B%*%A;D #矩阵相乘
diag(D) #获得矩阵对角线元素
I=diag(3);I #创建3阶单位矩阵
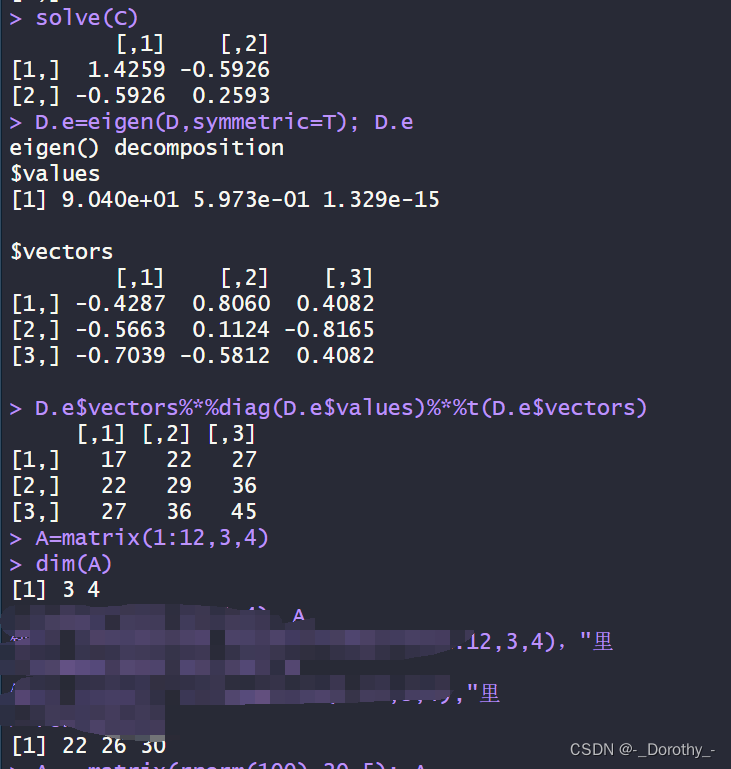
solve(C) #求矩阵的逆
D.e=eigen(D,symmetric=T); D.e #求矩阵的特征值与特征向量(symmetric对称的意思)
D.e$vectors%*%diag(D.e$values)%*%t(D.e$vectors)#重构原始矩阵D
#特征向量矩阵U和特征
值矩阵D与原矩阵A的关系A=UDV'
#(A.c=chol(A)) #矩阵的Choleskey分解
#t(A.c)%*%A.c #Choleskey分解矩阵V与原矩阵A.c的关系A.c=V'V
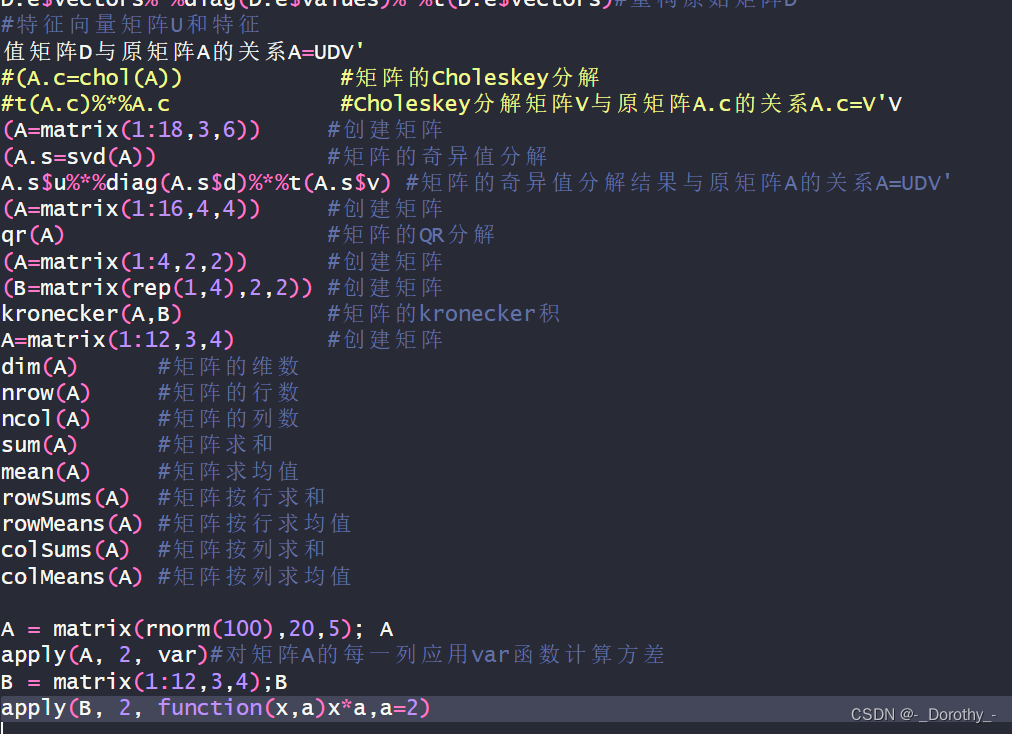
(A=matrix(1:18,3,6)) #创建矩阵
(A.s=svd(A)) #矩阵的奇异值分解
A.s$u%*%diag(A.s$d)%*%t(A.s$v) #矩阵的奇异值分解结果与原矩阵A的关系A=UDV'
(A=matrix(1:16,4,4)) #创建矩阵
qr(A) #矩阵的QR分解
(A=matrix(1:4,2,2)) #创建矩阵
(B=matrix(rep(1,4),2,2)) #创建矩阵
kronecker(A,B) #矩阵的kronecker积
A=matrix(1:12,3,4) #创建矩阵
dim(A) #矩阵的维数
nrow(A) #矩阵的行数
ncol(A) #矩阵的列数
sum(A) #矩阵求和
mean(A) #矩阵求均值
rowSums(A) #矩阵按行求和
rowMeans(A) #矩阵按行求均值
colSums(A) #矩阵按列求和
colMeans(A) #矩阵按列求均值
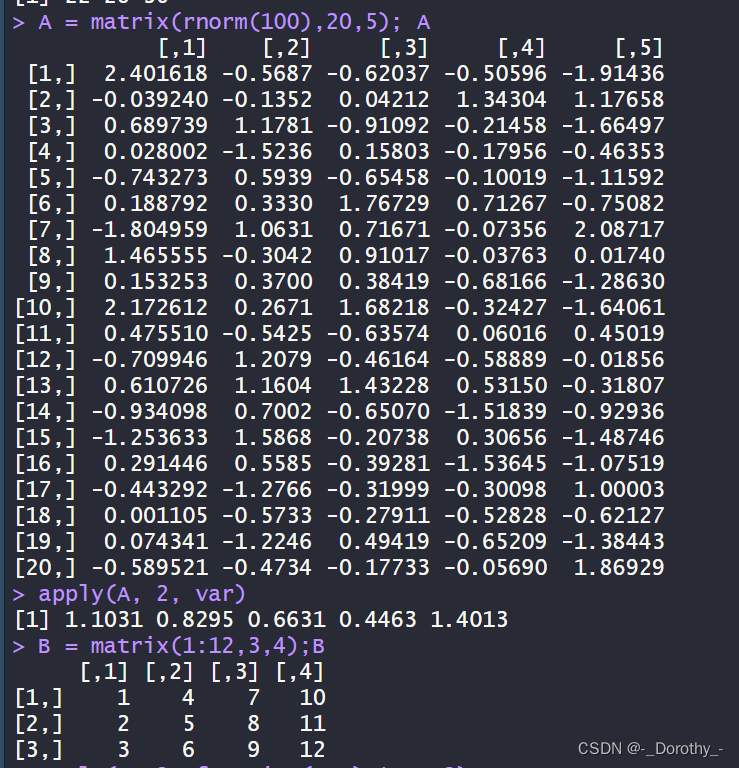
A = matrix(rnorm(100),20,5); A
apply(A, 2, var)#对矩阵A的每一列应用var函数计算方差
B = matrix(1:12,3,4);B
apply(B, 2, function(x,a)x*a,a=2)
3、数据框合并

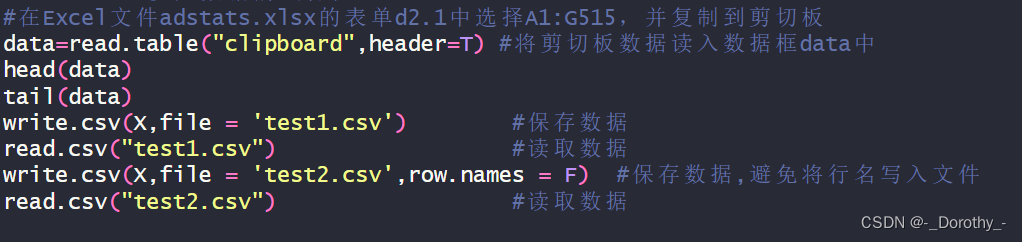
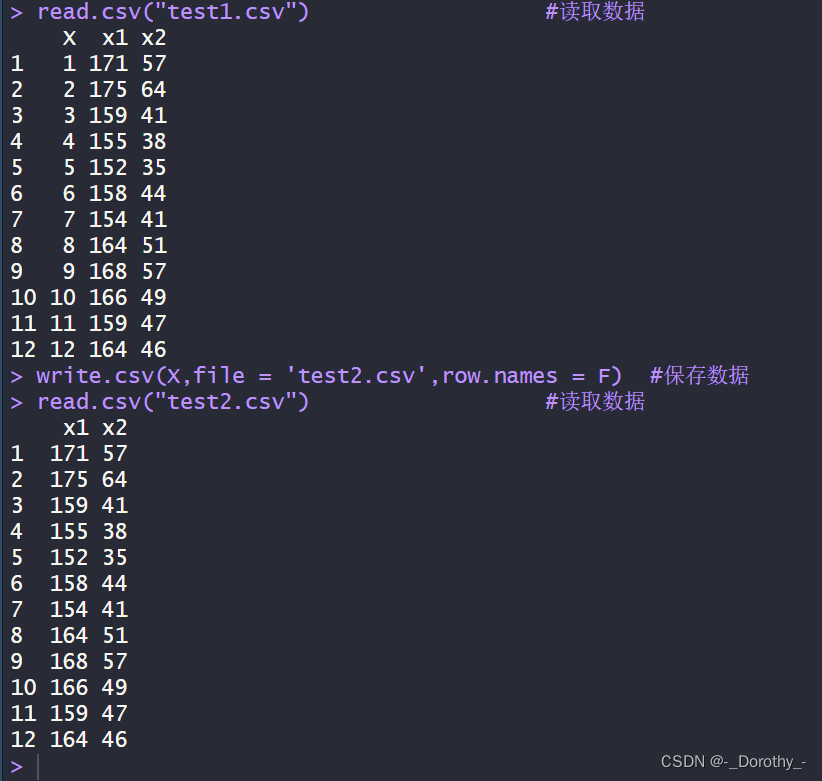
4、将剪切板的数据读入、将数据框写入csv文件
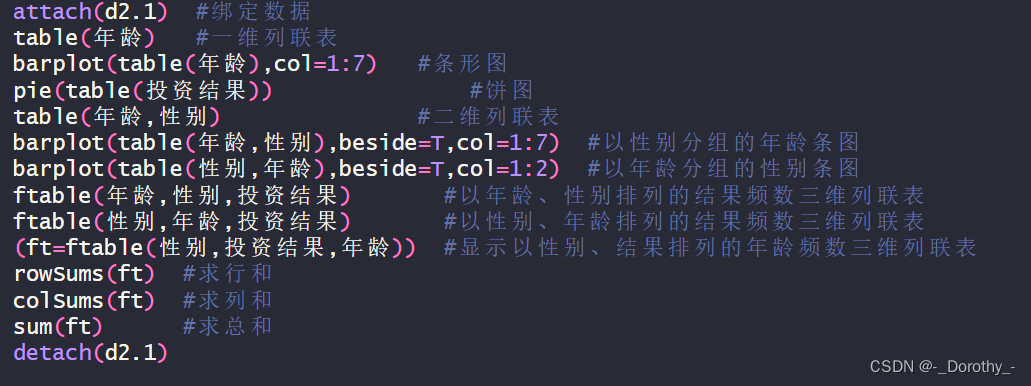
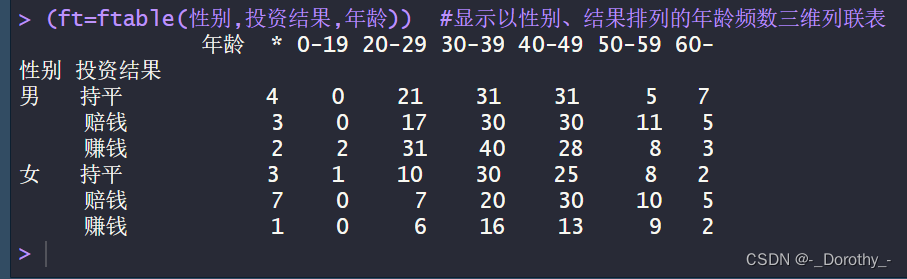
5、条形图、饼图、列联表
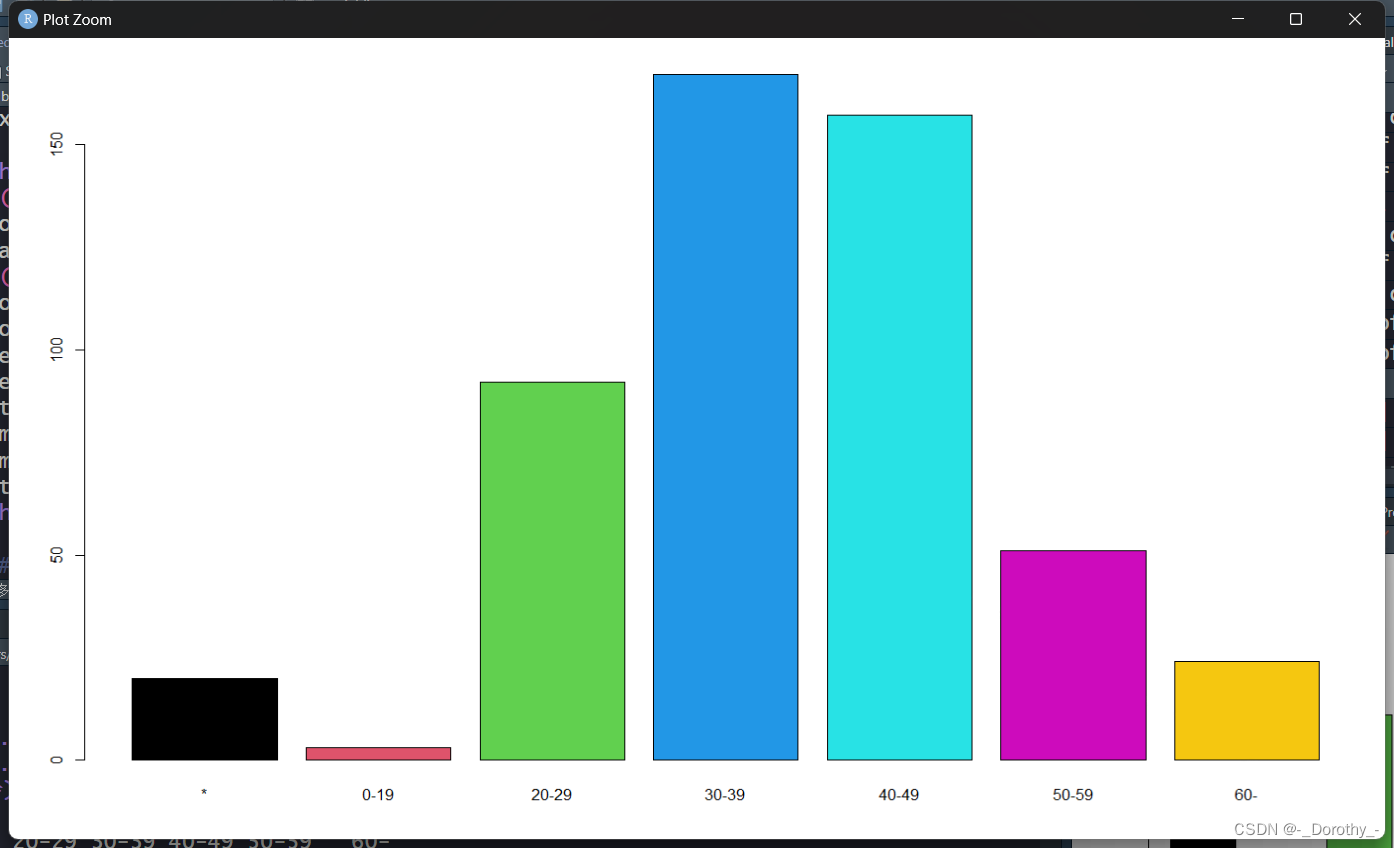
以上代码中所有图如下所示
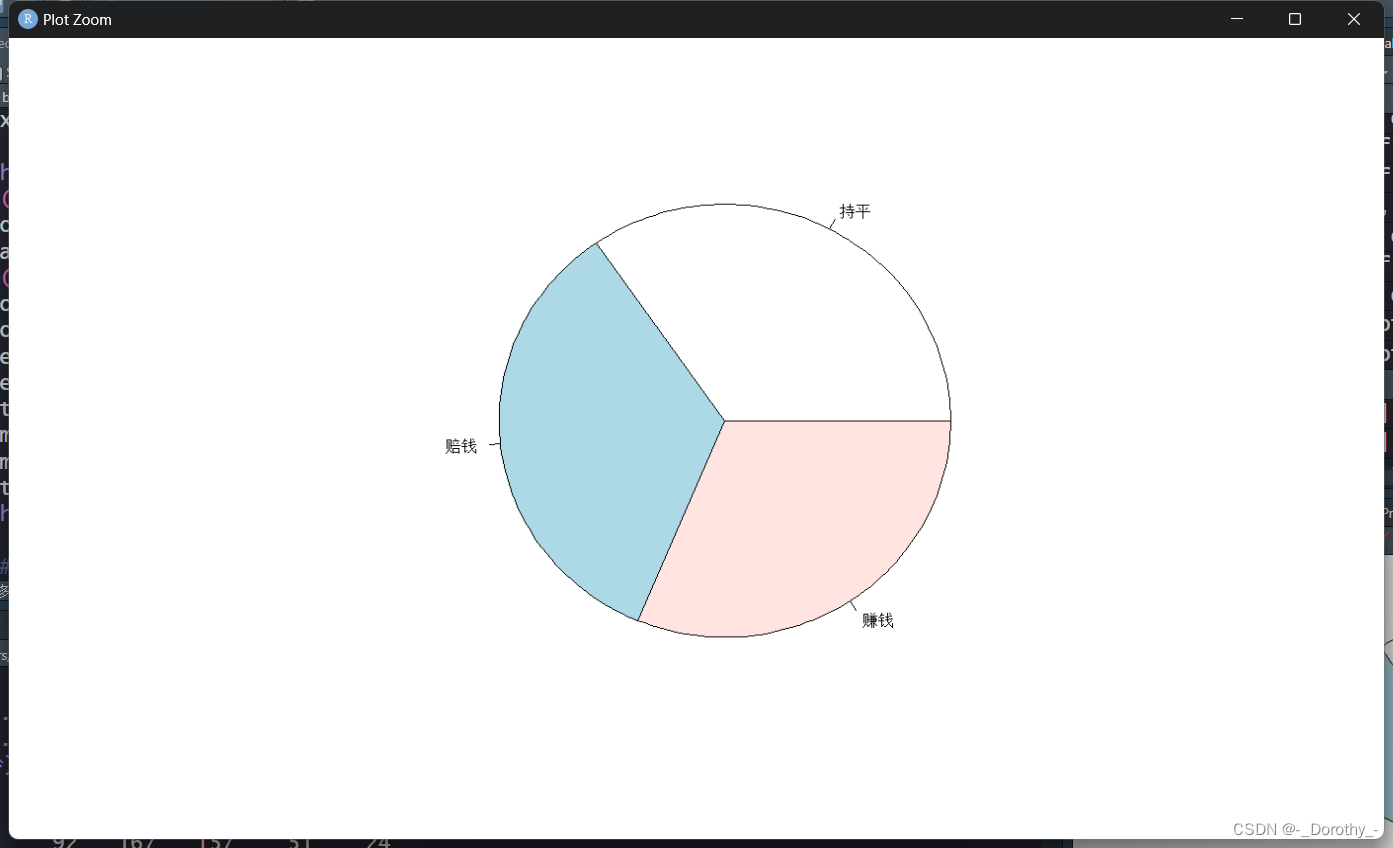
绑定数据的目的和作用
attach(d2.1)是R编程中的一个命令,用于将名为d2.1的数据框绑定到搜索路径上。这意味着可以直接引用d2.1的列,而无需每次都指定数据框。
数据绑定的目的是简化编码,使其更易读,减少对数据框的重复引用。但是,务必谨慎使用,以避免潜在的冲突或混淆,特别是在较大的项目中。
6、多元数据的基本统计分析
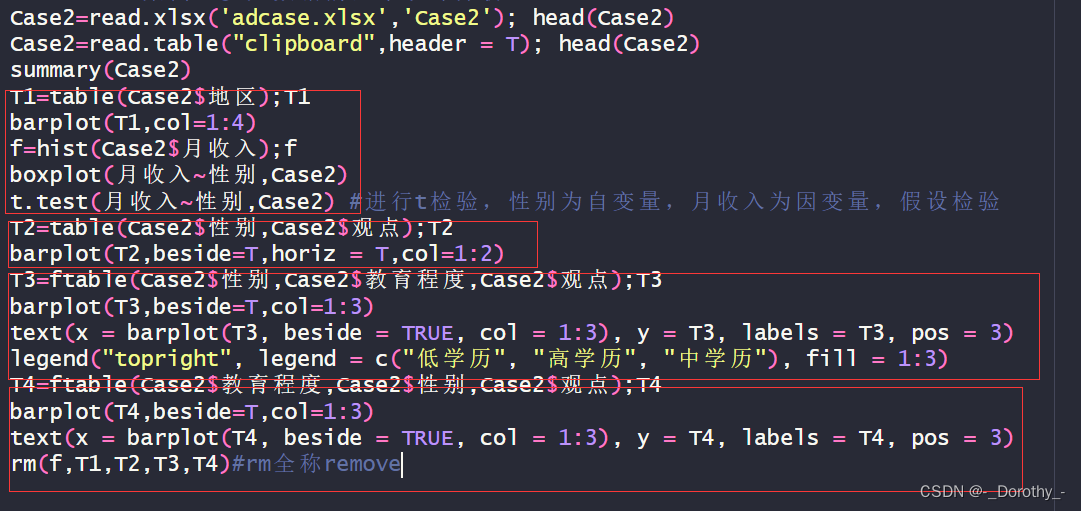
Case2=read.xlsx('adcase.xlsx','Case2'); head(Case2)
Case2=read.table("clipboard",header = T); head(Case2)
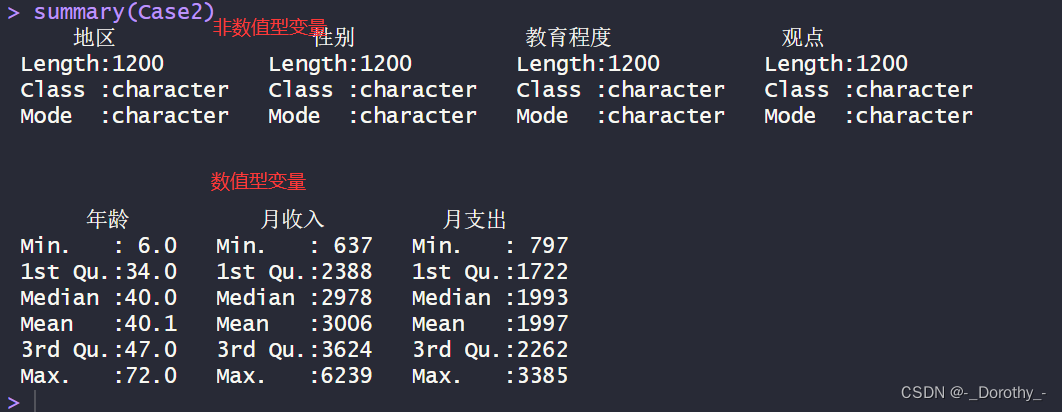
summary(Case2)
T1=table(Case2$地区);T1
barplot(T1,col=1:4)
f=hist(Case2$月收入);f
boxplot(月收入~性别,Case2)
t.test(月收入~性别,Case2) #进行t检验,性别为自变量,月收入为因变量,假设检验
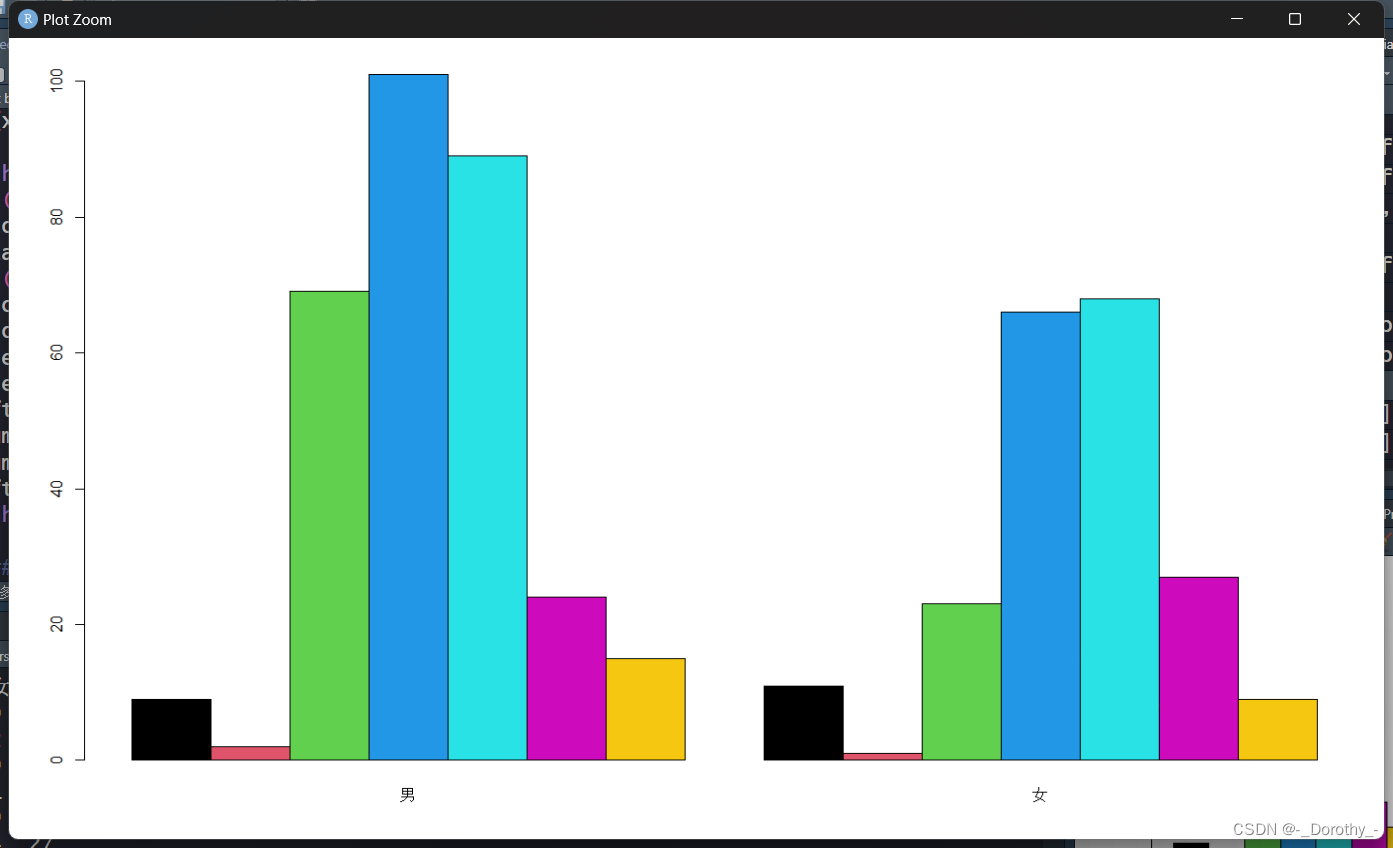
T2=table(Case2$性别,Case2$观点);T2
barplot(T2,beside=T,horiz = T,col=1:2)
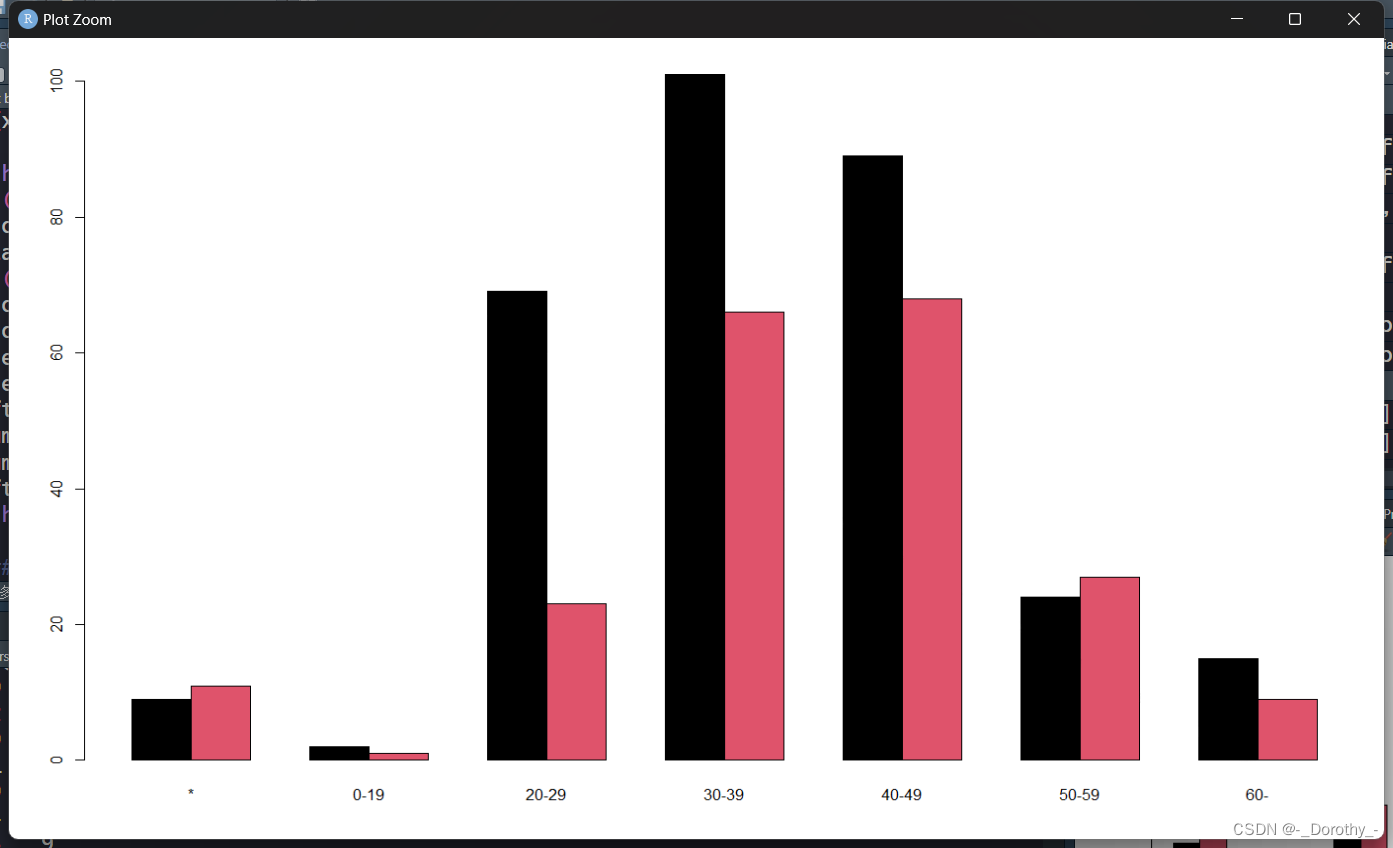
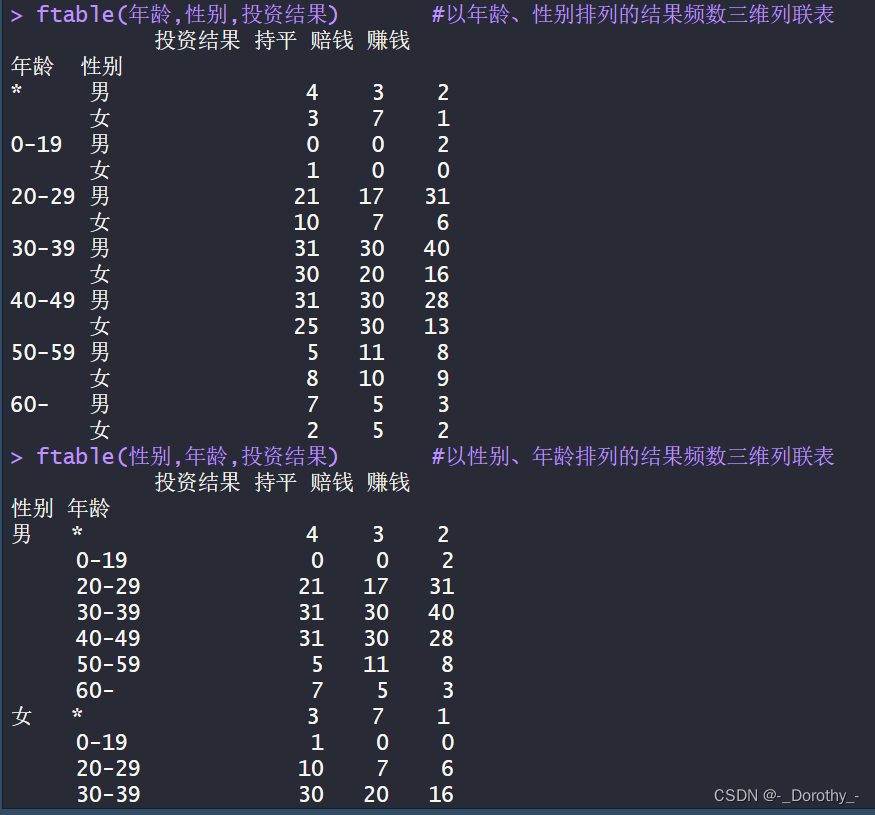
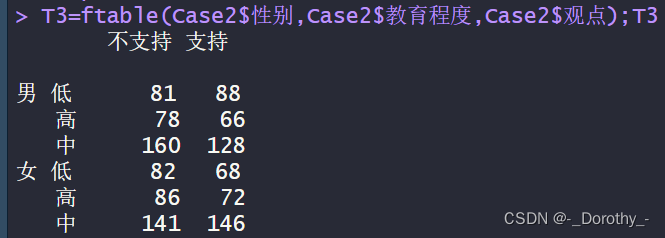
T3=ftable(Case2$性别,Case2$教育程度,Case2$观点);T3
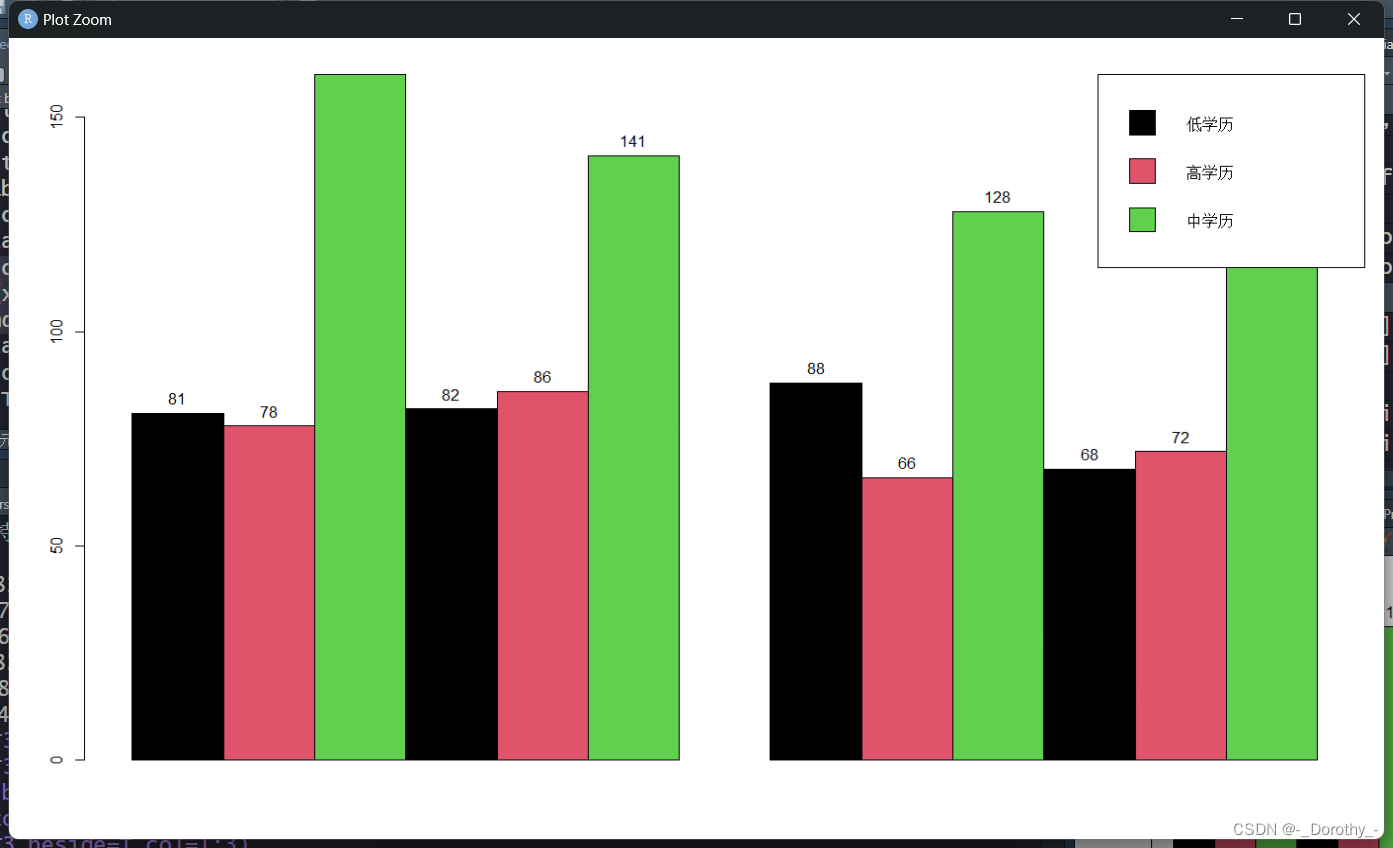
barplot(T3,beside=T,col=1:3)
text(x = barplot(T3, beside = TRUE, col = 1:3), y = T3, labels = T3, pos = 3)
legend("topright", legend = c("低学历", "高学历", "中学历"), fill = 1:3)
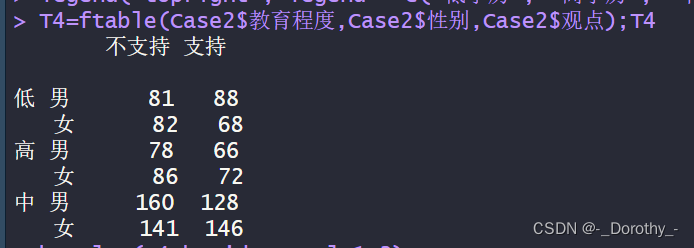
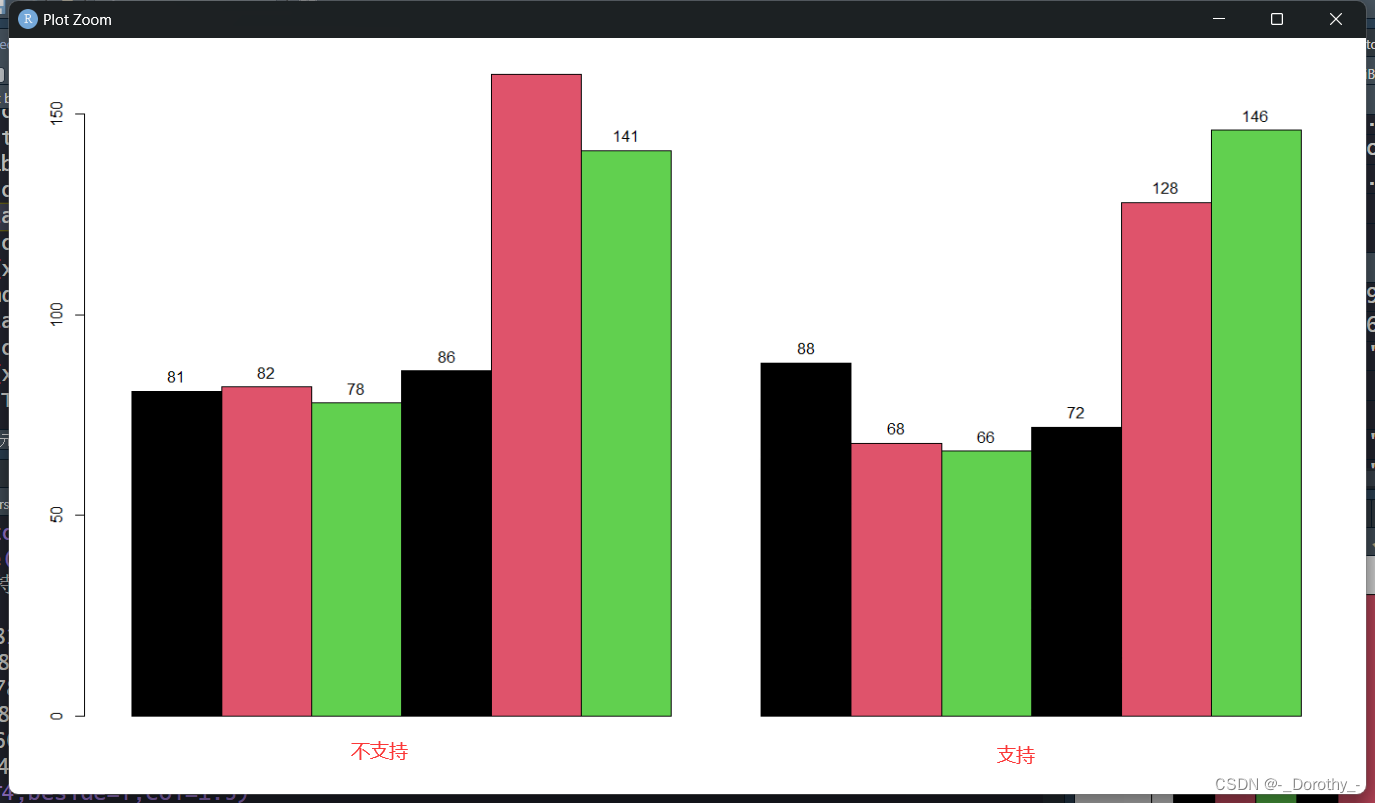
T4=ftable(Case2$教育程度,Case2$性别,Case2$观点);T4
barplot(T4,beside=T,col=1:3)
text(x = barplot(T4, beside = TRUE, col = 1:3), y = T4, labels = T4, pos = 3)
rm(f,T1,T2,T3,T4)#rm全称remove
条形图绘制注意事项
barplot(T2,beside=T,horiz = T,col=1:2)
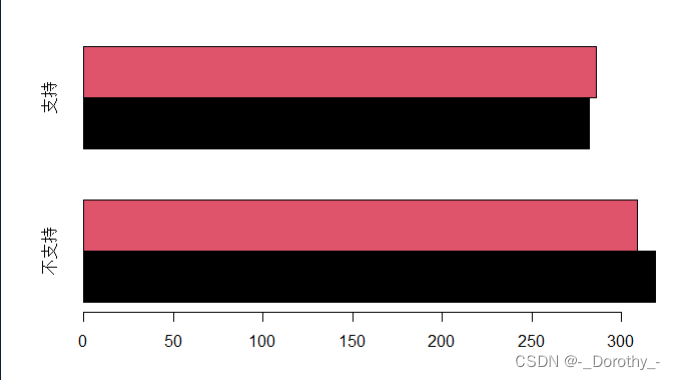
T2:表示要绘制条形图的数据集。
beside=T:表示将多个条形图并排显示,而不是重叠显示。
horiz=T:表示将条形图水平显示,而不是垂直显示。
col=1:2:表示设置条形图的颜色,其中1代表第一种颜色,2代表第二种颜色。
这段代码的作用是将数据集T2的数据以水平并排的方式绘制成条形图,并使用两种不同的颜色进行区分。
barplot()对比
T3()
T3=ftable(Case2$性别,Case2$教育程度,Case2$观点);T3
barplot(T3,beside=T,col=1:3)
text(x = barplot(T3, beside = TRUE, col = 1:3), y = T3, labels = T3, pos = 3)
legend("topright", legend = c("低学历", "高学历", "中学历"), fill = 1:3)
topright代表图例在右上方
T4()
T4=ftable(Case2$教育程度,Case2$性别,Case2$观点);T4
barplot(T4,beside=T,col=1:3)
text(x = barplot(T3, beside = TRUE, col = 1:3), y = T3, labels = T3, pos = 3)