【经典算法】LeetCode112. 路径总和(Java/C/Python3/Go实现含注释说明,Easy)

news2024/11/26 17:45:03

  • 作者主页： 🔗进朱者赤的博客

  • 精选专栏：🔗经典算法

  • 作者简介：阿里非典型程序员一枚 ，记录在大厂的打怪升级之路。 一起学习Java、大数据、数据结构算法（公众号同名）

  • ❤️觉得文章还不错的话欢迎大家点赞👍➕收藏⭐️➕评论，💬支持博主，记得点个大大的关注，持续更新🤞
    ————————————————-

题目描述

给定一个二叉树和一个目标和，判断该树中是否存在从根节点到叶子节点的路径，
这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

示例 1：
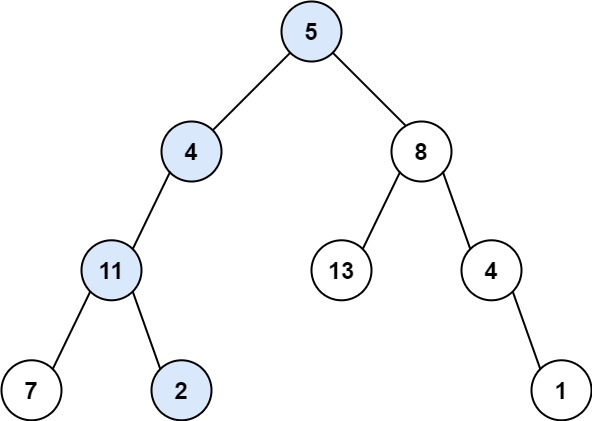
在这里插入图片描述

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。
示例 2：

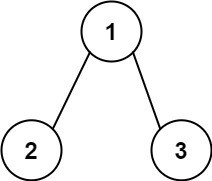
在这里插入图片描述

输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。
示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000
原题：LeetCode 112

思路及实现

方式一：递归深度优先搜索（DFS）

思路

  • 遍历树的每一个节点。
  • 对于每个节点，判断当前节点到根节点的路径和是否等于目标和，如果等于且当前节点是叶子节点，则返回true。
  • 如果不等于，则继续递归遍历左子树和右子树，并更新目标和为当前目标和减去当前节点的值。

代码实现

Java版本
class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}

public class Solution {
    public boolean hasPathSum(TreeNode root, int sum) {
        if (root == null) {
            return false;
        }
        // 如果是叶子节点，且当前路径和等于目标和
        if (root.left == null && root.right == null) {
            return sum == root.val;
        }
        // 递归遍历左子树和右子树
        return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
    }
}

说明：Java版本使用了递归深度优先搜索的方式，遍历树的每个节点，并不断更新目标和值。

C语言版本
#include <stdbool.h>

struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
};

bool hasPathSum(struct TreeNode* root, int sum){
    if (root == NULL) {
        return false;
    }
    if (root->left == NULL && root->right == NULL) {
        return sum == root->val;
    }
    return hasPathSum(root->left, sum - root->val) || hasPathSum(root->right, sum - root->val);
}

说明：C语言版本与Java版本类似，也使用了递归深度优先搜索的方式。

Python3版本
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def hasPathSum(self, root: TreeNode, sum: int) -> bool:
        if not root:
            return False
        if not root.left and not root.right:
            return sum == root.val
        return self.hasPathSum(root.left, sum - root.val) or self.hasPathSum(root.right, sum - root.val)

说明：Python3版本也使用了递归深度优先搜索的方式。

Golang版本
package main

import (
	"fmt"
)

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func hasPathSum(root *TreeNode, sum int) bool {
	if root == nil {
		return false
	}
	if root.Left == nil && root.Right == nil {
		return sum == root.Val
	}
	return hasPathSum(root.Left, sum-root.Val) || hasPathSum(root.Right, sum-root.Val)
}

func main() {
	// 示例代码，实际使用时需要构建二叉树
	// ...
	fmt.Println(hasPathSum(/* root */, /* sum */))
}

说明：Golang版本同样使用了递归深度优先搜索的方式。

复杂度分析

  • 时间复杂度：O(n)，n是二叉树的节点数。每个节点只被访问一次。
  • 空间复杂度：O(h)，h是二叉树的高度。在递归过程中，系统需要为每一层递归调用分配栈空间，因此空间复杂度取决于二叉树的高度。在最坏情况下（树退化为链表），空间复杂度为O(n)。

方式二：迭代深度优先搜索（DFS）

思路

使用栈（Stack）来模拟递归过程，迭代遍历树的每个节点。在遍历过程中，需要额外存储当前路径的路径和（或者称为累积和）。栈中的元素可以是一个自定义的二元组（或结构体），包含当前节点和从根节点到当前节点的路径和。

代码实现

Java版本
import java.util.Stack;

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}

public class Solution {
    public boolean hasPathSum(TreeNode root, int sum) {
        if (root == null) {
            return false;
        }
        
        Stack<TreeNode> nodeStack = new Stack<>();
        Stack<Integer> sumStack = new Stack<>();
        nodeStack.push(root);
        sumStack.push(root.val);
        
        while (!nodeStack.isEmpty()) {
            TreeNode node = nodeStack.pop();
            int currentSum = sumStack.pop();
            
            if (node.left == null && node.right == null) {
                if (currentSum == sum) {
                    return true;
                }
            }
            
            if (node.left != null) {
                nodeStack.push(node.left);
                sumStack.push(currentSum + node.left.val);
            }
            
            if (node.right != null) {
                nodeStack.push(node.right);
                sumStack.push(currentSum + node.right.val);
            }
        }
        
        return false;
    }
}

说明：Java版本使用了两个栈，一个用于存储节点，另一个用于存储从根节点到当前节点的路径和。

C语言版本
#include <stdbool.h>
#include <stdlib.h>

typedef struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
} TreeNode;

typedef struct StackNode {
    TreeNode *node;
    int sum;
    struct StackNode *next;
} StackNode;

typedef struct Stack {
    StackNode *top;
} Stack;

StackNode* createStackNode(TreeNode* node, int sum) {
    StackNode* newNode = (StackNode*)malloc(sizeof(StackNode));
    newNode->node = node;
    newNode->sum = sum;
    newNode->next = NULL;
    return newNode;
}

bool isEmpty(Stack* stack) {
    return stack->top == NULL;
}

void push(Stack* stack, StackNode* node) {
    node->next = stack->top;
    stack->top = node;
}

StackNode* pop(Stack* stack) {
    if (isEmpty(stack)) {
        return NULL;
    }
    StackNode* top = stack->top;
    stack->top = stack->top->next;
    return top;
}

bool hasPathSum(TreeNode* root, int sum) {
    if (root == NULL) {
        return false;
    }
    
    Stack stack;
    stack.top = NULL;
    push(&stack, createStackNode(root, root->val));
    
    while (!isEmpty(&stack)) {
        StackNode* curr = pop(&stack);
        TreeNode* node = curr->node;
        int currentSum = curr->sum;
        free(curr); // Don't forget to free memory allocated for the StackNode
        
        if (node->left == NULL && node->right == NULL) {
            if (currentSum == sum) {
                return true;
            }
        }
        
        if (node->left != NULL) {
            push(&stack, createStackNode(node->left, currentSum + node->left->val));
        }
        
        if (node->right != NULL) {
            push(&stack, createStackNode(node->right, currentSum + node->right->val));
        }
    }
    
    return false;
}

说明：C语言版本使用了自定义的栈结构来模拟递归过程，同时管理节点和路径和。

C++版本

在上面的代码中，我们定义了一个二叉树节点结构TreeNode，并使用std::stack来实现了一个迭代版本的深度优先搜索（DFS）来检查二叉树中是否存在路径和等于给定值的路径。以下是对代码的一些额外说明和注释，以确保理解每个部分的作用。

#include <iostream>
#include <stack>

using namespace std;

// 二叉树节点的定义
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

// 检查是否存在路径和等于给定值的函数
bool hasPathSum(TreeNode* root, int sum) {
    if (root == nullptr) { // 如果根节点为空，则不存在路径
        return false;
    }

    // 使用栈来存储节点和路径和
    stack<pair<TreeNode*, int>> stk; // 栈中每个元素是一个pair，包含节点和到该节点的路径和
    stk.push({root, root->val}); // 初始时将根节点和它的值入栈

    // 当栈不为空时，继续迭代
    while (!stk.empty()) {
        // 弹出栈顶元素
        pair<TreeNode*, int> curr = stk.top();
        stk.pop();

        TreeNode* node = curr.first;
        int currentSum = curr.second;

        // 如果当前节点是叶子节点且路径和等于sum，则返回true
        if (node->left == nullptr && node->right == nullptr && currentSum == sum) {
            return true;
        }

        // 如果左子节点存在，则将其和路径和的增量入栈
        if (node->left != nullptr) {
            stk.push({node->left, currentSum + node->left->val});
        }

        // 如果右子节点存在，则将其和路径和的增量入栈
        if (node->right != nullptr) {
            stk.push({node->right, currentSum + node->right->val});
        }
    }

    // 如果没有找到满足条件的路径，则返回false
    return false;
}

// 测试代码
int main() {
    // 构造一个简单的二叉树进行测试
    // ...（构造二叉树的代码省略）

    int targetSum = 22;
    bool result = hasPathSum(root, targetSum);
    cout << "Does the tree contain a path with sum " << targetSum << "? " << (result ? "Yes" : "No") << endl;

    // 释放二叉树内存（这里只是示例，实际中可能需要递归释放）
    // ...（释放二叉树内存的代码省略）

    return 0;
}

说明
在上面的代码中，我添加了注释来解释每个部分的作用。在hasPathSum函数中，我们使用了一个std::stack来存储节点和路径和的pair。我们首先将根节点和它的值压入栈中，然后进入一个循环，只要栈不为空就继续迭代。在每次迭代中，我们弹出栈顶元素，检查它是否满足路径和等于给定值sum的条件。如果不满足，我们就检查它的左子节点和右子节点是否存在，如果存在，我们就将它们和路径和的增量压入栈中。最后，如果栈为空且没有找到满足条件的路径，我们就返回false。
在main函数中，我们构造了一个二叉树，并调用了hasPathSum函数来检查是否存在路径和等于给定值的路径。然后，我们输出了结果，并注释了释放二叉树内存的部分（这部分在实际应用中需要根据具体的二叉树结构来实现）。

Python3 版本
# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def hasPathSum(root: TreeNode, sum: int) -> bool:
    if not root:  # 如果根节点为空，则不存在路径
        return False
    
    if not root.left and not root.right:  # 如果是叶子节点，检查路径和是否等于sum
        return root.val == sum
    
    # 递归检查左子树和右子树
    left_has_path = hasPathSum(root.left, sum - root.val)
    right_has_path = hasPathSum(root.right, sum - root.val)
    
    # 只要左子树或右子树中存在满足条件的路径，就返回True
    return left_has_path or right_has_path
Golang 版本
package main

import (
	"fmt"
)

// TreeNode represents a binary tree node.
type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

// hasPathSum checks if there's a path in the binary tree with the given sum.
func hasPathSum(root *TreeNode, sum int) bool {
	if root == nil { // 如果根节点为空，则不存在路径
		return false
	}
	
	if root.Left == nil && root.Right == nil { // 如果是叶子节点，检查路径和是否等于sum
		return root.Val == sum
	}
	
	// 递归检查左子树和右子树
	leftHasPath := hasPathSum(root.Left, sum-root.Val)
	rightHasPath := hasPathSum(root.Right, sum-root.Val)
	
	// 只要左子树或右子树中存在满足条件的路径，就返回true
	return leftHasPath || rightHasPath
}

func main() {
	// ... (构造二叉树并调用函数的代码)
	// 例如：
	// root := &TreeNode{Val: 5}
	// root.Left = &TreeNode{Val: 4}
	// root.Right = &TreeNode{Val: 8}
	// ... (继续构造二叉树)
	// sum := 22
	// fmt.Println(hasPathSum(root, sum))
}

说明

复杂度分析

  • 时间复杂度：O(N)，其中N是二叉树的节点数。在最坏情况下，我们需要遍历二叉树中的所有节点。
  • 空间复杂度：O(H)，其中H是二叉树的高度。递归调用栈的深度最多为二叉树的高度。在平均情况下，树是平衡的，其高度为O(logN)，但在最坏情况下（例如，树退化为链表），高度为O(N)。

总结

方式优点缺点时间复杂度空间复杂度
递归深度优先搜索（DFS）1. 代码简洁，逻辑清晰 2. 易于理解和实现1. 对于大型树，可能引发栈溢出 2. 递归调用栈占用额外空间O(N)O(H)，其中H为树的高度，最坏情况下为O(N)
迭代深度优先搜索（DFS）1. 避免了栈溢出问题 2. 空间复杂度相对较低1. 需要使用辅助数据结构（如栈） 2. 代码实现相对复杂O(N)O(N) 或 O(H)，取决于使用的辅助数据结构

相似题目

以下是几个与“检查二叉树中是否存在路径和等于给定值”相似的题目，以及它们的难度和链接：

相似题目难度链接
leetcode 112 路径总和简单力扣-112
leetcode 113 路径总和 II中等力扣-113
leetcode 437 路径总和 III中等力扣-437
leetcode 129 求根到叶子节点数字之和中等力扣-129
leetcode 543 二叉树的直径简单力扣-543

注意：以上链接均指向力扣（LeetCode）中国区的题目页面。如果需要访问国际版，可以将链接中的 “leetcode-cn.com” 替换为 “leetcode.com”。

欢迎一键三连(关注+点赞+收藏)，技术的路上一起加油！！！代码改变世界

  • 关于我：阿里非典型程序员一枚 ，记录在大厂的打怪升级之路。 一起学习Java、大数据、数据结构算法（公众号同名），回复暗号，更能获取学习秘籍和书籍等

  • —⬇️欢迎关注下面的公众号：进朱者赤，认识不一样的技术人。⬇️—

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1639319.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Agent AI智能体：如何借助机器学习引领科技新潮流

Agent AI智能体：如何借助机器学习引领科技新潮流

文章目录 &#x1f4d1;前言一、Agent AI智能体的基本概念二、Agent AI智能体的技术进步2.1 机器学习技术2.2 自适应技术2.3 分布式计算与云计算 三、Agent AI智能体的知识积累3.1 知识图谱3.2 迁移学习 四、Agent AI智能体的挑战与机遇4.1 挑战4.2 机遇 小结 &#x1f4d1;前言…
阅读更多...
004 秒杀下单

004 秒杀下单

文章目录 超卖问题方案一方案二方案三aop锁(单机锁)aop锁(单机锁)pom.xmlLockAspect.javaServiceLock.java 分布式锁Mysql分布式锁Redis分布式锁ServiceRedisLock.javaLockRedisAspect.java 下单性能优化数据一致性解决一致性问题异步同步库存 秒杀下单业务步骤: 1.数据校验(身…
阅读更多...
DS：顺序表、单链表的相关OJ题训练

DS：顺序表、单链表的相关OJ题训练

欢迎各位来到 Harper.Lee 的学习小世界&#xff01; 博主主页传送门&#xff1a;Harper.Lee的博客主页 想要一起进步的uu可以来后台找我交流哦&#xff01; 在DS&#xff1a;单链表的实现 和 DS&#xff1a;顺序表的实现这两篇文章中&#xff0c;我详细介绍了顺序表和单链表的…
阅读更多...
Unity SteamVR入门

Unity SteamVR入门

概述 VR项目现在在当前已经是非常热门的技术&#xff0c;可以给玩家身临其境的感觉&#xff0c;接下来让我们学习这部分的内容吧&#xff01; SteamVR Input SteamVR绑定流程&#xff0c;在Windows窗口的点击SteamVR-input&#xff0c;图1&#xff0c;在这里可以选择你需要绑定…
阅读更多...
Photoshop前言

Photoshop前言

Photoshop前言 分辨率图像格式工具界面组件 分辨率 分辨率是指单位长度内包含的像素点的数量&#xff0c;其单位通常为像素/英寸&#xff08;ppi&#xff09;&#xff0c;300ppi表示每英寸包含300个像素点。对于1英寸1英寸大小的图像&#xff0c;若分辨率为72ppi&#xff0c;则…
阅读更多...
Unity MeshRenderer 入门

Unity MeshRenderer 入门

概述 在项目制作过程中&#xff0c;肯定缺少不了模型的使用&#xff0c;那就一定接触过MeshRenderer&#xff0c;也许还有你不理解的地方&#xff0c;接下来让我们来学习一下这部分的内容吧。 Mesh Filter&#xff08;网格过滤器&#xff09; Mesh:提供一个网格的参考&#xf…
阅读更多...
# notepad++ 编辑器英文版，如何打开自动换行

# notepad++ 编辑器英文版，如何打开自动换行

notepad 编辑器英文版&#xff0c;如何打开自动换行 在Notepad中&#xff0c;如果你想要开启自动换行功能&#xff0c;可以按照以下步骤操作&#xff1a; 1、打开 Notepad 编辑器。 1.1. 依次点击菜单栏中的【视图】&#xff0c;英文版对应【View】。1.2. 在【视图】下拉菜单…
阅读更多...
Integer中的缓存机制

Integer中的缓存机制

先看一个示例&#xff1a; public static void main(String[] args) {Integer a127;Integer b127;System.out.println(ab);Integer c128;Integer d128;System.out.println(cd);} 输出&#xff1a; true false 为什么明明都是同一个数字进行比较&#xff0c;当数字等于127的…
阅读更多...
串口单线半双工转换电路

串口单线半双工转换电路

用来把单线半双工模式的串口转换成双线&#xff0c;然后才能连接到普通的双线USB 串口模块&#xff0c;比如CH340 之类的。电路设计来自大佬的博客&#xff1a;AVR half-duplex software UART supporting single pin operation。他在Arduino 上用软件模拟串口功能&#xff0c;利…
阅读更多...
【火猫DOTA2】电竞世界杯DOTA2项目将在7月份的前三周举办

【火猫DOTA2】电竞世界杯DOTA2项目将在7月份的前三周举办

1、电竞世界杯将于今年7月3日至8月25日在沙特利雅得举办。近日主办方公布了各个项目的举办时间,其中DOTA2项目将在7月份的前三周举办。转载:火猫TV资讯https://www.huomaotv.com/ 目前Falcons、XG、GG和Liquid这五支赢得了足够EPT积分的队伍已经确定直邀沙特。剩下的三个名额还…
阅读更多...
nginx的前世今生（二）

nginx的前世今生（二）

书接上回&#xff1a; 上回书说到&#xff0c;nginx的前世今生&#xff0c;这回我们继续说 3.缓冲秘籍&#xff0c;洪流控水 Nginx的缓冲区是其处理数据传输和提高性能的关键设计之一&#xff0c;主要用于暂存和管理进出的数据流&#xff0c;以应对不同组件间速度不匹配的问题…
阅读更多...
图片高效批量美化，支持将图片进行旋转180度并生成浴室玻璃图片，让图片瞬间焕然一新！

图片高效批量美化，支持将图片进行旋转180度并生成浴室玻璃图片，让图片瞬间焕然一新！

图片已成为我们生活与工作中不可或缺的一部分。然而&#xff0c;一张张手动美化图片却是一项既耗时又耗力的任务。为了帮助您轻松应对这一挑战&#xff0c;我们推出了一款高效批量美化图片的工具&#xff0c;并支持将图片旋转180度及生成浴室玻璃效果&#xff0c;让您的图片瞬间…
阅读更多...
安装英伟达nvidia p4计算卡驱动@FreeBSD14

安装英伟达nvidia p4计算卡驱动@FreeBSD14

FreeBSD也能跑cuda AI训练拉&#xff01; 在FreeBSD安装好pytorch和飞桨cpu版本后&#xff0c;尝试安装英伟达nvidia p4计算卡驱动。毕竟全靠cpu速度太慢了&#xff0c;还是GPU快啊&#xff01;在磕磕绊绊几天后&#xff0c;终于成功成功安装好nvidia p4的cuda驱动&#xff0c…
阅读更多...
拆单算法交易（Algorithmic Trading）

拆单算法交易（Algorithmic Trading）

TWAP TWAP交易时间加权平均价格Time Weighted Average Price 模型&#xff0c;是把一个母单的数量平均地分配到一个交易时段上。该模型将交易时间进行均匀分割&#xff0c;并在每个分割节点上将拆分的订单进行提交。例如&#xff0c;可以将某个交易日的交易时间平均分为N 段&am…
阅读更多...
密码学基础练习五道 RSA、elgamal、elgamal数字签名、DSA数字签名、有限域(GF)上的四则运算

密码学基础练习五道 RSA、elgamal、elgamal数字签名、DSA数字签名、有限域(GF)上的四则运算

1.RSA #include <stdlib.h>#include <stdio.h>#include <string.h>#include <math.h>#include <time.h>#define PRIME_MAX 200 //生成素数范围#define EXPONENT_MAX 200 //生成指数e范围#define Element_Max 127 //加密单元的…
阅读更多...
26版SPSS操作教程（高级教程第十八章）

26版SPSS操作教程（高级教程第十八章）

目录 前言 粉丝及官方意见说明 第十八章一些学习笔记 第十八章一些操作方法 经典判别分析 数据假设 具体操作 结果解释 判别结果的图形化展示 结果解释 判别效果验证 结果解释 适用条件的判断 结果解释 贝叶斯判别分析 具体操作 结果解释 逐步判别法 结束语…
阅读更多...
Redis---------实现查询缓存业务

Redis---------实现查询缓存业务

目录 数据库与缓存之间的工作业务逻辑&#xff1a; 接下来看查询缓存代码实现&#xff0c;主要是捋清楚业务逻辑&#xff0c;代码实现是死的&#xff1a; Controller: Service: P37作业实现&#xff1a;总体逻辑跟上面的业务逻辑差不多 Controller&#xff1a; Service&#…
阅读更多...
【项目构建】04：动态库与静态库制作

【项目构建】04：动态库与静态库制作

OVERVIEW 1.编译动态链接库&#xff08;1&#xff09;编译动态库&#xff08;2&#xff09;链接动态库&#xff08;3&#xff09;运行时使用动态库 2.编译静态链接库&#xff08;1&#xff09;编译静态库&#xff08;2&#xff09;链接静态库&#xff08;3&#xff09;运行时使…
阅读更多...
数字身份管理：Facebook如何利用区块链技术？

数字身份管理：Facebook如何利用区块链技术？

随着数字化进程的加速&#xff0c;个人身份管理已成为一个关键议题。在这方面&#xff0c;区块链技术正在逐渐展现其巨大潜力。作为全球最大的社交媒体平台&#xff0c;Facebook也在积极探索和应用区块链技术来改进其数字身份管理系统。本文将深入探讨Facebook如何利用区块链技…
阅读更多...
【Docker学习】docker start深入研究

【Docker学习】docker start深入研究

docker start也是很简单的命令。但因为有了几个选项&#xff0c;又变得复杂&#xff0c;而且... 命令&#xff1a; docker container start 描述&#xff1a; 启动一个或多个已停止的容器。 用法&#xff1a; docker container start [OPTIONS] CONTAINER [CONTAINER...] 别名&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023