线性与非线性模型及R使用
文章目录
- 线性与非线性模型及R使用
- 一、数据的分类与模型选择
- 1.变量的取值类型
- 二、广义线性模型
- 广义线性模型概述
- Logistic模型
- 总结
一、数据的分类与模型选择
1.变量的取值类型
因变量记为y,解释变量记为x1,x2,…
因变量y一般有如下五种取值方式:
(1)y为连续变量,如心脏面积、肺活量、血红蛋白量等。
(2)y为“0-1”变量或称二分类变量,如实验“成功”、“失败”,“有效”、“无效”,治疗结果“存活”、“死亡”等。
(3)y为有序变量(等级变量),如治疗结果“治愈”、“显效”、“无效”等。
(4)y为多分类变量,如脑肿瘤分良性、恶性、转移瘤,小儿肺炎分结核性、化脓性和细菌性等。
(5)y为连续伴有删失变量,如某病治疗后存活时间可能有失访删失、终检删失和随机删失等。
解释变量x一般有如下三种取值方式:
(1)x为连续变量,如身高、体重等,一般称x为自变量或协变量。
(2)x为分类变量,如性别:男、女,居住地:城市、村镇、农村等,称x为因素。
(3)x为等级变量,如吸烟量:不吸烟、0–10支、10~20支、20支以上等,x可通过评分转化为协变量,也可以看成因素,等级数看成是因素的水平数。
二、广义线性模型
广义线性模型概述
因变量为非正态分布线性模型称为广义线性模型
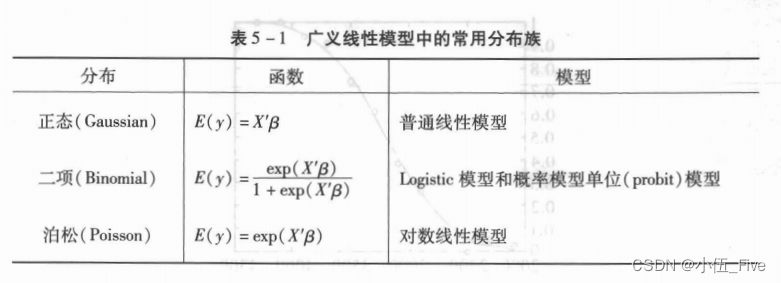
在R语言中,正态(高斯)分布族的广义线性模型事实上同线性模型是相同的,即
gm <-glm(formula,family=gaussian,data)
同线性模型
fm <-Im(formula,data)
得到的结论是一致的,当然,其效率会差很多。

Logistic模型
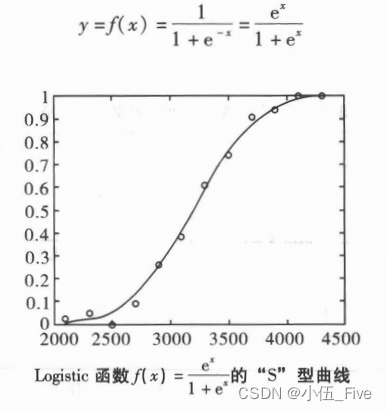
实例分析:
对45名驾驶员的调查结果
> nk=read.table("clipboard",header=T)
> logit.glm<-glm(y~x1+x2+x3,family=binomial,data=nk)
> summary(logit.glm)#Logistic回归模型结果
Call:
glm(formula = y ~ x1 + x2 + x3, family = binomial, data = nk)
Coefficients
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.597610 0.894831 0.668 0.5042
x1 -1.496084 0.704861 -2.123 0.0338 *
x2 -0.001595 0.016758 -0.095 0.9242
x3 0.315865 0.701093 0.451 0.6523
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 62.183 on 44 degrees of freedom
Residual deviance: 57.026 on 41 degrees of freedom
AIC: 65.026
Number of Fisher Scoring iterations: 4

> logit.step<-step(logit.glm,direction="both")#逐步筛选法变量选择
Start: AIC=65.03
y ~ x1 + x2 + x3
Df Deviance AIC
- x2 1 57.035 63.035
- x3 1 57.232 63.232
<none> 57.026 65.026
- x1 1 61.936 67.936
Step: AIC=63.03
y ~ x1 + x3
Df Deviance AIC
- x3 1 57.241 61.241
<none> 57.035 63.035
+ x2 1 57.026 65.026
- x1 1 61.991 65.991
Step: AIC=61.24
y ~ x1
Df Deviance AIC
<none> 57.241 61.241
+ x3 1 57.035 63.035
+ x2 1 57.232 63.232
- x1 1 62.183 64.183
> summary(logit.step)#逐步筛选法变量选择结果
Call:
glm(formula = y ~ x1, family = binomial, data = nk)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.6190 0.4688 1.320 0.1867
x1 -1.3728 0.6353 -2.161 0.0307 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 62.183 on 44 degrees of freedom
Residual deviance: 57.241 on 43 degrees of freedom
AIC: 61.241
Number of Fisher Scoring iterations: 4

> pre1<-predict(logit.step,data.frame(x1=1))#预测视力正常司机Logistic回归结果
> p2<-exp(pre2)/(1+exp(pre2))#预测视力有问题的司机发生事故概率
错误: 找不到对象'pre2'
> p1<-exp(pre1)/(1+exp(pre1))#预测视力正常司机发生事故概率
> pre2<-predict(logit.step,data.frame(x1=0))#预测视力有问题的司机Logistic回归结果
> p2<-exp(pre2)/(1+exp(pre2))#预测视力有问题的司机发生事故概率
> c(p1,p2)#结果显示
1 1
0.32 0.65
可见,P1=0.32,P2=0.65,说明视力有问题的司机发生交通事故的概率是视力正常的司机的两倍以上。
总结
本小节主要学习了数据的分类与模型选择以及广义线性模型,尤其是 Logistic模型的方法介绍和实际应用操作,继续加油!