c语言——二叉树

news2024/11/23 15:46:55

目录

目录

二叉树关键概念理解

一颗拥有1000个结点的树度为4，则它的最小深度是？

那么对于二叉树，只掌握这些是远远不够的，我们还需要掌握几个最基本的经典问题，

求二叉树大小

求叶子结点个数 

求深度

求第k层的结点个数

寻找值为k的结点

遍历打印

判断二叉树是否是完全二叉树

销毁

二叉树的构建 

 1.    求二叉树大小

 2.    求叶子结点个数 

3.求深度

需要注意的是：需要每次存储每次递归的大小， 优化时间

4.求第k层的结点个数

5.寻找值为k的结点

 需要注注意的是需要存储每次递归的ret，优化时间

6.层序遍历打印

前序： 根->左子树->右子树

中序： 左子树->根->右子树

后序： 左子树->右子树->根

层序 ：一层一层打印

7. 判断二叉树是否是完全二叉树

8.销毁

一颗拥有1000个结点的树度为4，则它的最小深度是？

那么对于二叉树，只掌握这些是远远不够的，我们还需要掌握几个最基本的经典问题，

求二叉树大小

求叶子结点个数 

求深度

求第k层的结点个数

寻找值为k的结点

遍历打印

判断二叉树是否是完全二叉树

销毁

二叉树的构建 

 1.    求二叉树大小

 2.    求叶子结点个数 

3.求深度

需要注意的是：需要每次存储每次递归的大小， 优化时间

4.求第k层的结点个数

5.寻找值为k的结点

 需要注注意的是需要存储每次递归的ret，优化时间

6.层序遍历打印

前序： 根->左子树->右子树

中序： 左子树->根->右子树

后序： 左子树->右子树->根

层序 ：一层一层打印

7. 判断二叉树是否是完全二叉树

8.销毁

二叉树关键概念理解

二叉树的概念在这里就不进行过多的赘述，那么主要说一下我认为重要的部分，

第一点就是二叉树里面部分概念的理解：

就比如说，你对于如何构建二叉树，掌握的十分深刻，但刷题的时候对于一些题目所给的概念不清楚，导致看不明白题目，这课不好，

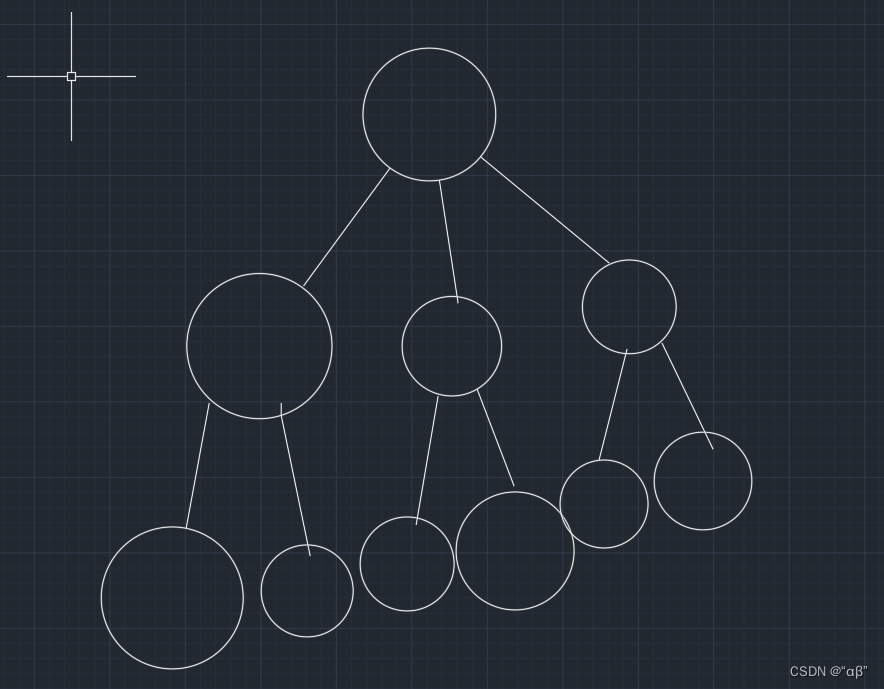
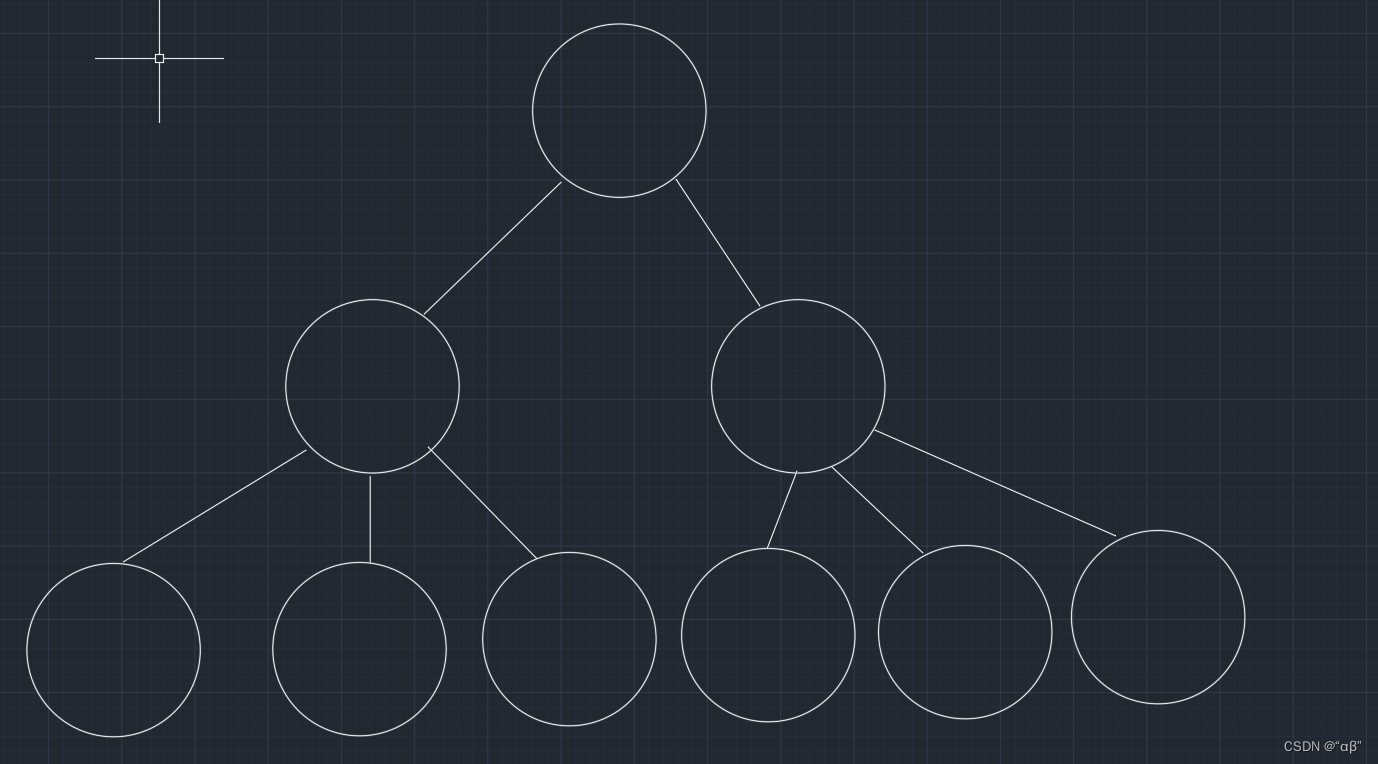
二叉树的概念如下图所示,其实都很简单，主要是当给他的名字时，你明不明白。

还有对于满二叉树与完全二叉树 需要注意的就是完全二叉树，最后一层，从左到右时必须连续的。 

 经过看过这两张图后，再加上我们原本的二叉树基础，我们看几道题：

一颗拥有1000个结点的树度为4，则它的最小深度是？

 如果我们了解度的概念，那么就很好计算出答案。

那么思路：最小度数就是当每个结点都是满的情况下，那么就为最小深度，

设高度为h，那么每个结点都是满的情况下，通过数学计算得出，此时总共结点数：（4^h-1)/3,那么h=5时，最大结点数为341，h=6时，为1365，

那么最小深度就为6.

 2-3树是一种特殊的树，它满足两个条件：

(1) 每个内部结点有两个或三个子结点

(2) 所有的叶结点到根的距离相同

如果一颗2-3树有10个结点，那么它有( )个叶结点

对于本道题，经过分析，我们得知，第二层一定是只有两个结点,或三个结点，

当为三个结点时，只有这一种情况：

 当为二个结点时：

再最多的情况下也只可以放九个

所以就只有6个叶子结点。

那么对于二叉树，只掌握这些是远远不够的，我们还需要掌握几个最基本的经典问题，

  1. 求二叉树大小

  2. 求叶子结点个数 

  3. 求深度

  4. 求第k层的结点个数

  5. 寻找值为k的结点

  6. 遍历打印

  7. 判断二叉树是否是完全二叉树

  8. 销毁

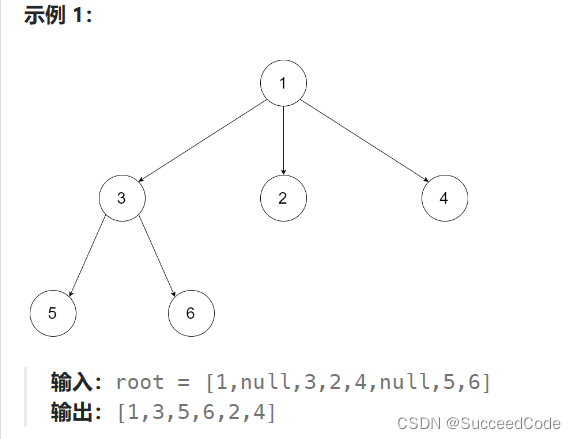
二叉树的构建 

//二叉树
typedef int BTDataType;
typedef struct BTNode
{
	BTDataType val;
	struct BTNode* left;
	struct BTNode* right;
}BTNode;
BTNode* Creat_Node()
{
	BTNode* Node1 = BuyNode(1);
	BTNode* Node2 = BuyNode(2);
	BTNode* Node3 = BuyNode(3);
	BTNode* Node4 = BuyNode(4);
	BTNode* Node5 = BuyNode(5);
	BTNode* Node6 = BuyNode(6);
	//BTNode* Node7 = BuyNode(7);
	Node1->left = Node2;
	Node1->right = Node4;
	Node2->left = Node3;
	Node4->left = Node5;
	Node4->right = Node6;
	//Node6->right = Node7;
	return Node1;
}

BTNode* BuyNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
	}
	node->val = x;
	node->left = NULL;
	node->right = NULL;
	return node;
}

 接下来依次介绍

 1.    求二叉树大小

代码实现：

int BT_Size(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return BT_Size(root->left) + BT_Size(root->right) + 1;
}

或者： 

int BT_Size(BTNode* root)
{
	return root == NULL ? 0 : BT_Size(root->left) +
		BT_Size(root->right) + 1;
}

 2.    求叶子结点个数 

 叶子结点有一个特点，那么就是左节点与右节点全为空，只要抓住这一点特点，利于递归，还是很好实现的。

int BT_Leaf_Size(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return BT_Leaf_Size(root->left) +
		BT_Leaf_Size(root->right);
}

3.求深度

求二叉树深度可以转化为求左子树的深度，与右子树的深度，然后比比谁的大，然后左子树深度求法又可以分为，求左子树的左子树与右子树的深度，以此类推。

需要注意的是：需要每次存储每次递归的大小， 优化时间

int BT_Depth_Size(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int left_Depth_Size = BT_Depth_Size(root->left);
	int right_Depth_Size = BT_Depth_Size(root->right);
	return left_Depth_Size > right_Depth_Size ?
		BT_Depth_Size(root->left) + 1 : 
		BT_Depth_Size(root->right) + 1;
}

4.求第k层的结点个数

 思路就是首先我们要先找到第k层所在位置，然后每找到一个就利用递归然会去1；

int BT_Size_Levre_k(BTNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return BT_Size_Levre_k(root -> left, k - 1) +
		BT_Size_Levre_k(root -> right, k - 1);
}

5.寻找值为k的结点

 需要注注意的是需要存储每次递归的ret，优化时间

BTNode* BTFind_Data_k(BTNode* root, int k)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->val == k)
	{
		return root;
	}
	BTNode* ret1 = BTFind_Data_k(root->left, k);
	if (ret1)
	{
		return ret1;
	}
	BTNode* ret2 = BTFind_Data_k(root->right, k);
	if (ret2)
	{
		return ret2;
	}
	return NULL;
}

6.层序遍历打印

前序： 根->左子树->右子树

void Prev_Order(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	printf("%d ", root->val);
	Prev_Order(root->left);
	Prev_Order(root->right);
}

中序： 左子树->根->右子树

void In_Order(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	In_Order(root->left);
	printf("%d ", root->val);
	Prev_Order(root->right);
}

后序： 左子树->右子树->根

void Post_Order(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	In_Order(root->left);
	Prev_Order(root->right);
	printf("%d ", root->val);
}

层序 ：一层一层打印

层序打印需要运用到栈，这里不提供栈的实现了，只提供实现层序打印的代码

void Lever_Order(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ", front->val);
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	printf("\n");
}

7. 判断二叉树是否是完全二叉树

 检查是否为完全二叉树，也是利用栈的知识来实现，因为在层序遍历的时候，是出完一层的时候也会在进完下一层，并且顺序是完全按照一层一层从左到右

所以实现思路就为，先找到第一个为空的结点，然后查看他后面的结点是不是为空，如果为空，那么就为完全二叉树，反之不是。

bool BinaryTreeComplete(BTNode* root)
{
	//层序遍历，从第一个为空开始，向后看是否为空
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front == NULL)
		{
			break;
		}
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
	}
	//检查后面是否为空  ，有非空即不是完全二叉树
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)
		{
			return false;
		}
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	return true;
}

8.销毁

void BinaryTreeDestory(BTNode* root)//后序顺序释放
{
	if (root == NULL)
	{
		return;
	}
	BinaryTreeDestory(root->left);
	BinaryTreeDestory(root->right);
	free(root);
}

还有一些结论：

1：二叉树第i层上的结点数目最多为2i-1(i>=1)

2：深度为k的二叉树至多有2^(k) - 1个结点（k>=1）,叶子节点为 2^(k - 1) 

3：包含n个结点的二叉树的高度至少为( log2(n) )+1

4：在任意一棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则n0=n2+1

5：leftchild=parent*2+1;   rightchild=parent*2+2;

6:  parent=(child-1)/2;

7: 令度为0，的结点个数为N0,度为2的个数为N2

那么N0=N2+1；

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1639120.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

如何快速的追加文章的内容（在不知道内容的情况下）

如何快速的追加文章的内容（在不知道内容的情况下）

首先，需要用到的这个工具： 度娘网盘 提取码：qwu2 蓝奏云 提取码：2r1z 1、打开工具，切换到文章模块下，快捷键：Ctrl1 2、新建一个文章做演示，001 3、添加一个内容，就随…
阅读更多...
【IO操作】标准IO和文件IO

【IO操作】标准IO和文件IO

一.标准IO和文件IO的区别 （1）一般标准IO指的是C语言的IO操作，文件IO一般指的是Linux系统调用的IO操作。标准O因为是C语言提供的标准库，所以可以在其他操作系统平台编译后可以执行，但是文件IO只能在Linux下使用&#x…
阅读更多...
C语言高效学习、提升方法

C语言高效学习、提升方法

前言 已经用了十多年的C语言，回头看怎么学习、提升最快呢？个人觉得还是要从框架上去着手学习，用全局眼光去看、去学，主要是三部分：关键字及基本语法、重点功能点及标准库函数；只要把这三部分基本搞懂了&am…
阅读更多...
AD | Altium Designer(原理图设计、电路仿真、PCB绘图)汉化版

AD | Altium Designer(原理图设计、电路仿真、PCB绘图)汉化版

Altium Designer(原理图设计、电路仿真、PCB绘图) 通知公告 Altium Designer（AD）是一种功能强大的电子设计自动化（EDA）软件。它主要用于设计和开发电子产品，如电路板（PCB）、集成电路（IC）和嵌入式系统。AD提供了完整的设计工具套件，包括原理图设计、PCB布局、仿真、设…
阅读更多...
蓝桥杯单片机省赛——第八届“基于单片机的电子钟程序设计与调试”程序部分

蓝桥杯单片机省赛——第八届“基于单片机的电子钟程序设计与调试”程序部分

往期回顾 第三届蓝桥杯单片机省赛 第四届蓝桥杯单片机省赛 第五届蓝桥杯单片机省赛 第六届蓝桥杯单片机省赛 第七届蓝桥杯单片机省赛 文章目录 往期回顾一、前期准备二、代码详情1.基础代码蜂鸣器/继电器/led/定时器之类的代码 2.按键详解按键写法讲解 3.驱动的处理驱动写法讲…
阅读更多...
【前端篇】微信小程序ActionSheet封装 -- 封装特性，开发只需要关注功能

【前端篇】微信小程序ActionSheet封装 -- 封装特性，开发只需要关注功能

大家好啊，这次来分享一下小程序开发的一个使用封装。 背景 先来看下什么是ActionSheet，参考下图（来源：豆流便签） 参考原生代码实现： wx.showActionSheet({itemList: ["action1", "actio…
阅读更多...
万万没想到，延缓帕金森病进展的“玄机”竟然就在腿上？【北京仁爱堂】

万万没想到，延缓帕金森病进展的“玄机”竟然就在腿上？【北京仁爱堂】

帕金森病患者的腿部变化，其实可以反应出很多问题。例如行走的变化问题、步态的异常等问题，可以反应病情轻重程度。而通过保持腿部肌肉活动的状态，也可以使帕金森病的症状得到一定的缓解，甚至有助于防止病情恶化。 帕金森病腿部变…
阅读更多...
C++类和对象上篇

C++类和对象上篇

🐇 🔥博客主页： 云曦 📋系列专栏：[C] 💨路漫漫其修远兮 吾将而求索 💛 感谢大家👍点赞 😋关注📝评论 文章目录 📙前言📙1、面向过程…
阅读更多...
Java创建并遍历N叉树（前序遍历）

Java创建并遍历N叉树（前序遍历）

力扣 title589：N叉树的前序遍历 给定一个 n 叉树的根节点 root ，返回 其节点值的 前序遍历 。 n 叉树 在输入中按层序遍历进行序列化表示，每组子节点由空值 null 分隔（请参见示例）。 思路： 1.初始化时…
阅读更多...
C++_set和map的学习

C++_set和map的学习

1. 关联式容器 STL中的容器有序列式容器和关联式容器。 其中 vector 、 list 、 deque 、 forward_list(C11)就是序列式容器， 因为其底层为线性序列的数据结构，里面 存储的是元素本身 关联式容器 也是用来存储数据的，与序列式容器不同的是&am…
阅读更多...
企业办公网络安全为何每个企业都要重视

企业办公网络安全为何每个企业都要重视

随着互联网的持续发展，当前大量企业通过网络将集团总部与各分公司/厂区结合起来，便捷的沟通和共享方式大大提高了企业的生产力和工作效率，如何能够保障一个稳定、安全、便捷的整体网络成为企业IT建设的重要课题。对大量企业用户进行调研后发现…
阅读更多...
万界星空科技商业开源MES+项目合作+商业开源低代码平台

万界星空科技商业开源MES+项目合作+商业开源低代码平台

今天我想和大家分享的是一套商业开源的 MES制造执行管理系统带源码。对于制造业而言，MES 是一个至关重要的系统，它可以帮助企业提高生产效率、优化资源利用、提高产品质量，从而增强市场竞争力。 什么是 MES？ MES 是指通过计算机技…
阅读更多...
llama-factory/peft微调千问1.5-7b-chat

llama-factory/peft微调千问1.5-7b-chat

目标 使用COIG-CQIA数据集和通用sft数据集对qwen1.5-7b-chat进行sft微调，使用公开dpo数据集进行dpo对齐。学习千问的长度外推方法。 一、训练配置 使用Lora方式, 将lora改为full即可使用全量微调。 具体的参数在 该框架将各个参数、训练配置都封装好了，直接使用脚本，将数…
阅读更多...
unity项目《样板间展示》开发：菜单界面

unity项目《样板间展示》开发：菜单界面

unity项目《样板间展示》开发：菜单界面 前言UI菜单创建逻辑实现结语 前言 这是这个项目demo教程的最后一节，这节是菜单界面部分的创建 UI菜单创建 创建一个新的场景，在Scene文件中右键选择Create->Scene，创建新的场景 在场景…
阅读更多...
【Linux】创建/扩容swap交换空间swap优化

【Linux】创建/扩容swap交换空间swap优化

一、当前交换空间大小 目前交换空间大小为2G 二、创建swap交换空间 #创建大小为2G的交换空间 [roothadoop01 data1]# dd if/dev/zero of/data1/swapfile bs1M count2048 #将文件设置为交换空间 [roothadoop01 data1]# mkswap /data1/swapfile #启用交换空间 [roothadoop01 da…
阅读更多...
ElasticSearch教程入门到精通——第一部分（基于ELK技术栈elasticsearch 8.x新特性）

ElasticSearch教程入门到精通——第一部分（基于ELK技术栈elasticsearch 8.x新特性）

ElasticSearch教程入门到精通——第一部分（基于ELK技术栈elasticsearch 8.x新特性） 1. ElasticSearch安装（略）2. ElasticSearch基础功能2.1 索引操作2.1.1 创建索引2.1.2 Head 索引2.1.3 查询索引2.1.3.1 查询单独索引2.1.3.2 查询…
阅读更多...
智能产品信息模型-控制信息模型

智能产品信息模型-控制信息模型

数字化的核心是数字化建模，为一个事物构建数字模型是一项十分复杂的工作。不同的应用场景，对事物的关注重点的不同的。例如，对于一个智能传感器而言，从商业的角度看，产品的信息模型中应该包括产品的类型，名…
阅读更多...
Vue 组件的三大组成部分

Vue 组件的三大组成部分

Vue 组件通常由三大组成部分构成：模板（Template）、脚本（Script）、样式（Style） 模板部分是组件的 HTML 结构，它定义了组件的外观和布局。Vue 使用基于 HTML 的模板语法来声明组件的模…
阅读更多...
如何维持CISSP证书：附免费获取CPE学分的16个官方渠道

如何维持CISSP证书：附免费获取CPE学分的16个官方渠道

CISSP 证书只有三年有效期（如2023.11-2026.10），需要每年维护才能续证。持证者需要持续获取 CPE 学分来维持证书，否则证书到期后将失效。本文主要介绍维护CISSP证书的2个必备条件及16个CPE学分官方获取渠道。 1. 证书维持的2个必备…
阅读更多...
AI大模型探索之路-训练篇10：大语言模型Transformer库-Tokenizer组件实践

AI大模型探索之路-训练篇10：大语言模型Transformer库-Tokenizer组件实践

系列篇章💥 AI大模型探索之路-训练篇1：大语言模型微调基础认知 AI大模型探索之路-训练篇2：大语言模型预训练基础认知 AI大模型探索之路-训练篇3：大语言模型全景解读 AI大模型探索之路-训练篇4：大语言模型训练数据集概…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023