多元相关与回归分析及R使用
文章目录
- 多元相关与回归分析及R使用
- 一.变量间的关系分析
- 1.两变量线性相关系数的计算
- 2.相关系数的假设检验
- 二.一元线性回归分析的R计算
- 三、回归系数的假设检验
- 总结
一.变量间的关系分析
变量间的关系及分析方法如下:

1.两变量线性相关系数的计算
两个变量之间的线性相关,用相关系数来表示线性关系,总体相关系数计算公式为:
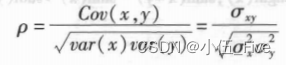

实际中,我们通常计算Pearson相关系数

例:身高与体重的相关关系分析
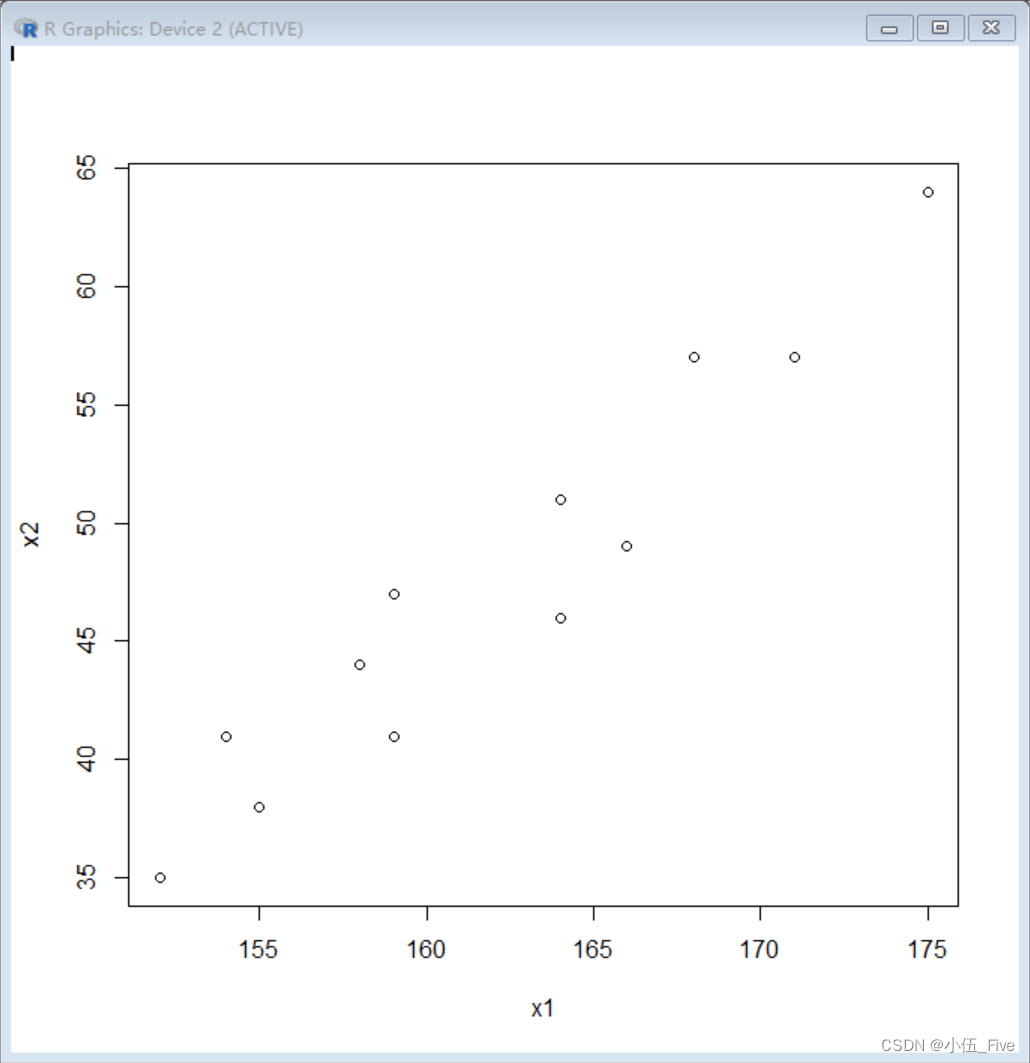
> x1=c(171,175,159,155,152,158,154,164,168,166,159,164) #身高
> x2=c(57,64,41,38,35,44,41,51,57,49,47,46) #体重
> plot(x1,x2)
离均差积和函数
> lxy <- function(x1, x2) {
+ n <- length(x1)
+ sum(x1 * x2) - sum(x1) * sum(x2) / n
+ }
> lxy(x1,x1)
[1] 556.9167
> lxy(x1,x2)
[1] 645.5
> lxy(x2,x2)
[1] 813
> (r=lxy(x1,x2)/sqrt(lxy(x1,x1)*lxy(x2,x2)))
[1] 0.9593031
这里r为正值,说明该组人群的身高与体重之间呈现正的线性相关关系。
当然,R语言中也自带求相关系数的函数
cor(x,y=NULL,method=c(“pearson”,“kendall”,“spearman”))
x为数值向量、矩阵或数据框
y为空或数值向量、矩阵或数据框
method为计算方法,包括"pearson"、"kendall"和"spearman’“三种,默认"pearson”
> cor(x1,x2)
[1] 0.9593031
2.相关系数的假设检验
r与其他统计指标一样,也有抽样误差。从同一总体内抽取若干大小相同的样本,各样本的相关系数总有波动。要判断不等于0的?值是来自总体相关系数ρ=0的总体还是来自P≠0的总体,必须进行显著性检验。
由于来自p=0的总体的所有样本相关系数呈对称分布,故r的显著性可用t检验来进行。

> n=length(x1)
> t=r/sqrt((1-r^2)/(n-2))
> t
[1] 10.74298
计算t值和P值,作结论。
cor.test(x,y,alternative=c(“two.sided”,“less”,“greater”),
method=c(“pearson”,“kendall”,“spearman”),…)
x,y为数据向量(长度相同)
alternative为备择假设,“two.sided”(双侧),“greater”(右侧)或"less"(左侧)
method为计算方法,包括"pearson"、"kendall"和"spearman’"三种
> cor.test(x1,x2)
Pearson's product-moment correlation
data: x1 and x2
t = 10.743, df = 10, p-value = 8.21e-07
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.8574875 0.9888163
sample estimates:
cor
0.9593031
由于p<0.05,于是在显著性水平a=0.05上接受H1,可认
为该人群身高与体重呈现正的线性关系。
注:相关系数的显著性与自由度有关,如n=3,n-2=1时,虽然r=-0.9070,却为不显著;当n=400时,即使r=-0.1000,亦为显著。因此不能只看r的值就下结论,还需看其样本量的大小。
二.一元线性回归分析的R计算
直线方程的模型为:y=a+bx
式中,y为因变量y的估计值,x为自变量的实际值,a、b为待估参数。
其几何意义是:a是直线方程的截距,b是斜率。
其经济意义是:a是当x为0时y的估计值,b是当x每增加一个单位时y增加的数量。b也叫回归系数。
建立直线回归方程:得到回归方程:y=-140.364+1.159x
> b=lxy(x1,x2)/lxy(x1,x1)
> a=mean(x2)-b*mean(x1)
> c(a=a,b=b)
a b
-140.36436 1.15906
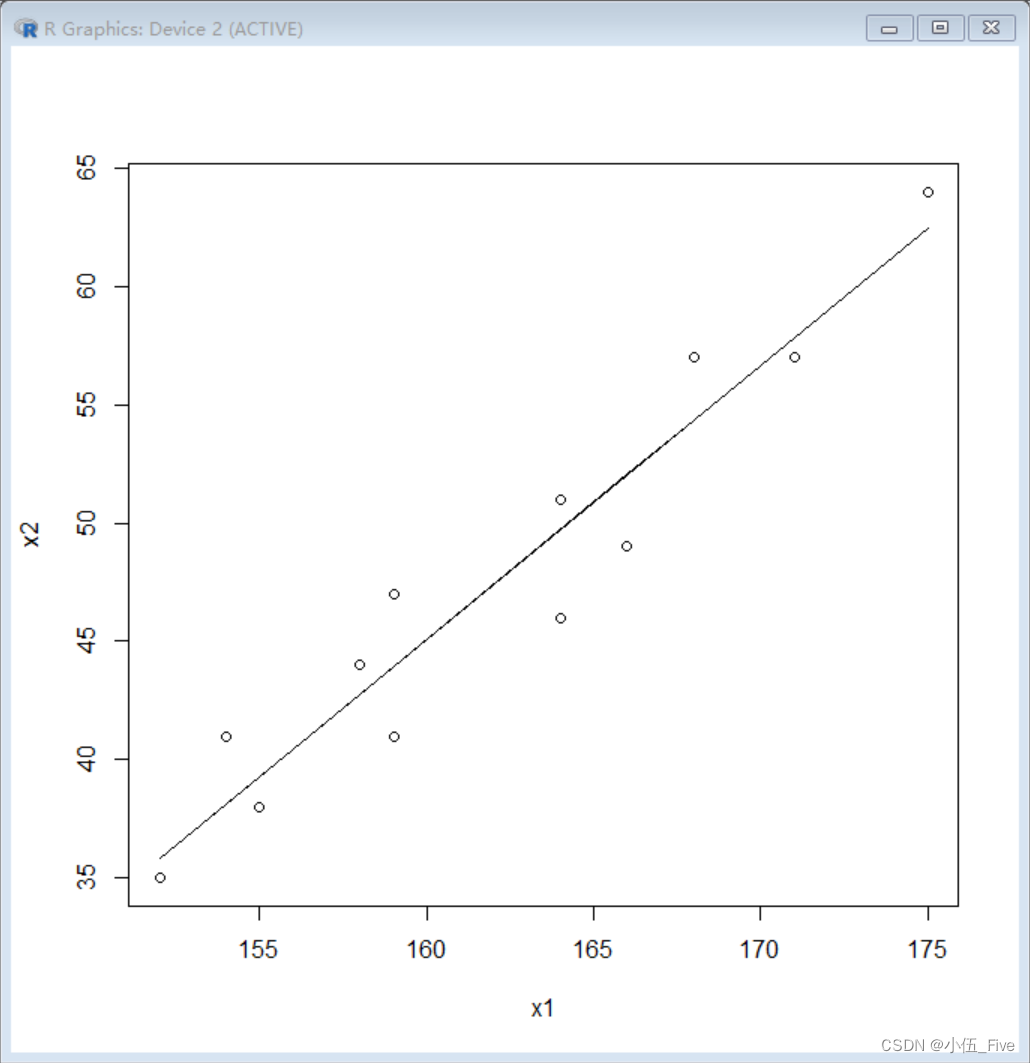
建立回归方程,作出回归直线
> plot(x1,x2);lines(x1,a+b*x1)
三、回归系数的假设检验
1.方差分析
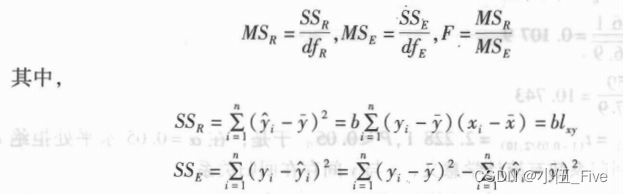
> SST=lxy(x2,x2)
> SSR=b*lxy(x1,x2)
> SSE=SST-SSR
> MSR=SSR/1
> MSE=SSE/(n-2)
> F=MSR/MSE
> c(SST=SST,SSR=SSR,SSE=SSE,MSR=MSR,MSE=MSE,F=F)
SST SSR SSE MSR MSE F
813.000000 748.173425 64.826575 748.173425 6.482657 115.411531
2.t检验

> sy.x=sqrt(MSE)
> sb=sy.x/sqrt(lxy(x1,x1))
> t=b/sb
> ta=qt(1-0.05/2,n-2)
> c(sy.x=sy.x,sb=sb,t=t,ta=ta)
sy.x sb t ta
2.5461063 0.1078901 10.7429759 2.2281389
R语言自身的拟合线性模型函数
lm()
lm(formula,…)
formula为模型公式,如y~x
例:财政收入与税收的关系探究
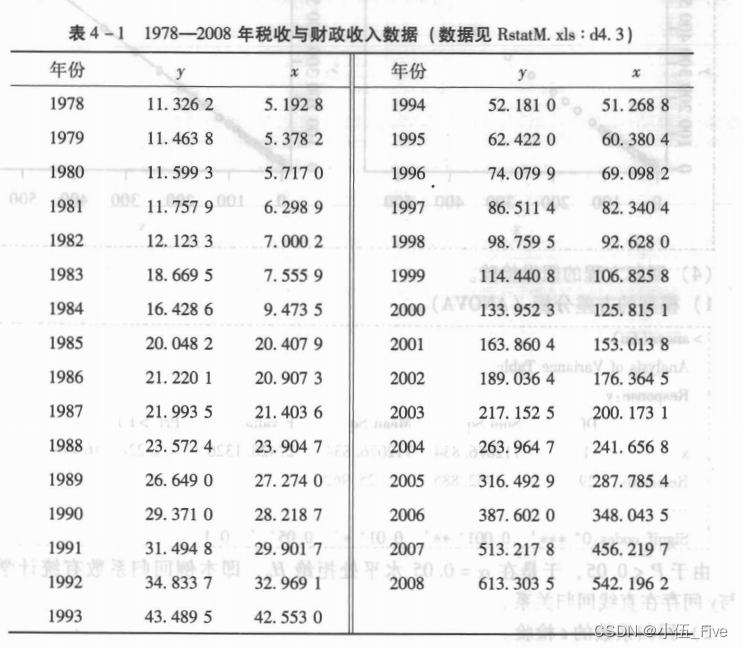
> yx=read.table("clipboard",header=T)
> attach(yx)
> fm=lm(y~x)
> fm
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
-1.197 1.116
得到回归方程:y=-1.197+1.116x
接着作回归直线:
> plot(x,y);abline(fm)
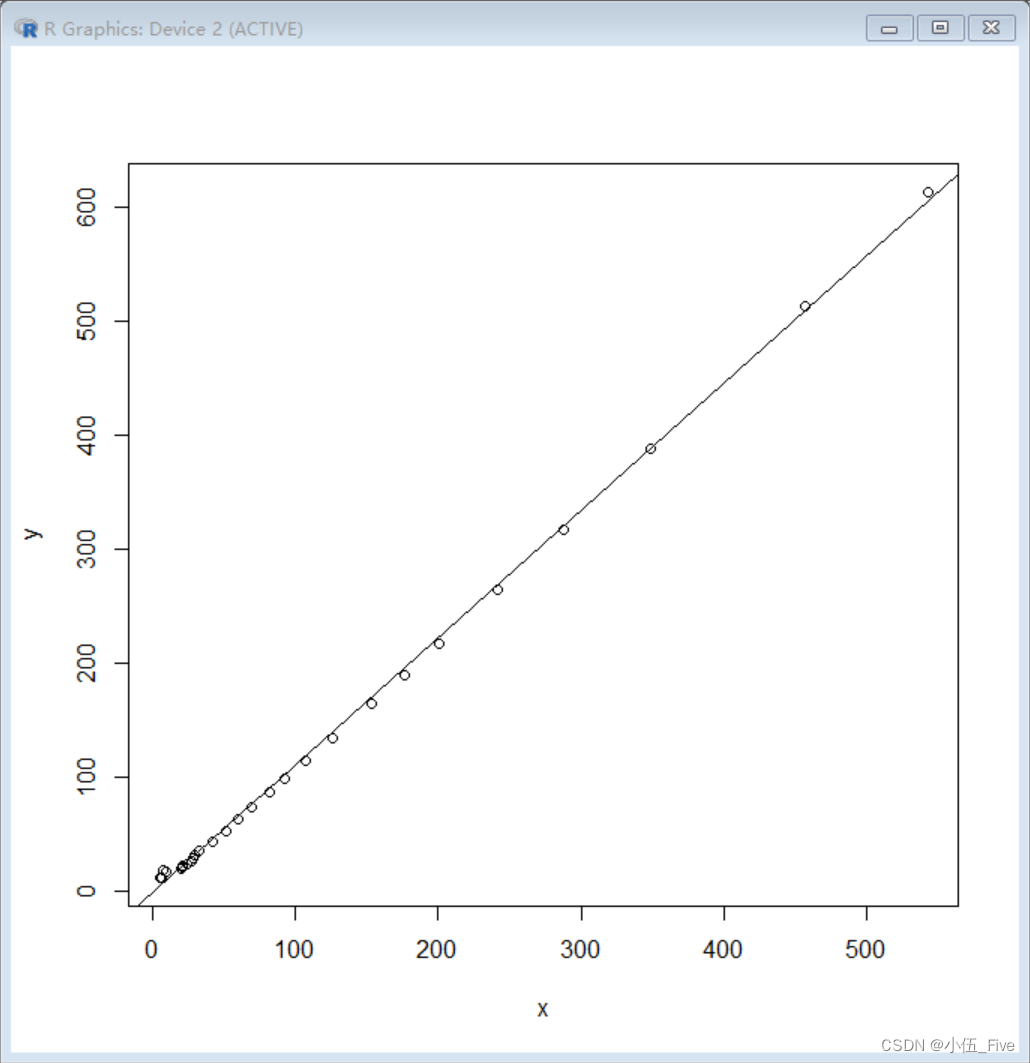
作回归方程的假设检验
1)模型的方差分析(ANOVA)
> anova(fm)
Analysis of Variance Table
Response: y
Df Sum Sq Mean Sq F value Pr(>F)
x 1 712077 712077 27427 < 2.2e-16 ***
Residuals 29 753 26
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
P<0.05,x与y间存在直线回归关系
2)回归系数的t检验
> summary(fm)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-6.631 -3.692 -1.535 5.338 11.432
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.19660 1.16126 -1.03 0.311
x 1.11623 0.00674 165.61 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 5.095 on 29 degrees of freedom
Multiple R-squared: 0.9989, Adjusted R-squared: 0.9989
F-statistic: 2.743e+04 on 1 and 29 DF, p-value: < 2.2e-16
由于P<0.05,则x与y间存在回归关系
总结
本小节主要学习了线性相关系数及一元线性回归分析,重点讨论了假设检验等方法过程,继续加油,下节就是多元线性回归分析啦