🎁个人主页:我们的五年
🔍系列专栏:C语言基本概念
🌷追光的人,终会万丈光芒

目录
🏝1.int的基本概念:
空间大小:
有符号类型的表示形式:
🏝2.原码、反码、补码
🏝3.观察+0和-0:
🏝4.注意:
前言:
还记得那个刚刚学习C语言,老师给我们讲课的时候,我就稍微了解一下为什么int类型的数据,负数可以表示到-2³¹,而正数只能表示到2³¹-1。
现在也是有时间让我好好写篇文章研究研究它的来龙去脉。
🏝1.int的基本概念:
空间大小:
●int表示的有符号的整形,int占用4个字节。一个字节是八个比特位,也就是int占用32个比特位,数据在计算机里面存储都是以二进制的形式存储的,并且是以二进制的补码进行存储。
以二进制的原码进行打印。
有符号类型的表示形式:
●有符号的类型,用第一位来表示符号位,1代表负数,0代表正数,其他31位就是用,表示数值,比特位只能放1和0。
1的二进制表示形式:0000 0000 | 0000 0000 | 0000 0000 | 0000 0001
-1的二进制表示形式: 1000 0000 | 0000 0000 | 0000 0000 | 0000 0001
所以当出符号位以外,其他的都存1时,可以表示最大的数。
即正数最大为:
0111 1111 | 1111 1111 | 1111 1111 | 1111 1111=2³¹-1=2147483647
当符号为1时,此时为表示为-2³¹+1=-2147483647
此时我们看,如果这样来看,好像int只能表示-2³¹+1~2³¹-1呀,为什么还能表示到-2³¹呢?
🏝2.原码、反码、补码
我们输入的数,一开始是原码,要变成补码以后,才能存储的计算机中,打印的是原码。
正数的原码、反码、补码都相同。
负数从原码到反码是符号位不变,其他的取反,这里的取反就是,0变成1,1变成0,因为二进制里面只有0和1.
负数从反码到补码:直接+1
-1的原码:1000 0000 | 0000 0000 | 0000 0000 | 0000 0001
-1的反码:1111 1111 | 1111 1111 | 1111 1111 | 1111 1110
-1的补码:1111 1111 | 1111 1111 | 1111 1111 | 1111 1111
-1补码的16进制形式:ff ff ff ff
观察下面代码输出的值为多少?
#include<stdio.h>
int main()
{
int a = 0X80000000;
int b = 0X80000001;
int c = 0Xffffffff;
printf("%d\n%d\n%d\n", a, b, c);
return 0;
}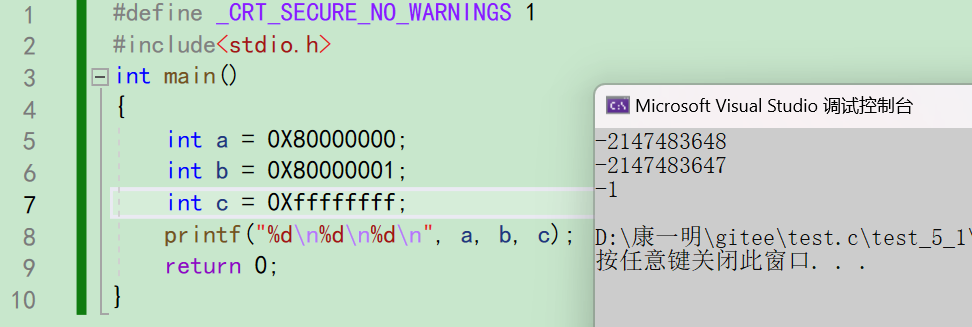
对于上面的这个,我的理解是,如果采用0X进行赋值,那么就直接在计算机以这种形式保存下来,因为保存的是补码,负数要转为原码以后,才能打印。
当补码为-0的时候,原码表示为-2³¹。
当补码为-1的时候,原码表示为-2³¹+1。
当补码为1111 1111 | 1111 1111 | 1111 1111 | 1111 1111,原码为-1.
🏝3.观察+0和-0:
+0:0000 0000 | 0000 0000 | 0000 0000 | 0000 0000
-0:1000 0000 | 0000 0000 | 0000 0000 | 0000 0000
+0和-0,都是表示0,那么我们就没有必要用两个数共同来表示0,我们用+0表示0,用-0取表示其他的数,上面我们也发现,-0其实表示的是-2³¹,所以这也是一种规定,可以让我们对资源有一个更充分的利用。
🏝4.注意:
我们来看一下这个东西:
#include<stdio.h>
int main()
{
int a = -2147483648;
a = -a;
printf("%d\n", a);
return 0;
}这里的a就是-2³¹,我们可以直接把它转为正数,然后打印出来吗?
答案是不可以的,因为如果转为正数,放到int里面,int类型是存不下的,int只能存2³¹-1。所以要这么做的话,我们是能把它存到long 类型,或者long long类型。