统计特征是描述数据集中值的一组量，通常用于了解数据的分布、集中趋势和变异程度。常见的统计特征包括均值、中位数、众数、标准差、方差等。下面会详细解释每个统计特征，并给出相应的Python代码。

        1、均值（Mean）：所有数据值的平均值。计算公式为：

        

        其中 𝑥𝑖是第 𝑖个数据值，是数据的总数。

def mean(data):
    return sum(data) / len(data)

# Example
data = [1, 2, 3, 4, 5]
print("Mean:", mean(data))

        2、中位数（Median）：将数据排序后位于中间位置的值，如果数据个数为奇数，则中位数为中间的值；如果为偶数，则为中间两个数的平均值。

def median(data):
    sorted_data = sorted(data)
    n = len(sorted_data)
    mid = n // 2
    if n % 2 == 0:
        return (sorted_data[mid - 1] + sorted_data[mid]) / 2
    else:
        return sorted_data[mid]

# Example
data = [1, 2, 3, 4, 5]
print("Median:", median(data))

        3、众数（Mode）：数据集中出现频率最高的值。一个数据集可能有一个或多个众数。

from collections import Counter

def mode(data):
    counts = Counter(data)
    max_count = max(counts.values())
    mode = [k for k, v in counts.items() if v == max_count]
    return mode

# Example
data = [1, 2, 2, 3, 4, 4, 4, 5]
print("Mode:", mode(data))

        4、标准差（Standard Deviation）：衡量数据集合中数据值的分散程度，标准差越大表示数据越分散。公式：

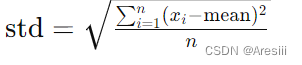
import math

def standard_deviation(data):
    m = mean(data)
    variance = sum((x - m) ** 2 for x in data) / len(data)
    return math.sqrt(variance)

# Example
data = [1, 2, 3, 4, 5]
print("Standard Deviation:", standard_deviation(data))

     5、方差（Variance）：标准差的平方，表示数据分散程度的一个度量。

def variance(data):
    m = mean(data)
    return sum((x - m) ** 2 for x in data) / len(data)

# Example
data = [1, 2, 3, 4, 5]
print("Variance:", variance(data))

        这些是常见的统计特征及其相应的Python实现。在实际应用中，可以根据数据的特点选择合适的统计特征来描述和分析数据。