1、分治算法
分治(divide and conquer),全称分而治之,是一种非常重要且常见的算法策略。分治通常基于递归实现,包括“分”和“治”两个步骤。
- 分(划分阶段):递归地将原问题分解为两个或多个子问题,直至到达最小子问题时终止。
- 治(合并阶段):从已知解的最小子问题开始,从底至顶地将子问题的解进行合并,从而构建出原问题的解。
一个问题是否适合使用分治解决,通常可以参考以下几个判断依据。
- 问题可以分解:原问题可以分解成规模更小、类似的子问题,以及能够以相同方式递归地进行划分。
- 子问题是独立的:子问题之间没有重叠,互不依赖,可以独立解决。
- 子问题的解可以合并:原问题的解通过合并子问题的解得来。
分治不仅可以有效地解决算法问题,往往还可以提升算法效率。在排序算法中,快速排序、归并排序、堆排序相较于选择、冒泡、插入排序更快,就是因为它们应用了分治策略。
2、汉诺塔问题
2.1 传说
大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。 简化后类似如下:
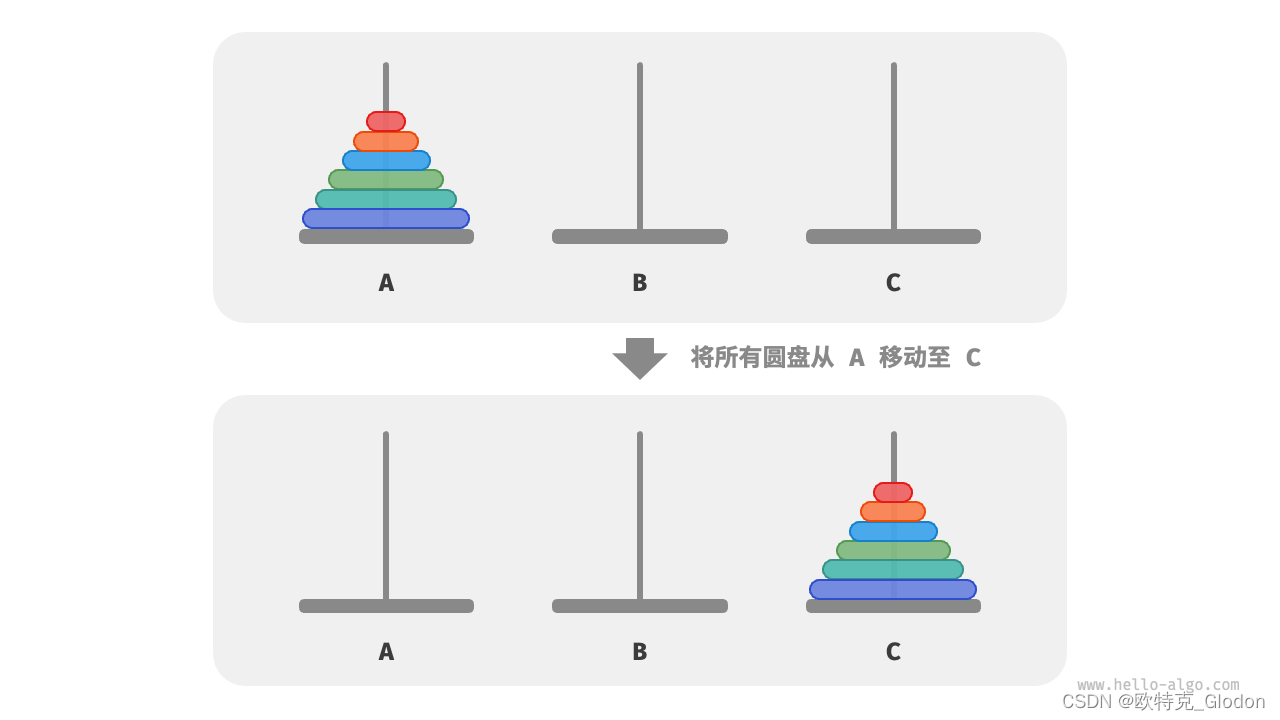
2.2 分治策略
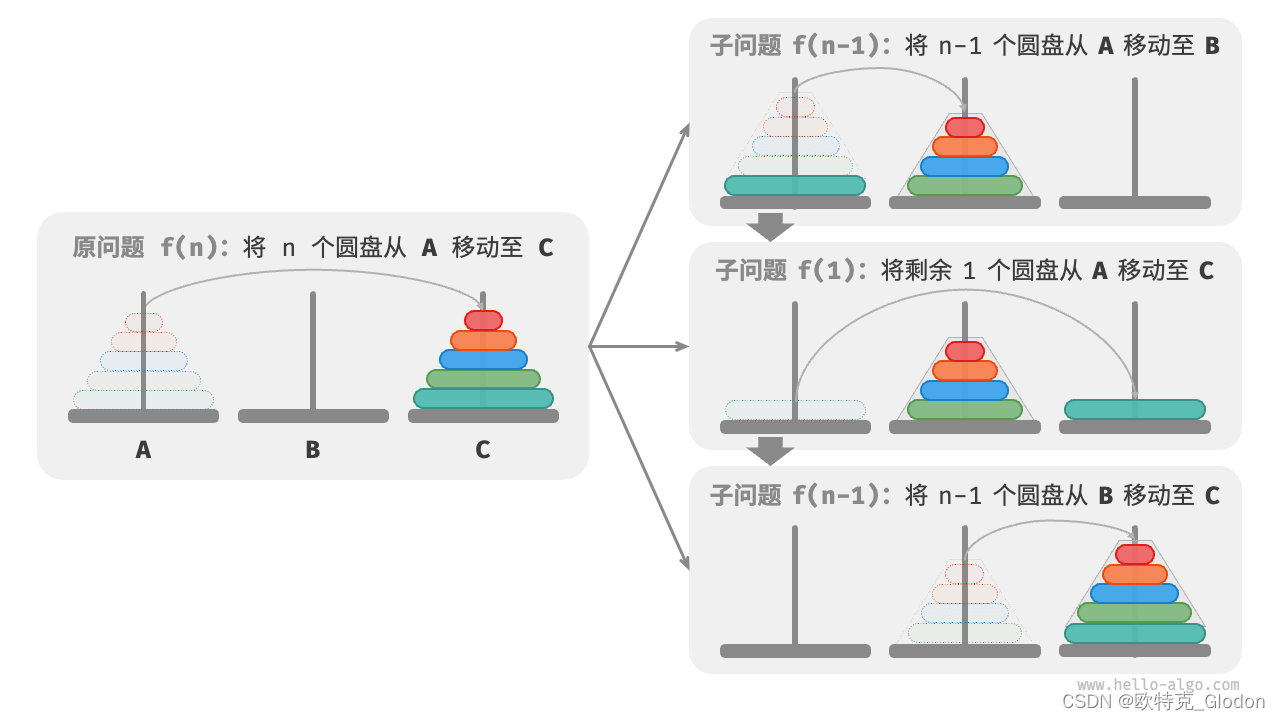
解决汉诺塔问题的分治策略:将原问题f(n)划分为两个子问题f(n-1)和一个子问题f(1),并按照以下顺序解决这三个子问题。
- 将n-1个圆盘借助 C 从 A 移至 B 。
- 将剩余1个圆盘从 A 直接移至 C 。
- 将n-1个圆盘借助 A 从 B 移至 C 。
对于这两个子问题 f(n-1),可以通过相同的方式进行递归划分,直至达到最小子问题 f(1)。而f(1)的解是已知的,只需一次移动操作即可。
2.3 代码实现
/* 求解汉诺塔问题 f(i) */
/* 移动一个圆盘 */
void move(vector<int>& src, vector<int>& tar)
{
// 从 srcA 顶部拿出一个圆盘
int pan = src.back();
src.pop_back();
// 将圆盘放入 tarC 顶部
tar.push_back(pan);
}
void dfs(int nSize, vector<int>& srcA, vector<int>& bufB, vector<int>& tarC,int& nMoveTimes)
{
// 若 srcA 只剩下一个圆盘,则直接将其移到 tarC
if (nSize == 1)
{
nMoveTimes++;
move(srcA, tarC);
return;
}
// 子问题 f(i-1) :将 srcA 顶部 i-1 个圆盘借助 tarC 移到 bufB
dfs(nSize - 1, srcA, tarC, bufB, nMoveTimes);
// 子问题 f(1) :将 srcA 剩余一个圆盘移到 tarC
move(srcA, tarC);
// 子问题 f(i-1) :将 bufB 顶部 i-1 个圆盘借助 srcA 移到 tarC
dfs(nSize - 1, bufB, srcA, tarC, nMoveTimes);
}
void solveHanota(vector<int>& A, vector<int>& B, vector<int>& C, int& nMoveTimes)
{
int nSize = A.size();
// 将 A 顶部 n 个圆盘借助 B 移到 C
dfs(nSize, A, B, C, nMoveTimes);
}
int main()
{
int nObject = 25;
vector<int> vecObject;
for (int i = nObject; i > 0; i--)
{
vecObject.push_back(i);
}
int nMoveTimes = 0;
vector<int> objectB;
vector<int> objectC;
solveHanota(vecObject, objectB, objectC, nMoveTimes);
std::cout << "放置圆盘" << nObject << "个,共计需要移动" << nMoveTimes << "次!" << endl;
return 0;
}
放置圆盘25个,共计需要移动16777216次!
2.4 代码漏洞
当盘子数量为64的话,一共需要移动约1800亿亿步(18,446,744,073,709,551,615),才能最终完成整个过程。即使借助于计算机,假设计算机每秒能够移动100万步,那么约需要18万亿秒,即58万年。将计算机的速度再提高1000倍,即每秒10亿步,也需要584年才能够完成。所以上述解法无法处理大数据量问题
3、递归导致栈溢出
递归算法在数学问题上会经常出现,但运用不当会出问题。有的是运算时间太长如上面的汉诺塔问题,有的则是栈溢出,例如下面代码。我们着重说一下栈溢出问题。
// 递归求和函数当n=4750会出现栈溢出问题
void Sum(int& nSum, int n)
{
if (n == 0)
{
return;
}
nSum += n;
n--;
Sum(nSum, n);
}
// 斐波那契数列 0,1,1,2,3,5,8…… 递归树 时间复杂度高 会卡死
unsigned int fib(int n)
{
if (n == 1 || n == 2)
{
return n - 1;
}
return fib(n - 2) + fib(n - 1);
}
// 阶乘 时间复杂度高 卡死
unsigned int factorialRecur(unsigned int n)
{
if (n == 0)
{
return 1;
}
int count = 0;
for (int i = 0; i < n; i++)
{
count += factorialRecur(n - 1);
}
return count;
}
3.1 为什么会栈溢出?
计算机的内存可以分为三个区域:栈区,堆区,静态区。它们在存储使用时遵循不同的规则,并且存储的内容也不同。其中栈内存速度最快但空间很小一般只有几兆M大小,而我们每一次递归时,上一次的递归程序仍然没有结束,也就是上一次递归的函数仍然占据着内存栈区的空间; 递归调用函数次数太多栈就会溢出。
3.2 解决方式
对于栈溢出的问题一般通过减少递归的层数来解决。比如下面的求和问题。
// 递归求和函数当n=4750会出现栈溢出问题
void Sum(int& nSum, int n)
{
if (n == 0)
{
return;
}
nSum += n;
n--;
Sum(nSum, n);
}
// 迭代求和 可正常计算
unsigned int Sum(int n)
{
int nSum = 0;
for (int a = 1; a <= n; a++)
{
nSum += a;
}
return nSum;
}