背景：
本来我是想提取xml中的信息存在xlsx文件中的，网上很多说是使用QtXlsx；
于是我找了一些帖， 像：https://www.cnblogs.com/liming19680104/p/14398459.html；
大家的说法都是安装第三方库到QT中；

我因为是32位的工程所以QtXlsx其实我是没走通的；但是毕竟研究了一天，还是写一下我的总结；希望对其他人有所帮助，我的问题是32位的再编译QtXlsx代码时不会给我生成.lib文件，所以当我引入这个库调用接口就会报错；

安装步骤：

1.下载源码 https://gitcode.com/dbzhang800/QtXlsxWriter/overview?utm_source=csdn_github_accelerator&isLogin=1 我看了很多帖子，都是下的这个源码；
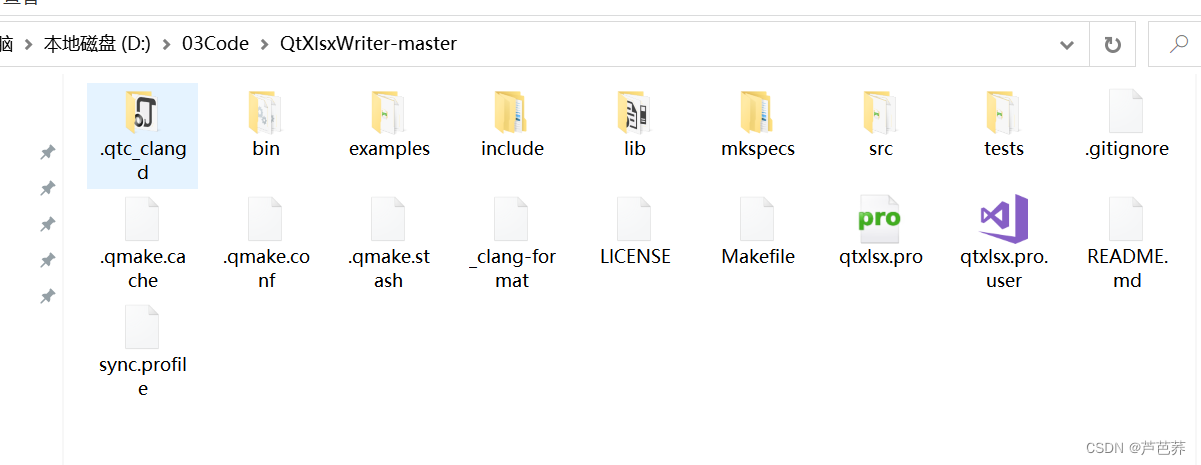
主要代码在src中，这里bin\include\lib、mkspecs都是输出文件；

2.下载perl工具ActivePerl-5.28.1.0000-MSWin32-x64-c50440fa.exe 网盘
安装perl步骤：https://blog.csdn.net/MrHHHHHH/article/details/134233707?spm=1001.2014.3001.5502
3.编译+安装插件
https://blog.csdn.net/MrHHHHHH/article/details/134233634?spm=1001.2014.3001.5506

4.QTCreator工具开发的工程：使用MinGW工具进行安装
cmd命令插件安装就是三步：
a.切换到代码src下

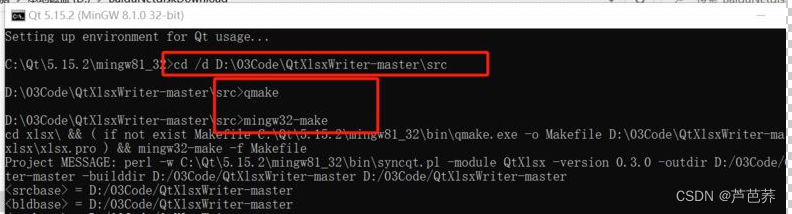
b.qmake 生成MakeFile文件

c.执行mingw32-make对Qtxlsx代码进行一个编译，这步之后会生成dll\prt\lib等文件；

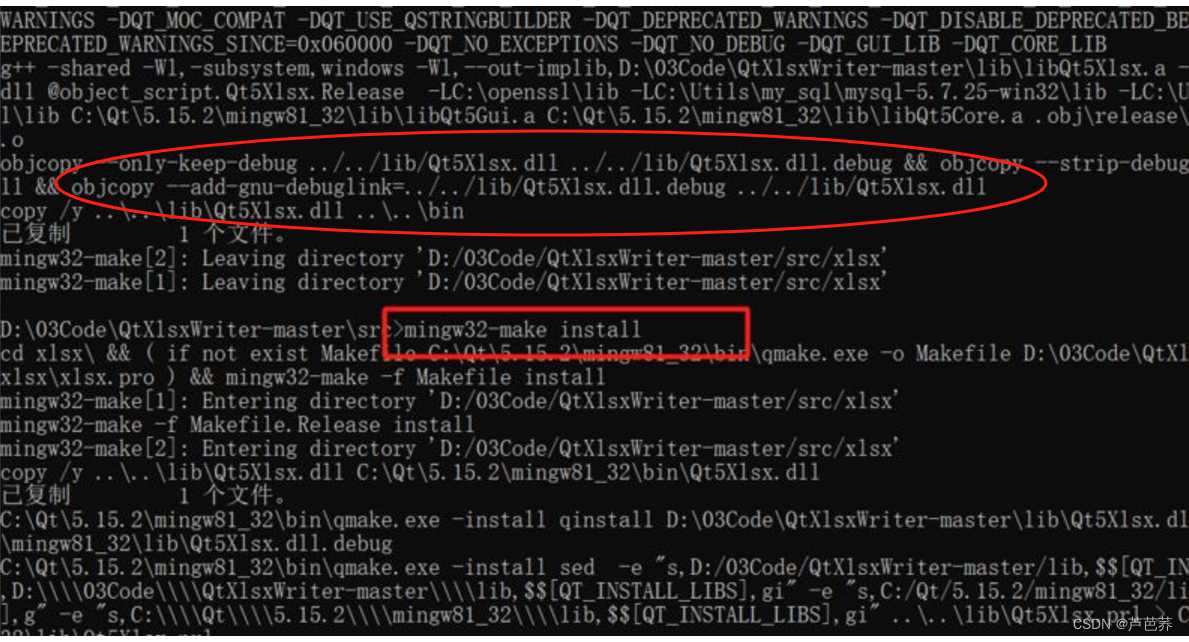
d.mingw32-make install 进行安装，主要操作实际就是拷贝编译的文件和文件等到对应QT下

主要是
D:\03Code\QtXlsxWriter-master\bin-》C:\Qt\5.15.2\mingw81_32\bin
D:\03Code\QtXlsxWriter-master\include-》C:\Qt\5.15.2\mingw81_32\include
D:\03Code\QtXlsxWriter-master\lib-》C:\Qt\5.15.2\mingw81_32\lib
D:\03Code\QtXlsxWriter-master\mkspecs\modules-inst-》C:\Qt\5.15.2\mingw81_32\mkspecs\modules

5.安装后再工程设置里可以直接加上这个模块：

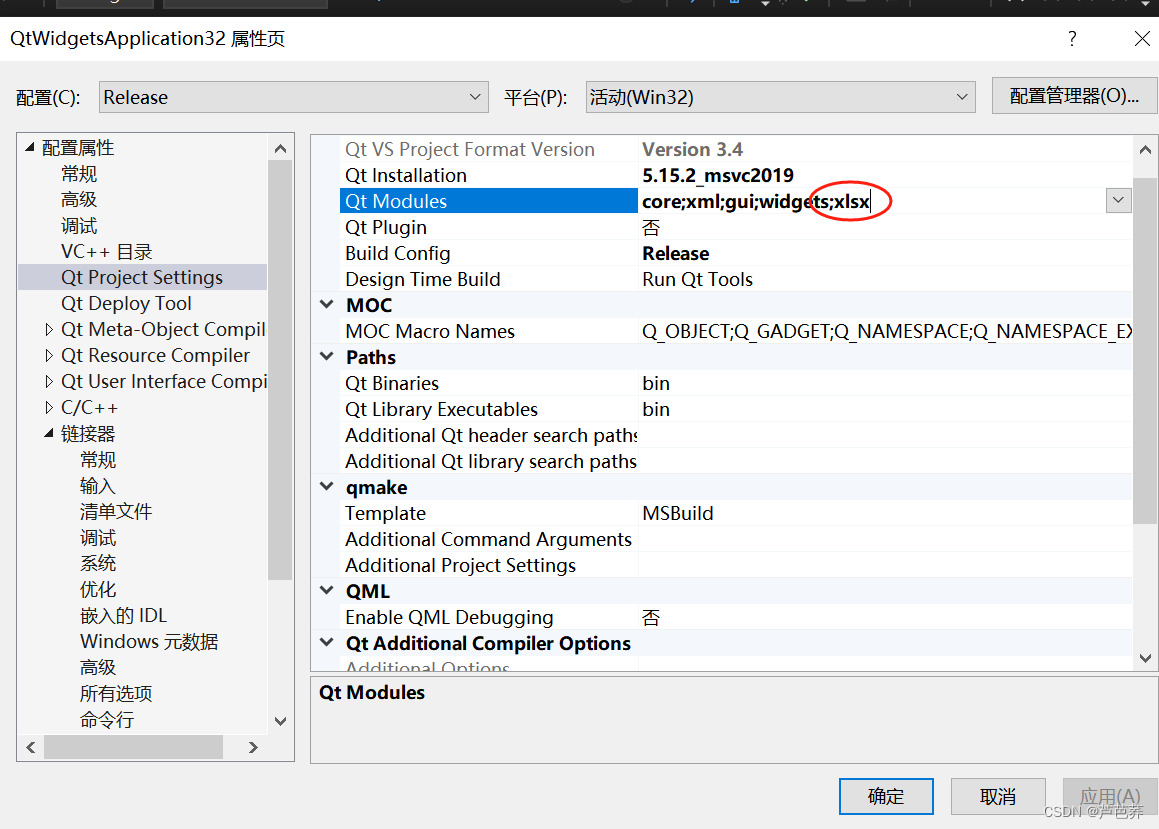
然后跟其他人写的一样 include 使用就可以了；

我的工程是VS2022开发的，所以我需要编译VS的：
按如下操作使用VS编译相应的库文件
C:\Qt\5.15.2\msvc2019\bin>qtenv2
D:\03Code\QtXlsxWriter-master\src> qmake
D:\03Code\QtXlsxWriter-master\src>nmake
D:\03Code\QtXlsxWriter-master\src> nmake install

也可以使用QtCreator进行编译；以上仅支持64位，因为32位的编完没有lib文件；

有问题欢迎指正！