一、备忘录模式概述
备忘录模式定义:又称之为快照模式(Snapshop Pattern)或者令牌模式(Token Pattern),是指在不破坏封装的前提下,捕获一个对象的内部状态,并在对象之外保存这个状态,这样我们就可以在需要的时候将该对象恢复到原先保存的状态了。(对象行为型)
备忘录模式有两个目标:
- 储存系统关键对象的重要状态;
- 维护关键对象的封装。

- 备忘录模式的优缺点:
- 优点:
- 1.将被储存的状态放在外面,不要和关键对象混在一起,这可以帮助维护内聚;
- 2.提供了容易实现的恢复能力;
- 3.保持关键对象的数据封装。
- 缺点:
- 储存和恢复状态的过程可能相当耗时。
- 优点:
- 适用环境:
- 1.需要保存历史快照的场景;
- 2.希望在对象之外保存状态,且除了自己其他对象无法访问状态的具体保存内容。
二、代码实现
备忘录模式主要有3个角色:
- 发起人(Originator)角色:负责创建一个备忘录,记录自身需要保存的状态,而且需要具备状态的回滚功能。
- 备忘录(Memento)角色:用于存储Originator角色的内部状态,且可以防止Originator以外的对象进行访问。
- 备忘录管理员(Caretaker)角色:负责存储,管理备忘录功能。且其本身应该无法对备忘录的内容进行访问。
2.1 Originator
package Memento.example;
//发起人角色
public class Originator {
private String state;
public void setState(String state) {
this.state = state;
}
public String getState() {
return state;
}
public Memento saveStateToMemento() {
return new Memento(state);
}
public void getStateFromMemento(Memento Memento) {
state = Memento.getState();
}
}2.2 Memento
package Memento.example;
//备忘录角色
public class Memento {
private String state;
public Memento(String state) {
this.state = state;
}
public String getState() {
return state;
}
}
2.3 Caretaker
package Memento.example;
//备忘录管理员
import java.util.ArrayList;
import java.util.List;
public class CareTaker {
private List<Memento> mementoList = new ArrayList<Memento>();
public void add(Memento state){
mementoList.add(state);
}
public Memento get(int index){
return mementoList.get(index);
}
}2.4 客户端
package Memento.example;
public class Client {
public static void main(String[] args) {
// TODO Auto-generated method stub
Originator originator = new Originator();
CareTaker careTaker = new CareTaker();
originator.setState("State #1");
originator.setState("State #2");
careTaker.add(originator.saveStateToMemento());
originator.setState("State #3");
careTaker.add(originator.saveStateToMemento());
originator.setState("State #4");
System.out.println("Current State: " + originator.getState());
originator.getStateFromMemento(careTaker.get(0));
System.out.println("First saved State: " + originator.getState());
originator.getStateFromMemento(careTaker.get(1));
System.out.println("Second saved State: " + originator.getState());
}
}
2.5 UML图
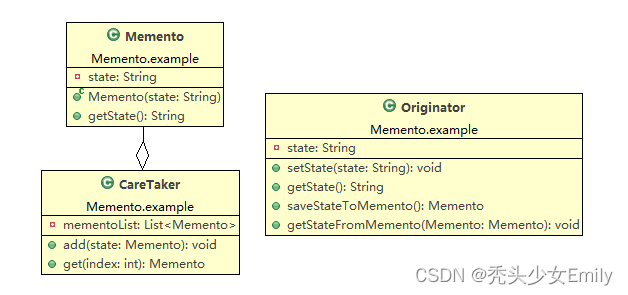
三、代码结构图






![制造企业如何打造客户服务核心竞争力?[AMT企源典型案例]](https://img-blog.csdnimg.cn/direct/5292314e9dbb41c9a5151a991c653594.jpeg)